Result of the Month

In this study, we revisit the classical problem of identifying outlier sequences from a large set of sequences when neither the typical distribution nor the outlier distribution is known a priori (universal setting). Assuming that the number of sequences grow faster than the sequence lengths, we introduce and analyze two simple yet powerful test statistics — mean‐based and median‐based estimators — that are computationally tractable and whose errors decrease exponentially with the sequence length. If the number of outliers grows sublinearly with the total number of sequences, a mean-based test that estimates the typical distribution by averaging the empirical distributions across all sequences achieves the same error exponent as the maximum likelihood test that has full knowledge of the typical and outlier distribution. If outliers comprise a constant fraction of sequences, the mean estimate becomes biased. We show that a median-based test — using the component-wise median to estimate the...
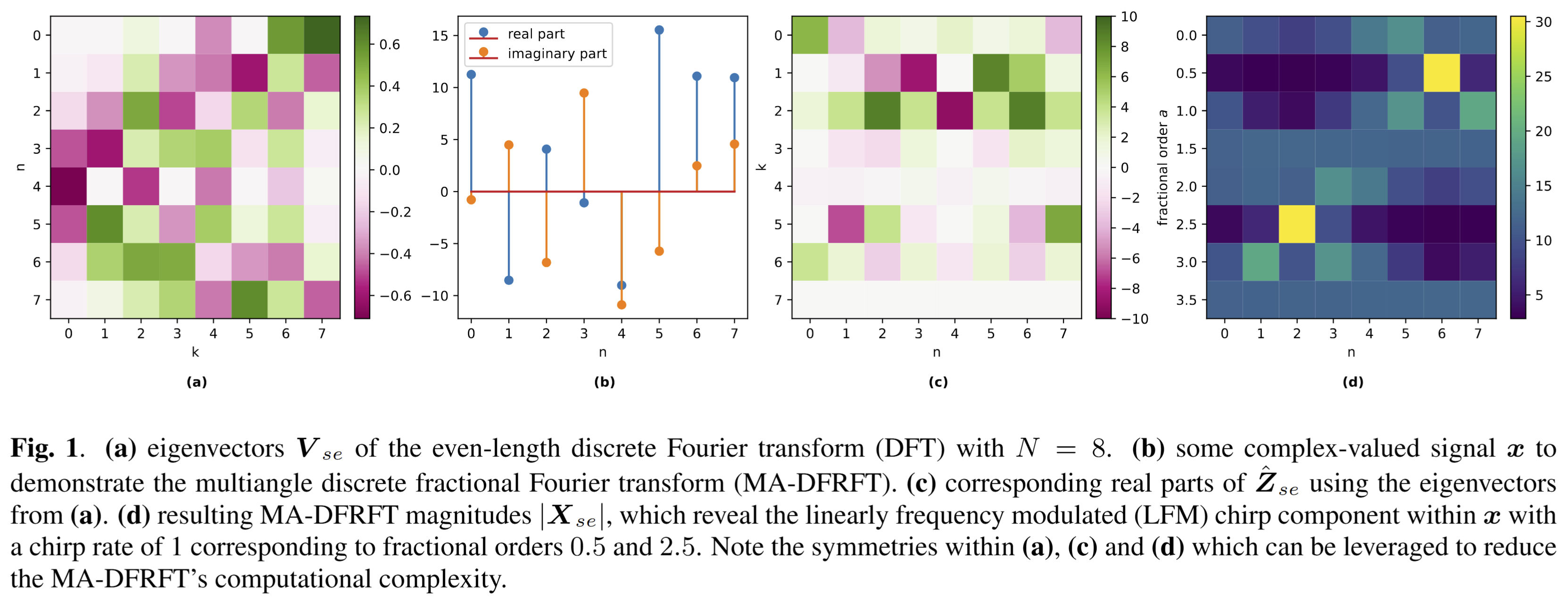
Fractional transforms such as the discrete fractional Fourier transform (DFRFT) are important tools in digital signal processing, as they are used for data compression, cryptography and watermarking, linearly frequency modulated (LFM) chirp estimation, processing optical systems, among other applications. Many of these applications require computing multiple transforms of different fractional orders; in the context of interfered radar signals, for instance, DFRFTs of different fractional orders pulse-compress LFM chirp interferences with different chirp rates, enabling their mitigation. The multiangle centered discrete fractional Fourier transform (MA-CDFRFT, Vargas-Rubio & Santhanam, IEEE SPL 12(4):273-276, 2005) utilizes FFTs to efficiently compute the CDFRFT in parallel for multiple fractional orders. In this work, we generalize the MA-CDFRFT to arbitrary M-periodic transforms; more concretely, we reduce the computational complexity of all multiangle fractional M-periodic transforms from O(N^3) to O(N^2 log N). We do this by generalizing the method by Vargas-Rubio & Santhanam to arbitrary period-lengths M, eigenvalue...
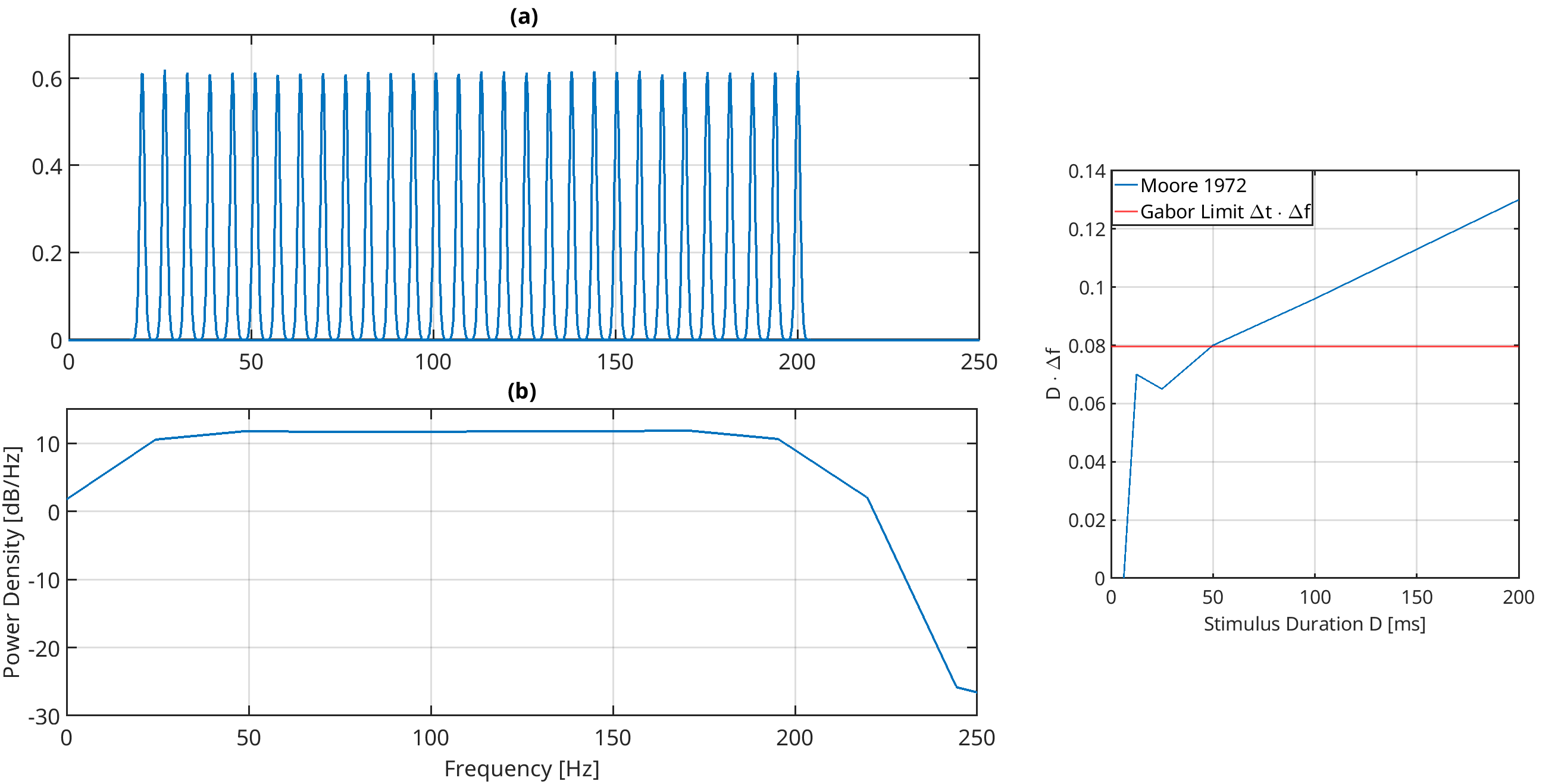
It is known that the human auditory system contains Outer Hair Cells (OHCs), which can be modeled as nonlinear oscillators. Further, it has a remarkable time-frequency resolution (Moore, 1973), with lower time-frequency resolution products below the Gabor limit (right figure). We show that this time-frequency resolution can be achieved with a Stuart-Landau Oscillator (SLO) that exhibits a subcritical Hopf bifurcation. This raises the question of whether continuously oscillating outer hair cells can exist without producing a noticeable tone (i.e., constant tinnitus)? Our results suggest yes, if these cells oscillate chaotically. When modeled as SLOs with white system noise, every cell exhibits narrowband chaos (top left figure), with the mean equal to the cell’s characteristic frequency. By looking at the summed output of an ensemble of OHCs, the power spectrum density becomes constant, indicating a Gaussian process rather than multiple pure tones (bottom left figure). This suggests that narrowband chaos is...

Ensuring trustworthiness in machine learning—by balancing utility, fairness, and privacy—remains a critical challenge, particularly in representation learning. In this work, we investigate a family of closely related information-theoretic objectives, including information funnels and bottlenecks, designed to extract invariant representations from data. We introduce the Conditional Privacy Funnel with Side-information (CPFSI), a novel formulation within this family, applicable in both fully and semi-supervised settings. Given the intractability of these objectives, we derive neural-network-based approximations via amortized variational inference. We systematically analyze the trade-offs between utility, invariance, and representation fidelity, offering new insights into the Pareto frontiers of these methods. Our results demonstrate that CPFSI effectively balances these competing objectives and frequently outperforms existing approaches. Furthermore, we show that by intervening on sensitive attributes in CPFSI’s predictive posterior enhances fairness while maintaining predictive performance. Our paper is published open-access in Machine Learning (Springer).
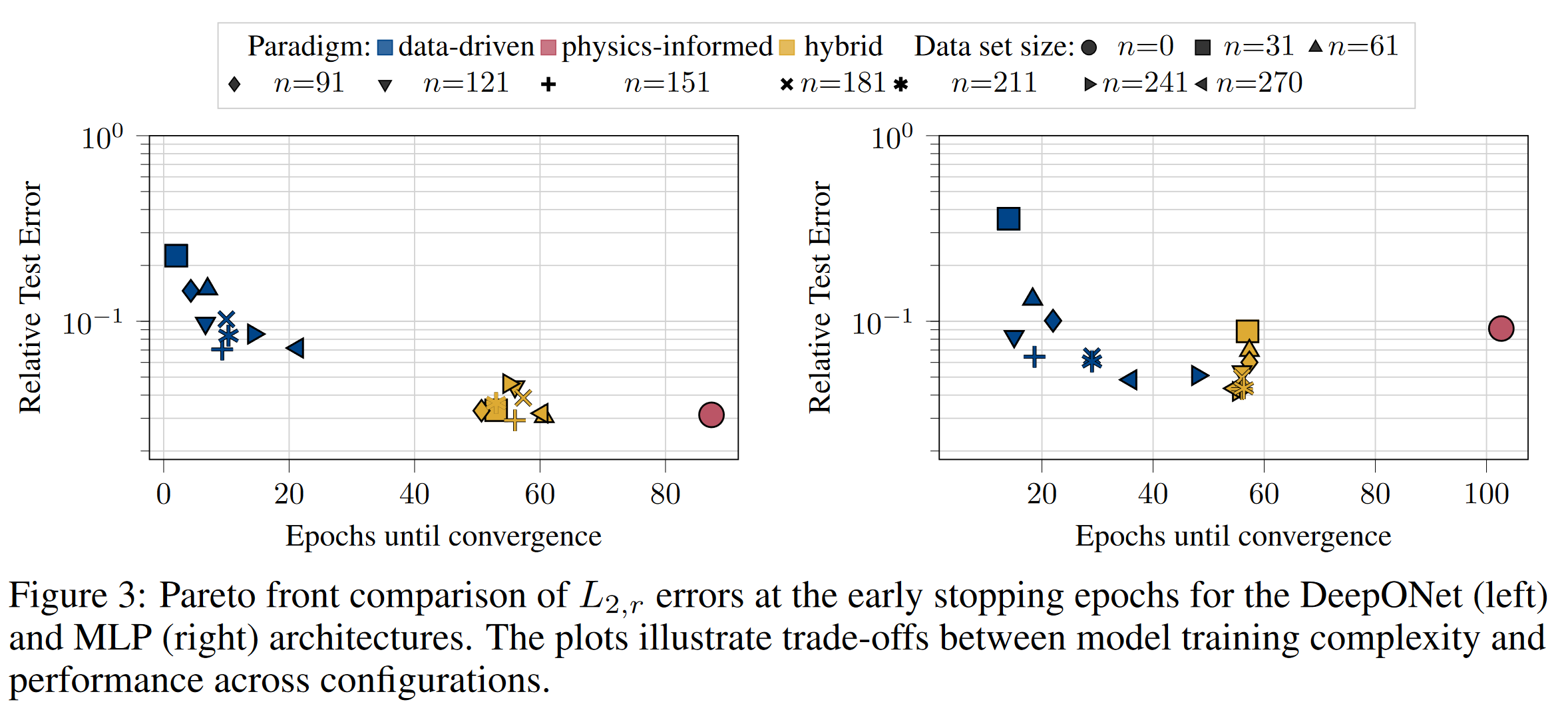
Operator networks have emerged as promising surrogate models, replacing computationally expensive numerical solvers for differential equations. Beyond achieving competitive accuracy with traditional solvers, the practical viability of this approach greatly depends on its training cost, which is comprised of ground truth data acquisition and network optimization. Physics-informed machine learning seeks to reduce reliance on labeled data by embedding the governing differential equations into the loss function; however, such models are often very challenging to train using physics constraints alone. In this work, we study how varying amounts of labeled data and architectural choices affect convergence and final performance in operator learning. Our results show that incorporating training data into a physics-informed training regime can significantly reduce training time. However, this effect does not scale with the amount of data used. Conversely, adding physics-based residuals can substantially enhance performance, if the network architecture is well-suited to exploit the underlying physical behavior....

Voice disorders, such as dysphonia or speech produced using an electro-larynx, often result in reduced intelligibility and unnatural prosody and speech quality. This paper investigates the potential of modern voice conversion (VC) technologies to restore healthy-sounding speech from pathological inputs. Four state-of-the-art VC models (FreeVC, QuickVC, LLVC, and XVC) were fine-tuned on Austrian-German datasets and evaluated using both objective and subjective measures. Results show substantial improvements in perceived naturalness, intelligibility, and vocal health, with listener preference scores exceeding those of the original pathological speech by up to 200 %. The study employs large-scale listening tests and quantitative analyses to assess intelligibility, rhythm, perceived vocal quality and preference ratings across 93 participants. The best-performing models (QuickVC, FreeVC, and XVC) consistently improved the naturalness and healthiness of the converted voices, while LLVC, although capable of real-time processing on CPUs, showed limited synthesis quality. Spectral analyses confirm that VC restores formant structure and...
Human communication is a remarkably coordinated activity. Successful interaction not only relies on the words themselves, but also on how these words are said, on subtle cues and fine-grained timing between conversational partners. Speakers continuously adjust to each other in real time, relying not only on linguistic content but also on prosody, gestures and context. This dynamic behavior is especially evident in spontaneous conversation, where speakers rarely plan their turns in advance but instead co-construct utterances on-the-fly and in conjunction with their interlocutors. Understanding how this coordination unfolds, particularly in the area of turn-taking, remains a central challenge for speech scientists and technologists aiming to understand and model human speech processing in spontaneous human conversation. This paper explores backchannels, short listener responses such as “mhm”, which play an important role in managing turn-taking and grounding in spontaneous conversation. The study investigates if and when backchannels occur by taking into account...
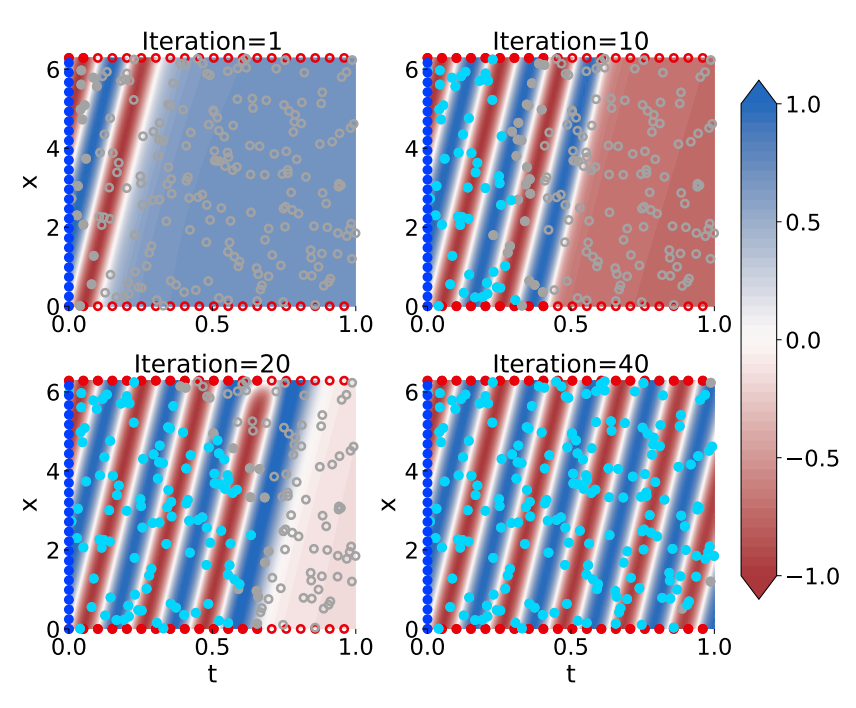
Physics-informed neural networks (PINNs) are known to have poor training convergence if they are used to solve boundary value problems, i.e., if they should learn the solution to a partial differential equation given only initial and boundary conditions. Previous work has shown that training is more stable if the computational domain – the extent of the space and time coordinates for which the PDE should be solved – is small. As a consequence, a series of domain decomposition and collocation point sampling methods were proposed to improve training convergence. Specifically, Haitsiukevich and Ilin (2023) proposed an ensemble approach that extends the active training domain of each PINN based on i) ensemble consensus and ii) vicinity to (pseudo-)labeled points, thus ensuring that the information from the initial condition successfully propagates to the interior of the computational domain. In this work with Kevin Innerebner and Franz Rohrhofer, we replaced the ensemble by...
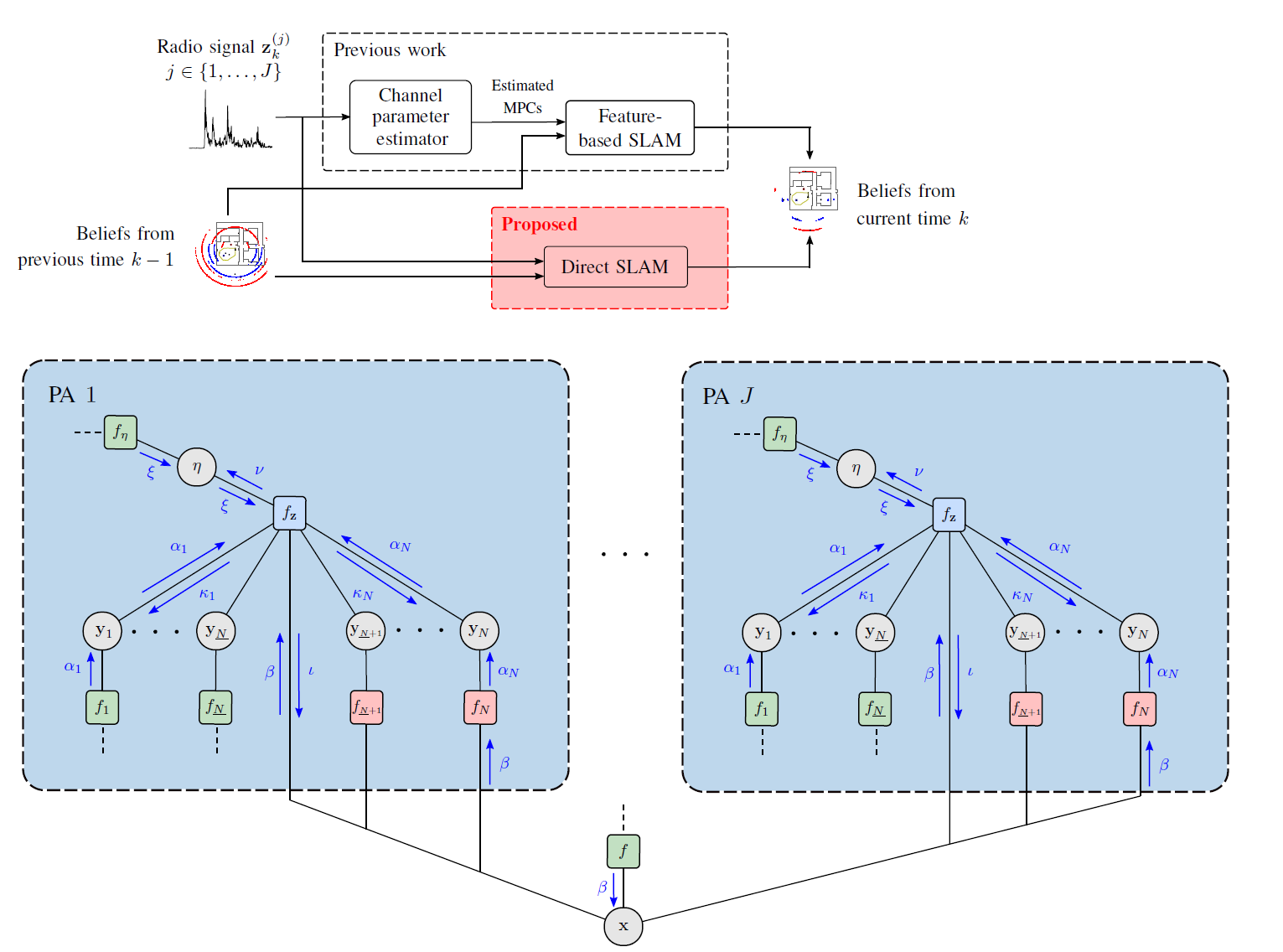
Localizing users and mapping the environment using radio signals is a key task in emerging applications such as reliable, low-latency communications, location-aware security, and safety-critical navigation. Recently introduced multipath-based simultaneous localization and mapping (MP-SLAM) can jointly localize a mobile agent (i.e., the user) and the reflective surfaces (such as walls) in radio frequency (RF) environments with convex geometries. Most existing MP-SLAM methods assume that map features and their corresponding RF propagation paths are statistically independent. These existing methods neglect inherent dependencies that arise when a single reflective surface contributes to different propagation paths or when an agent communicates with more than one base station (BS). In our paper [1], we propose a Bayesian MP-SLAM method for distributed MIMO systems that addresses this limitation. In particular, we make use of amplitude statistics to establish adaptive time-varying detection probabilities. Based on the resulting “soft” ray-tracing strategy, our method can fuse information across...
Extremely large-scale antenna array (ELAA) systems emerge as a promising technology in beyond 5G and 6G wireless networks to support the deployment of distributed architectures. This paper explores the use of ELAAs to enable joint localization, synchronization and mapping in sub-6 GHz uplink channels, capitalizing on the near-field effects of phase-coherent distributedm arrays. We focus on a scenario where a single-antenna user equipment (UE) communicates with a network of access points (APs) distributed in an indoor environment, considering both specular reflections from walls and scattering from objects. The UE is assumed to be unsynchronized to the network, while the APs can be timeand phase-synchronized to each other. We formulate the problem of joint estimation of location, clock offset and phase offset of the UE, and the locations of scattering points (SPs) (i.e., mapping). Through comprehensive Fisher information analysis, we assess the impact of bandwidth, AP array size, wall reflections, SPs...
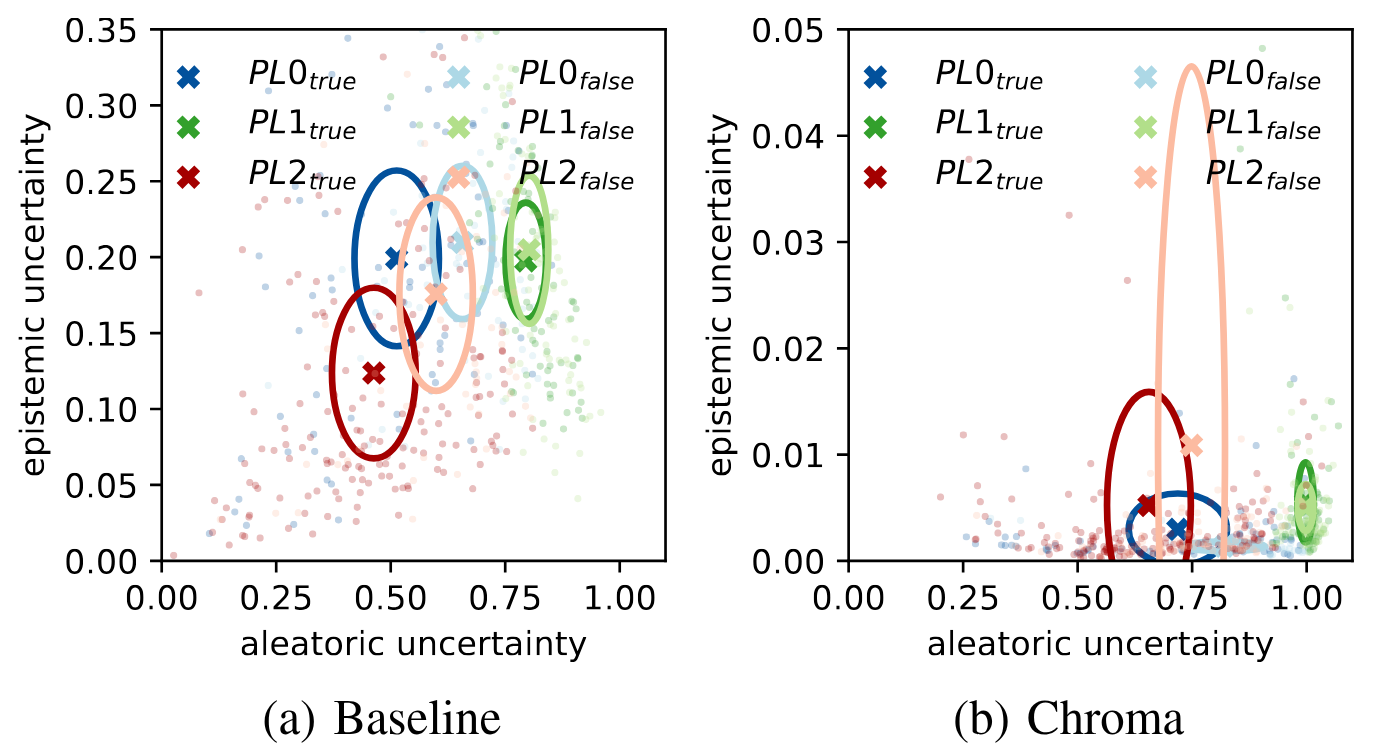
This paper presents methods for prominence classification in conversational speech. Most existing tools rely on prosodic features extracted at syllable- or phone-level, performing well on read speech. This is not the case for conversational speech, where the quality of automatic segmentation is significantly worse. We introduce entropy-based chroma features, requiring only word-level segmentations. They perform equally well as a random forest classifier with prosodic features (requiring phone-level segmentation), with accuracies in the range of the human inter-rater agreement. We further use Bayesian deep learning to quantify the epistemic and aleatoric uncertainty of the prediction for prosodic and chroma features. Whereas the aleatoric uncertainty is, as expected, consistent with inter-rater agreement and similarly high for both feature sets, the epistemic uncertainty is lower for the classifier based on chroma features, indicating higher classification consistency across the corpus.
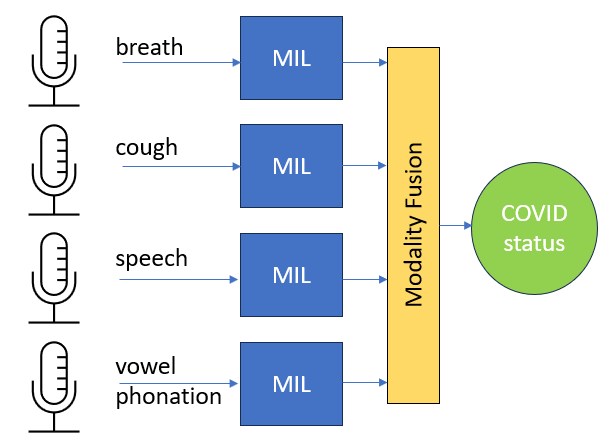
In the COVID-19 pandemic, a rigorous testing scheme was crucial. However, tests can be time-consuming and expensive. A machine learning-based diagnostic tool for audio recordings could enable widespread testing at low costs. In order to achieve comparability between such algorithms, the DiCOVA challenge was created. It is based on the Coswara dataset offering the recording categories cough, speech, breath and vowel phonation. Recording durations vary greatly, ranging from one second to over a minute. A base model is pre-trained on random, short time intervals. Subsequently, a Multiple Instance Learning (MIL) model based on self-attention is incorporated to make collective predictions for multiple time segments within each audio recording, taking advantage of longer durations. In order to compete in the fusion category of the DiCOVA challenge, we utilize a linear regression approach among other fusion methods to combine predictions from the most successful models associated with each sound modality. The application...

DER STANDARD reports on our speech group’s research and the challenges of speech recognition in the Styrian dialect. Thanks to Barbara Schuppler and her PhD students Julian Linke, Saskia Wepner and Anneliese Kelterer for their work! The STANDARD readers were excited about the article and left great comments as for example: Wir befinden uns im Jahre 2100 n.Chr. Die ganze Welt ist von den Maschinen regiert… Die ganze Welt? Nein! Ein von unbeugsamen Steirern bevölkertes Bundesland hört nicht auf, den Maschinen Widerstand zu leisten. Und das Leben ist nicht leicht für die KI, die als Besatzung in den befestigten Lagern Leibnitz, Graz, Deutschlandsberg und Leoben liegen. Trotz intensiver Anstrengungen konnte die superhumane Intelligenz die Kommunikation der Menschen nicht decodieren. Wir begleiten den Murauer Ousterix auf seinen Abenteuern, eine letzte Insel menschlicher Irrationalität zu erhalten. After completing the FWF project on the development of cross-layer models for conversational speech, their work...
Highly performing speech recognition is important for more fluent human–machine interaction (e.g., dialogue systems). Modern ASR architectures achieve human-level recognition performance on read speech but still perform sub-par on conversational speech, which arguably is or, at least, will be instrumental for human–machine interaction. Understanding the factors behind this shortcoming of modern ASR systems may suggest directions for improving them. In this work, we compare the performances of HMM- vs. transformer-based ASR architectures on a corpus of Austrian German conversational speech. Specifically, we investigate how strongly utterance length, prosody, pronunciation, and utterance complexity as measured by perplexity affect different ASR architectures. Among other findings, we observe that single-word utterances – which are characteristic of conversational speech and constitute roughly 30% of the corpus – are recognized more accurately if their F0 contour is flat; for longer utterances, the effects of the F0 contour tend to be weaker. We further find that...
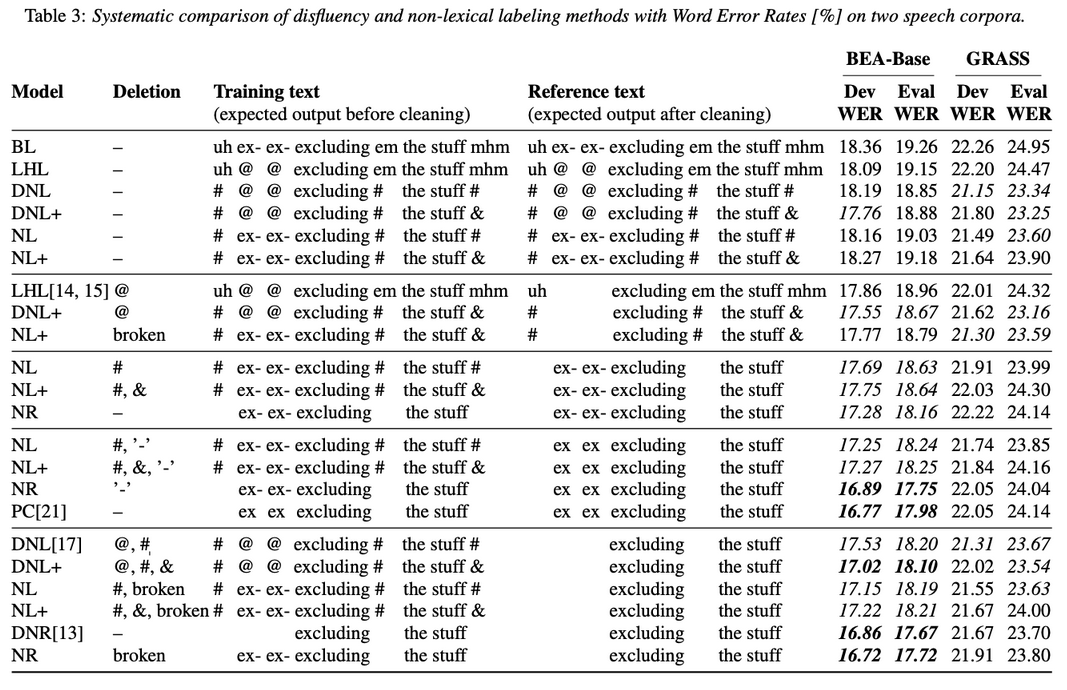
Abstract: Spontaneous speech contains a significant amount of disfluencies and non-lexical sounds (e.g., backchannels, filled pauses), which are often difficult to transcribe. Disfluency labeling for automatic speech recognition (ASR) aims at editing these phenomena in the transcription to improve overall recognition accuracy. Such labeling techniques typically delete nonlexical/disfluent labels from the prediction, where classical ASR techniques either ignore or treat them as lexical items. Our results, obtained by systematic comparison and detailed evaluation of various disfluency labeling methods on two different language conversational corpora, suggest that neither of the previous approaches are optimal. We propose to distinguish between filled pauses and meaningful conversational grunts and show that keeping the non-lexical labels is not only possible but as low as 7% label error rates can be achieved for highly important categories (including ’mhm’) while preserving a decent WER. Index Terms: end-to-end speech recognition, disfluency, conversational speech, filled pauses, Hungarian, Austrian German...
In future wireless networks, the availability of information on the position of mobile agents and the propagation environment can enable new services and increase the throughput and robustness of communications. Multipath-based simultaneous localization and mapping (SLAM) aims at estimating the position of agents and reflecting features in the environment by exploiting the relationship between the local geometry and multipath components (MPCs) in received radio signals. Existing multipath-based SLAM methods preprocess received radio signals using a channel estimator. The channel estimator lowers the data rate by extracting a set of dispersion parameters for each MPC. These parameters are then used as measurements for SLAM. Bayesian estimation for multipath-based SLAM is facilitated by the lower data rate. However, due to finite resolution capabilities limited by signal bandwidth, channel estimation is prone to errors and MPC parameters may be extracted incorrectly and lead to a reduced SLAM performance. We propose a multipath-based SLAM...
Multipath-based simultaneous localization and mapping (MP-SLAM) is a promising approach in wireless networks for obtaining position information of transmitters and receivers as well as information on the propagation environment. MP-SLAM models specular reflections of radio frequency (RF) signals at flat surfaces as virtual anchors (VAs), the mirror images of base stations (BSs). Conventional methods for MP-SLAM consider a single mobile terminal (MT) which has to be localized. The availability of additional MTs paves the way for utilizing additional information in the scenario. Specifically enabling MTs to exchange information allows for data fusion over different observations of VAs, made by different MTs, and cooperative localization. Furthermore, an inertial measurement unit (IMU) was integrated as an additional sensor for each MT unlocking additional information for orientation and state transition estimation allowing to cope with complex trajectories. Utilizing this additional information enables more robust mapping and higher localization accuracy. The paper was accepted...
This paper investigates the prosody of sentences elicited in three Information Structure (IS) conditions: all-new, theme-rheme and rhematic focus-background. The sentences were produced by 18 speakers of Egyptian Arabic (EA). This is the first quantitative study to provide a comprehensive analysis of holistic f0 contours (by means of GAMM) and configurations of f0, duration and intensity (by means of FPCA) associated with the three IS conditions, both across and within speakers. A significant difference between focus-background and the other information structure conditions was found, but also strong inter-speaker variation in terms of strategies and the degree to which these strategies were applied. The results suggest that post-focus register lowering and the duration of the stressed syllables of the focused and the utterance-final word are more consistent cues to focus than a higher peak of the focus accent. In addition, some independence of duration and intensity from f0 could be identified....

I’m happy to announce the publication of a special issue of the Journal of Advances in Information Fusion (JAIF), which I have guest edited together with my collaborator Florian Meyer of UCSD! It contains the paper “Multipath-Based SLAM for Non-Ideal Reflective Surfaces Exploiting Multiple-Measurements” written by members of our research team: Lukas Wielandner, Alexander Venus, Thomas Wilding, and myself. If you are interested have a look here.
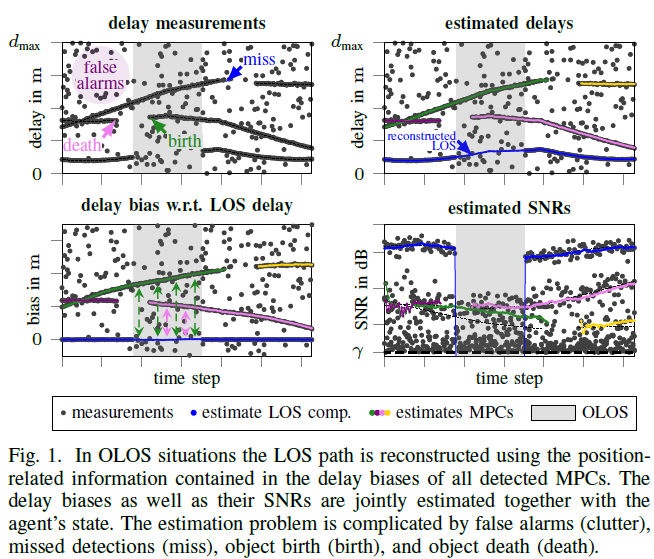
We present a factor graph formulation and particlebased sum-product algorithm for robust localization and tracking in multipath-prone environments. The proposed sequential algorithm jointly estimates the mobile agent’s position together with a time-varying number of multipath components (MPCs). The MPCs are represented by “delay biases” corresponding to the offset between line-of-sight (LOS) component delay and the respective delays of all detectable MPCs. The delay biases of the MPCs capture the geometric features of the propagation environment with respect to the mobile agent. Therefore, they can provide position-related information contained in the MPCs without explicitly building a map of the environment. We demonstrate that the position-related information enables the algorithm to provide high-accuracy position estimates even in fully obstructed line-of-sight (OLOS) situations. Using simulated and real measurements in different scenarios we demonstrate the proposed algorithm to significantly outperform state-of-the-art multipath-aided tracking algorithms and show that the performance of our algorithm constantly attains...
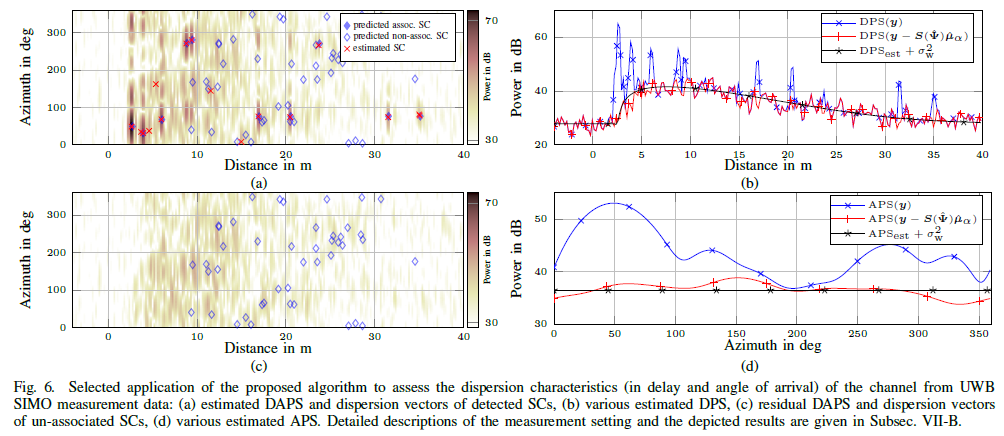
In this paper, we present an iterative algorithm that detects and estimates the specular components (SCs) and estimates the dense component (DC) of single-input—multipleoutput (SIMO) ultra-wide-band (UWB) multipath channels. Specifically, the algorithm super-resolves the SCs in the delay–angle-of-arrival domain and estimates the parameters of a parametric model of the delay-angle power spectrum characterizing the DC. Channel noise is also estimated. In essence, the algorithm solves the problem of estimating spectral lines (the SCs) in colored noise (generated by the DC and channel noise). Its design is inspired by the sparse Bayesian learning (SBL) framework. As a result the iteration process contains a threshold condition that determines whether a candidate SC shall be retained or pruned. By relying to results from extreme-value analysis the threshold of this condition is suitably adapted to ensure a prescribed probability of detecting spurious SCs. Studies using synthetic and real channel measurement data demonstrate the virtues...
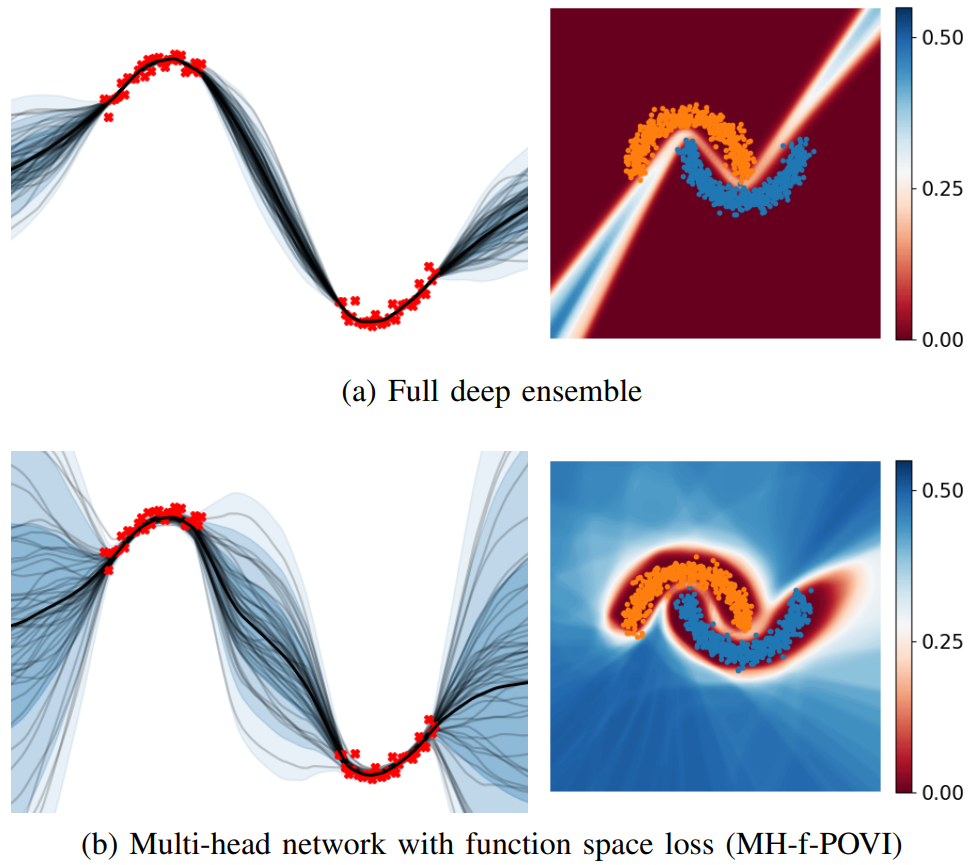
Deep ensembles have shown remarkable empirical success in quantifying uncertainty, albeit at considerable computational cost and memory footprint. Meanwhile, deterministic single-network uncertainty methods have proven as computationally effective alternatives, providing uncertainty estimates based on distributions of latent representations. While those methods are successful at out-of-domain detection, they exhibit poor calibration under distribution shifts. In this work, we propose a method that provides calibrated uncertainty by utilizing particle-based variational inference in function space. Rather than using full deep ensembles to represent particles in function space, we propose a single multi-headed neural network that is regularized to preserve bi-Lipschitz conditions. Sharing a joint latent representation enables a reduction in computational requirements, while prediction diversity is maintained by the multiple heads. We achieve competitive results in disentangling aleatoric and epistemic uncertainty for active learning, detecting out-of-domain data, and providing calibrated uncertainty estimates under distribution shifts while significantly reducing compute and memory requirements.
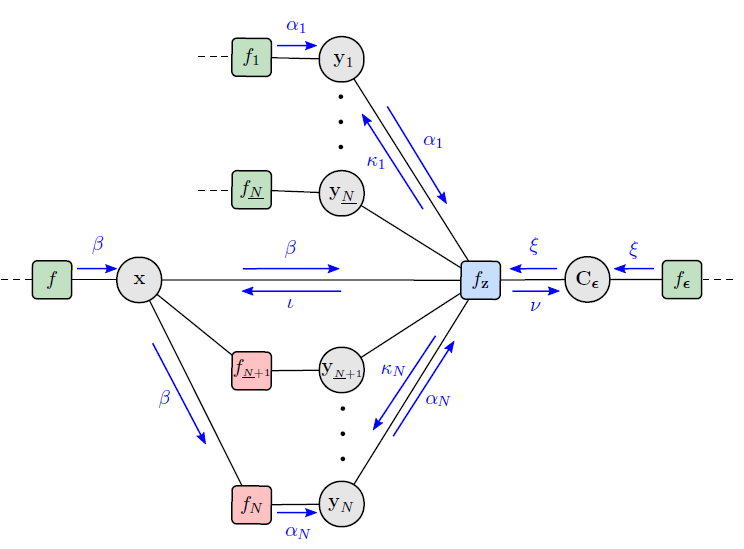
In this work, we develop a multipath-based simultaneous localization and mapping (SLAM) method that can directly be applied to received radio signals. In existing multipath-based SLAM approaches, a channel estimator is used as a preprocessing stage that reduces data flow and computational complexity by extracting features related to multipath components (MPCs). We aim to avoid any preprocessing stage that may lead to a loss of relevant information. The presented method relies on a new statistical model for the data generation process of the received radio signal that can be represented by a factor graph. This factor graph is the starting point for the development of an efficient belief propagation (BP) method for multipath-based SLAM that directly uses received radio signals as measurements. Simulation results in a realistic scenario with a single-input single-output (SISO) channel demonstrate that the proposed direct method for radio-based SLAM outperforms state-of-the-art methods that rely on a...
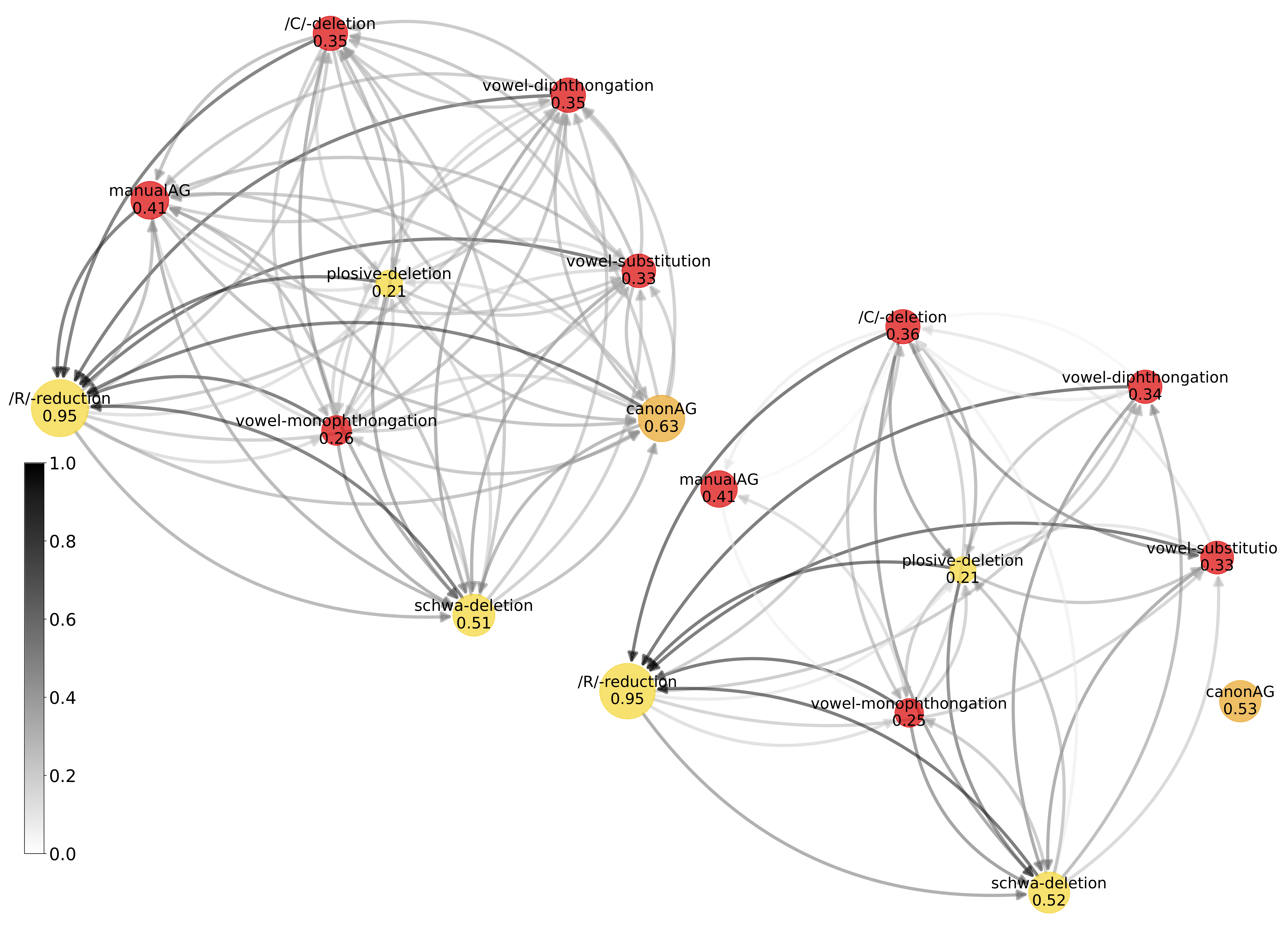
Given the development of automatic speech recognition based techniques for creating phonetic annotations of large speech corpora, there has been a growing interest in investigating the frequencies of occurrence of phonological and reduction processes. Given that most studies have analyzed these processes separately, they did not provide insights about their co-occurrences. This paper contributes with introducing graph theory methods for the analysis of pronunciation variation in GRASS, a large corpus of Austrian German conversational speech. More specifically, we investigate how reduction processes that are typical for spontaneous German in general (figure: yellow) co-occur with phonological processes typical for the Austrian German variety (figure: red). Whereas our concrete findings are of special interest to scientists investigating variation in German, the approach presented opens new possibilities to analyze pronunciation variation in large corpora of across speakers and across speaking styles in any language. This work has been presented at Interspeech 2023, Dublin....
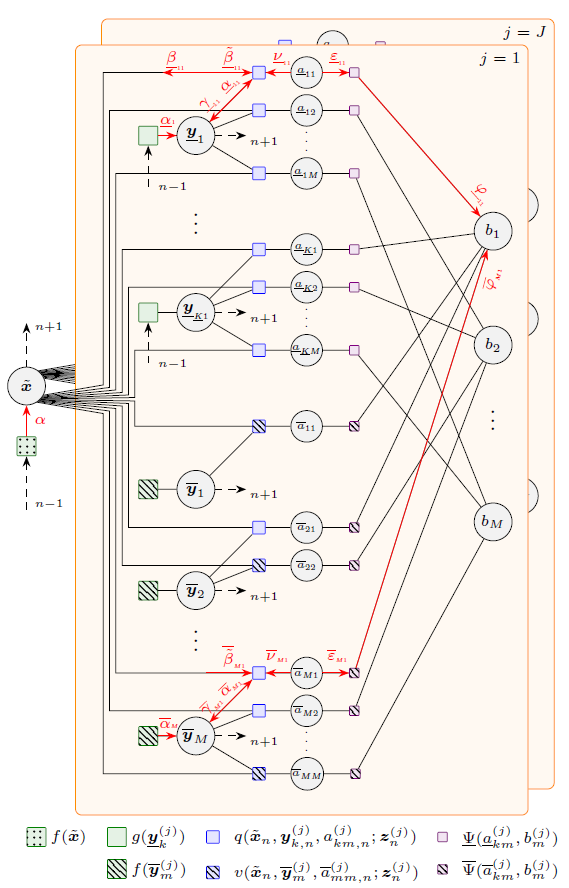
Multipath-based simultaneous localization and mapping (SLAM) is a promising approach to obtain position information of transmitters and receivers as well as information regarding the propagation environments in future mobile communication systems. Usually, specular reflections of the radio signals occurring at flat surfaces are modeled by virtual anchors (VAs) that are mirror images of the physical anchors (PAs). In existing methods for multipath-based SLAM, each VA is assumed to generate only a single measurement. However, due to imperfections of the measurement equipment such as non-calibrated antennas or model mismatch due to roughness of the reflective surfaces, there are potentially multiple multipath components (MPCs) that are associated to one single VA. In this paper, we introduce a Bayesian particle-based sum-product algorithm (SPA) for multipath-based SLAM that can cope with multiplemeasurements being associated to a single VA. Furthermore, we introduce a novel statistical measurement model that is strongly related to the radio signal....
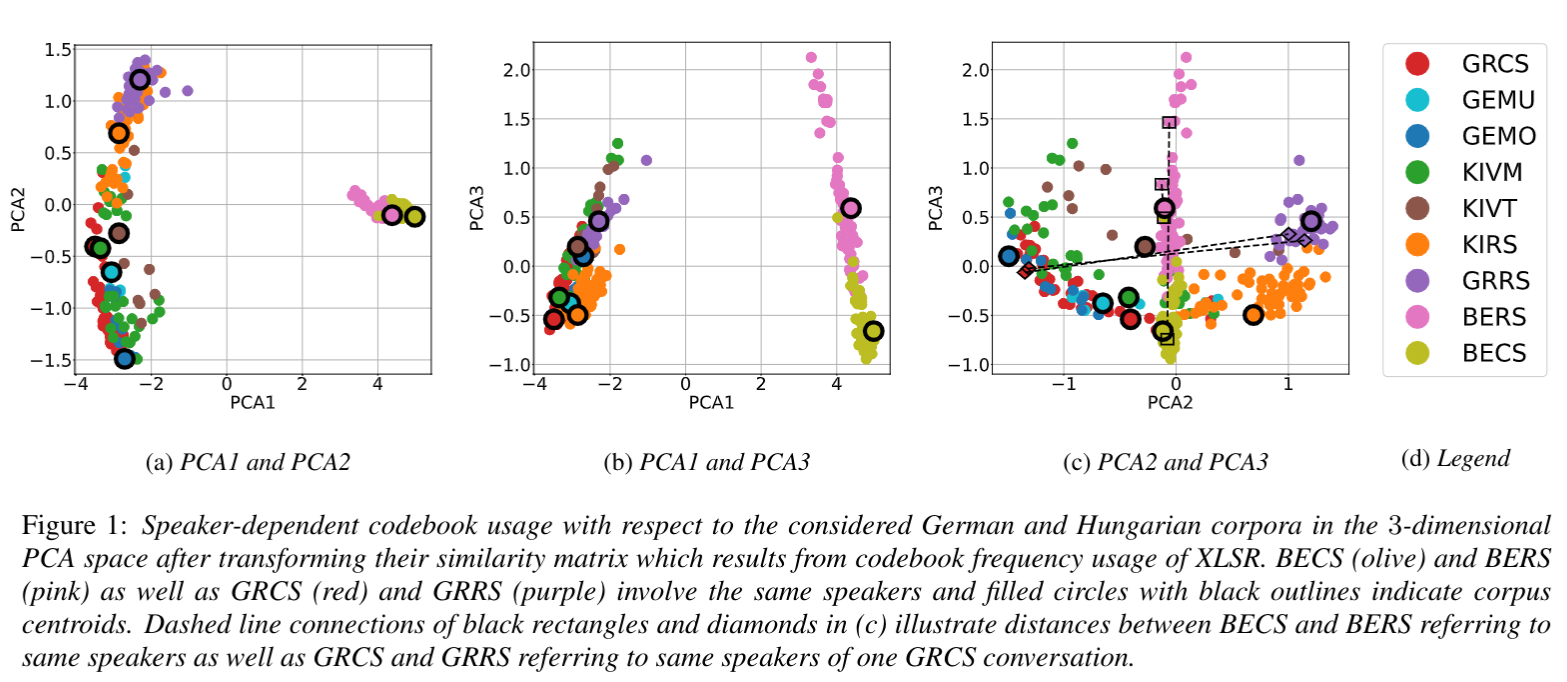
Automatic speech recognition systems based on self-supervised learning yield excellent performance for read, but not so for conversational speech. This work contributes insights into how corpora from different languages and speaking styles are encoded in shared discrete speech representations (based on wav2vec2 XLSR). We analyze codebook entries of data from two languages from different language families (i.e., German and Hungarian), of data from different varieties from the same language (i.e., German and Austrian German) and of data from different speaking styles (read and conversational speech). We find that – as expected – the two languages are clearly separable. With respect to speaking style, conversational Austrian German has the highest similarity with a corpus of similar spontaneity from a different German variety, and speakers differ more among themselves when using different speaking styles than from other speakers of a different region when using the same speaking style. This work is published...
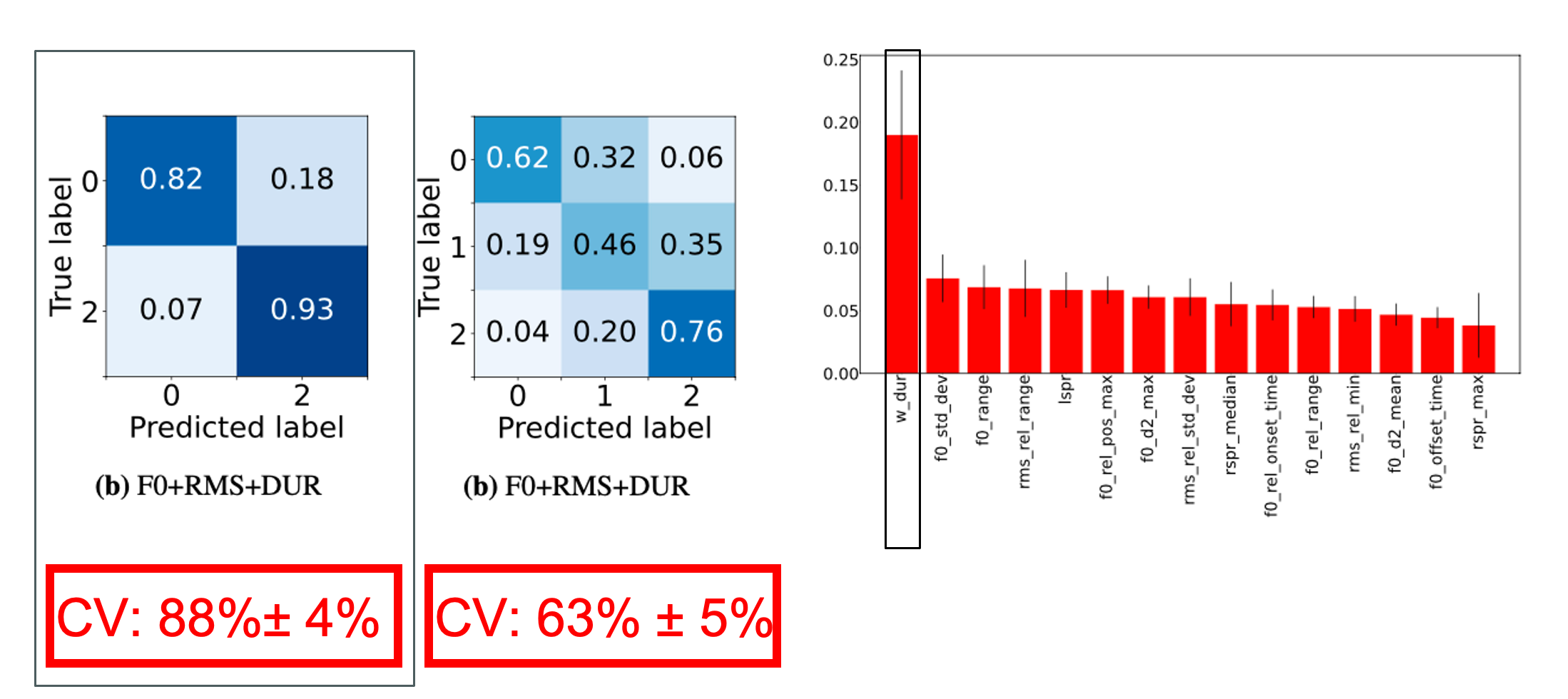
Left: Confusion matrices from experiments with 15 best features (F0+RMS+DUR). Right: Random Forest feature importances for 3 class problem with F0, RMS and DUR. This work focuses on the automatic detection of prominent words in conversational speech. Most tools for prominence detection rely on prosodic features extracted at a syllable- or phone level and their accuracy thus strongly depends on the quality of the given phone-level segmentation. Given the high degree of pronunciation variation in conversational speech, automatic phonetic segmentation is not accurate enough to detect prominence reliably. Here we explore different approaches to prominence detection that require merely a prior word-level segmentation. The first experiment shows that by using word-level prosodic features cross-validation accuracies of 88%+-4% can be reached, and that word duration is the most important feature. The second experiment introduces entropy-based fundamental frequency and intensity features for prominence detection. Our findings suggest that entropy-based, word-level features can...
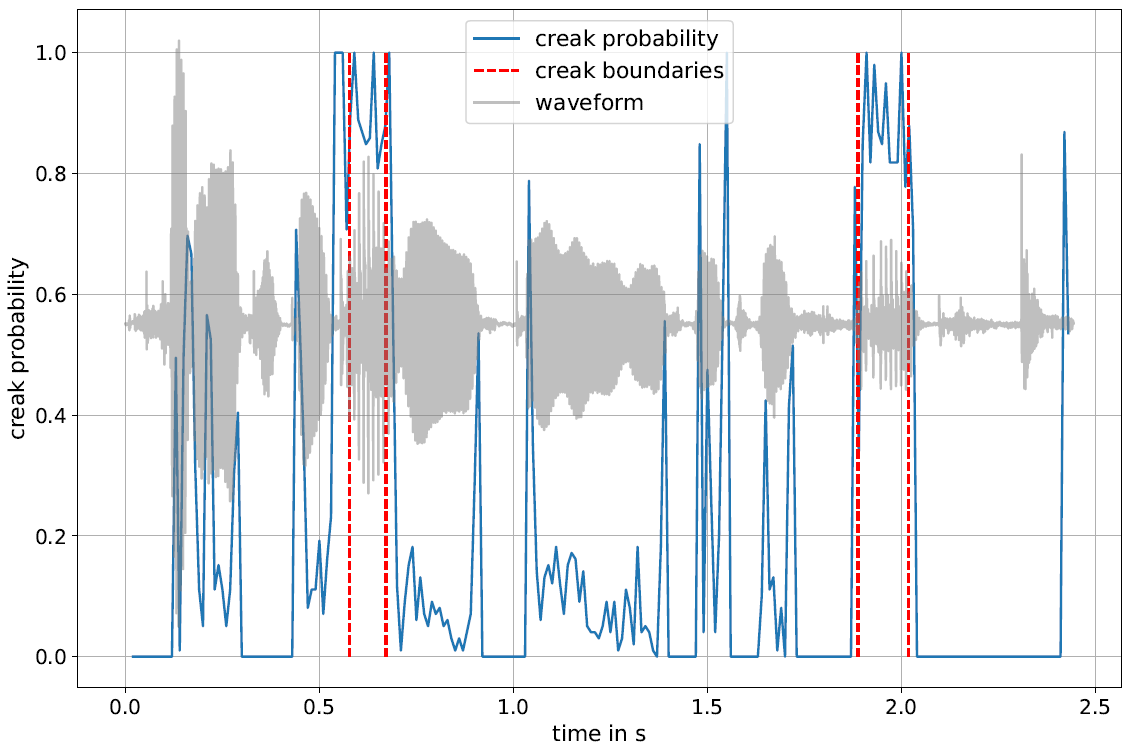
The annotation of creaky voice is relevant for various linguistic topics, from phonological analyses to the investigation of turn-taking, but manual annotation is a time-consuming process. In this paper, we present creapy, a Python-based tool to detect creaky intervals in speech signals. creapy does not require prior phonetic segmentation and supports the export of Praat TextGrid files, allowing for manual revision of the automatically labelled intervals. creapy was developed and tested using Austrian German conversational speech. It was optimised for recall to facilitate a semi-automatic annotation process, and it achieved a better performance for men’s (recall: .79) than for women’s voices (recall: .60). This work by Michael Paierl and Thomas Röck is accepted for presentation at the 20th International Congress of Phonetic Sciences – ICPhS 2023. To use creapy, checkout this repository.
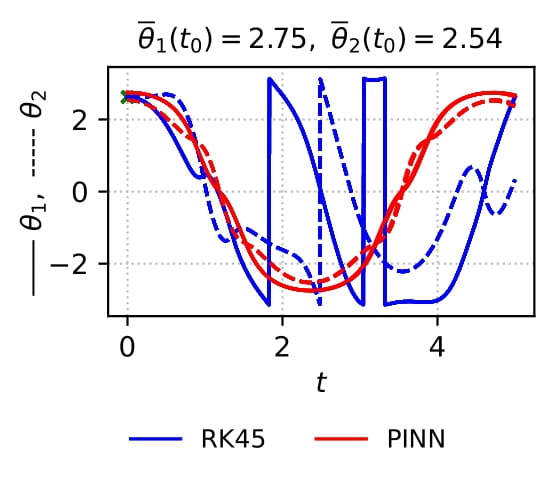
Physics-informed neural networks are a deep learning approach to solving differential equations given only information about the initial and boundary conditions. PINNs are easy to implement and have many desirable properties, such as being mesh-free. Unfortunately, it has been shown that training PINNs is not so straightforward - convergence problems often arise when simulating dynamical systems with high-frequency components, chaotic or turbulent behavior. In this work, we have focused on understanding the underlying reasons for the difficulties in training PINNs by performing experiments on the double pendulum. Our results show that PINNs are not sensitive to perturbations in the initial condition. Instead, the PINN optimization consistently converges to physically correct solutions that only marginally violate the initial condition, but diverge significantly from the desired solution due to the chaotic nature of the system. We hypothesize that the PINNs “cheat” by shifting the initial conditions to values that correspond to physically...
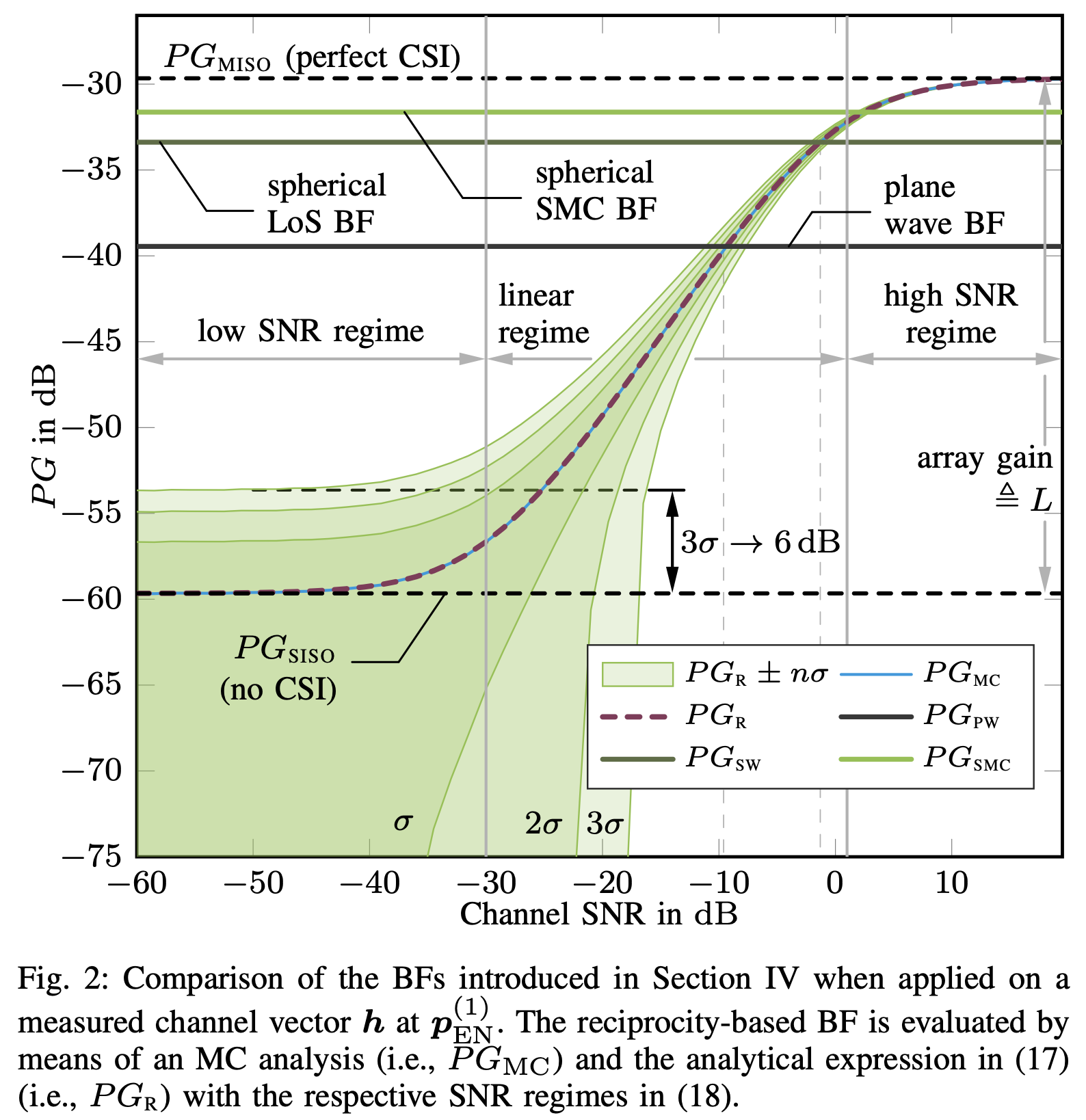
Massive antenna arrays form physically large apertures with a beam-focusing capability, leading to outstanding wireless power transfer (WPT) efficiency paired with low radiation levels outside the focusing region. However, leveraging these features requires accurate knowledge of the multipath propagation channel and overcoming the (Rayleigh) fading channel present in typical application scenarios. For that, reciprocity-based beamforming is an optimal solution that estimates the actual channel gains from pilot transmissions on the uplink. But this solution is unsuitable for passive backscatter nodes that are not capable of sending any pilots in the initial access phase. Using measured channel data from an extremely large-scale MIMO (XL-MIMO) testbed, we compare geometry-based planar wavefront and spherical wavefront beamformers with a reciprocity-based beamformer, to address this initial access problem. We also show that we can predict specular multipath components (SMCs) based only on geometric environment information. We demonstrate that a transmit power of 1W is sufficient...
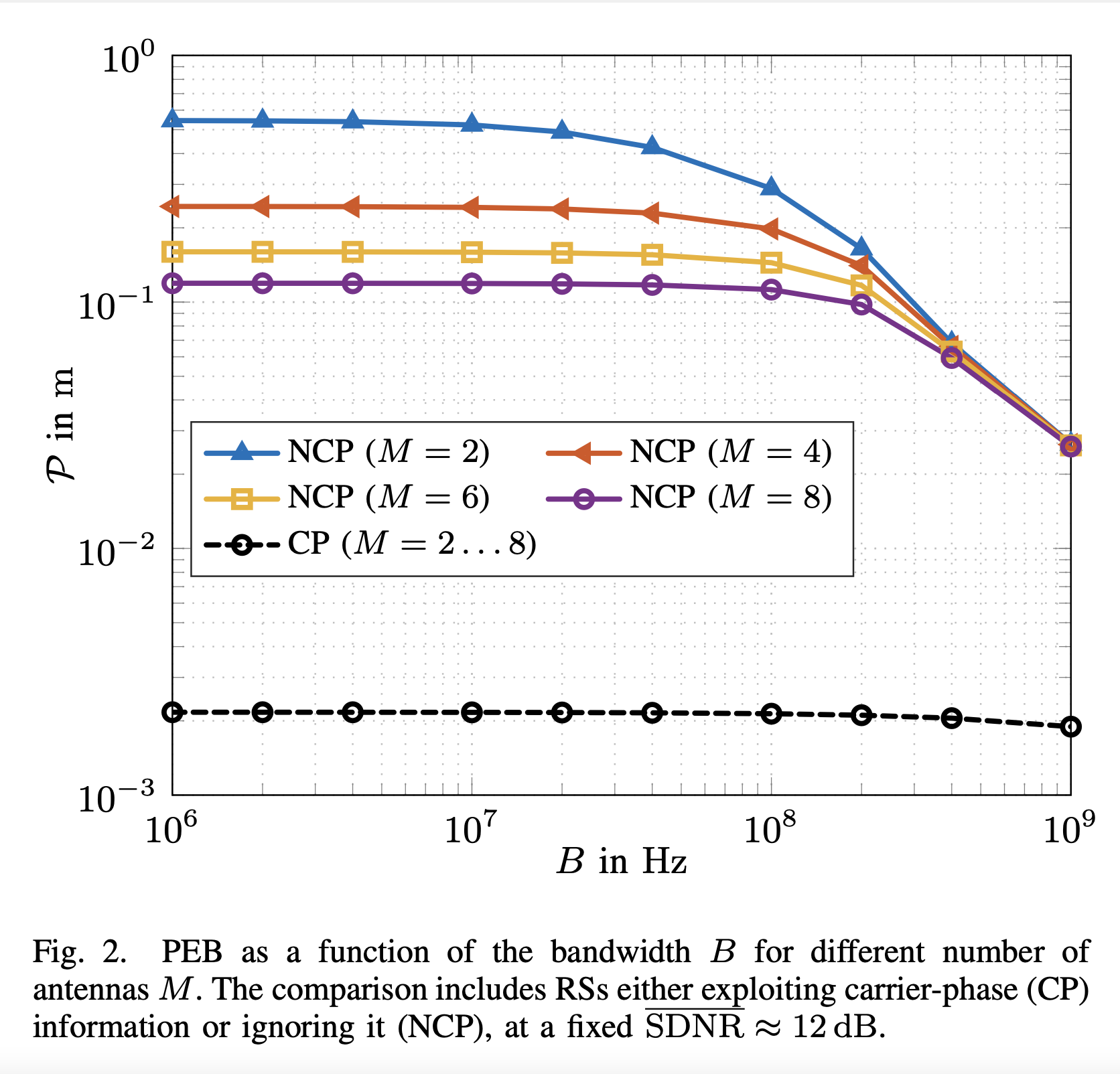
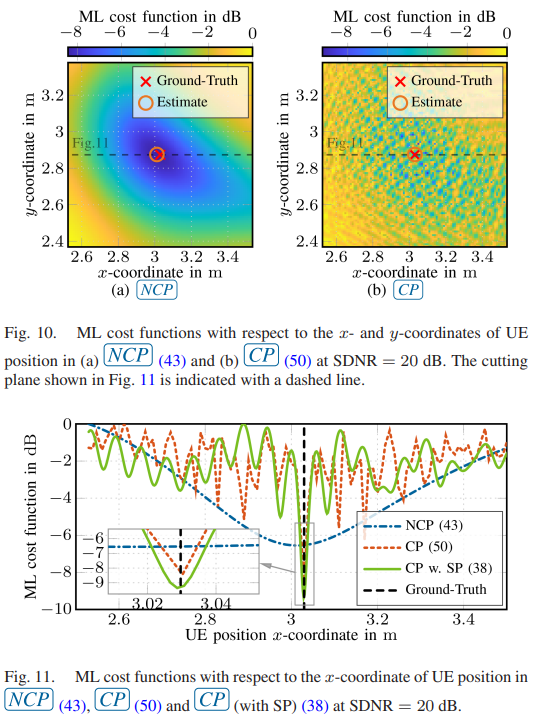
Radio stripes (RSs) is an emerging technology in beyond 5G and 6G wireless networks to support the deployment of cell-free architectures. This joint work investigates the potential use of RSs to enable joint positioning and synchronization in the uplink channel at sub-6 GHz bands. The considered scenario consists of a single-antenna user equipment (UE) that communicates with a network of multiple-antenna RSs distributed over a wide area. The UE is assumed to be unsynchronized to the RSs network, while individual RSs are time- and phase-synchronized. We formulate the problem of joint estimation of position, clock offset, and phase offset of the UE and derive the corresponding maximum-likelihood (ML) estimator, both with and without exploiting carrier phase information. Our team at the SPSC Lab contributed a Fisher information analysis to gain fundamental insights into the achievable performance and to inspect the theoretical lower bounds numerically. Simulation results demonstrate that a promising...
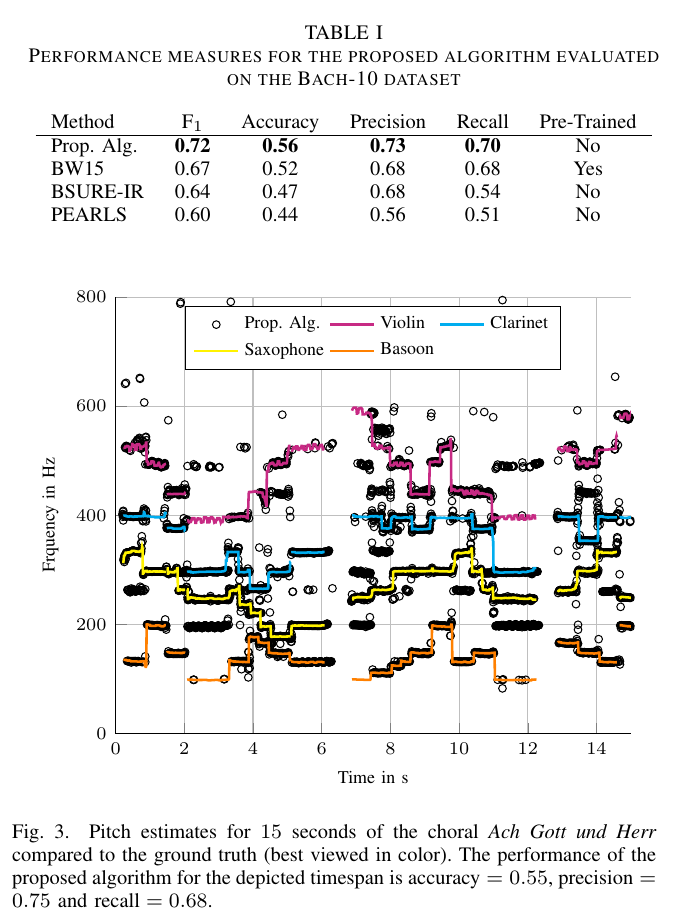
We developed a variational Bayesian inference algorithm for structured line spectra that actively exploits the structure that naturally occurs in many applications to improve estimation performance. For example, consider the audio signal produced by several notes played together in a chord. Each note is a line spectrum with a harmonic structure, i.e. each line is at a multiple of some fundamental frequency - the pitch of the note. When several notes are played together, the result is a linespectrum that is a mixture of several harmonic spectra. By explicitly considering the structure in each harmonic spectrum, our proposed method is able to outperform state-of-the-art multi-pitch estimation methods on the Bach-10 dataset, even machine learning methods pre-trained on the instruments in the dataset. An example of the detected pitch for several seconds of the chorale “Ach Gott und Herr” from the dataset is shown in the figure. Structured line spectra occur...
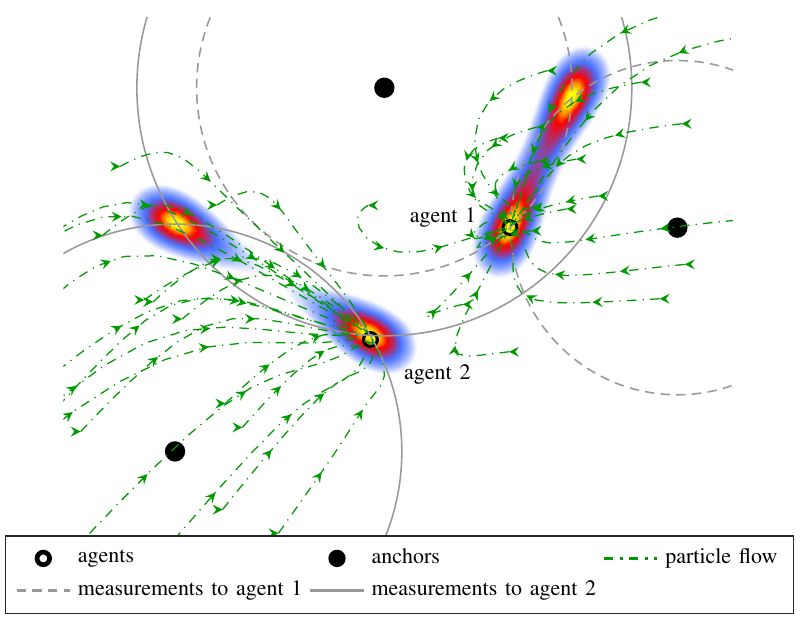
This paper derives the messages of belief propagation (BP) for cooperative localization by means of particle flow, leading to the development of a distributed particle-based message-passing algorithm which avoids particle degeneracy. Our combined particle flow-based BP approach allows the calculation of highly accurate proposal distributions for agent states with a minimal number of particles. It outperforms conventional particle-based BP algorithms in terms of accuracy and runtime. Furthermore, we compare the proposed method to a centralized particle flow-based implementation, known as the exact Daum-Huang filter, and to sigma point BP in terms of position accuracy, runtime, and memory requirement versus the network size. We further contrast all methods to the theoretical performance limit provided by the posterior Cramer-Rao lower bound. Based on three different scenarios, we demonstrate the superiority of the proposed method. Figure: Visualization of the particle flow (dash-dotted green lines) of two cooperating agents in the vicinity of three...
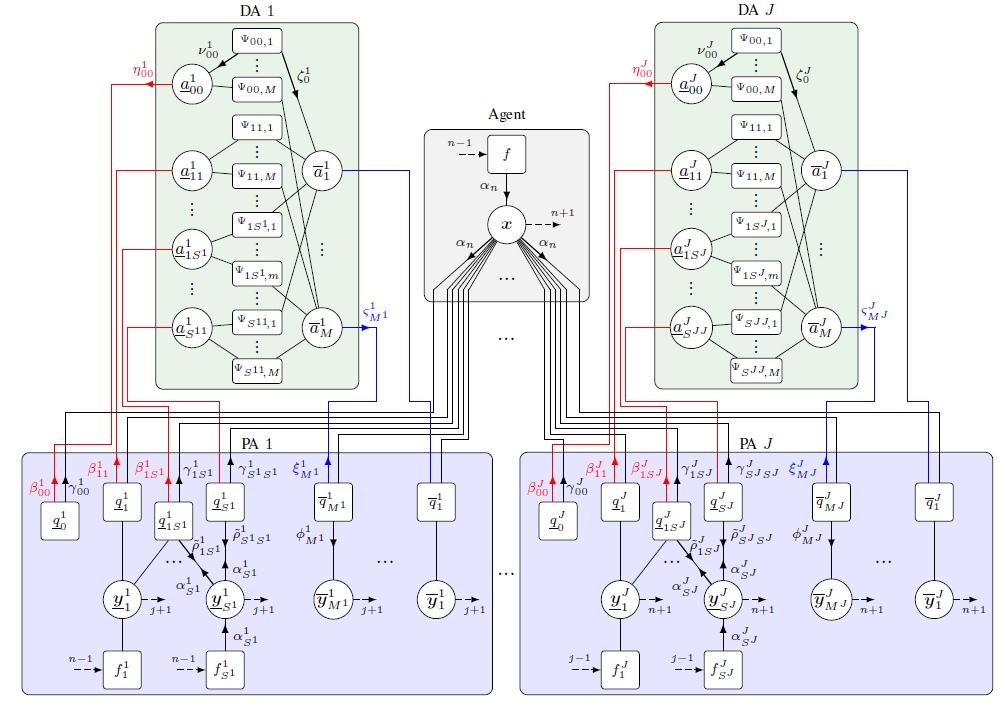
Multipath-based simultaneous localization and mapping (SLAM) is an emerging paradigm for accurate indoor localization with limited resources. The goal of multipath-based SLAM is to detect and localize radio reflective surfaces to support the estimation of time-varying positions of mobile agents. Radio reflective surfaces are typically represented by so-called virtual anchors (VAs), which are mirror images of base stations at the surfaces. In existing multipath-based SLAM methods, a VA is introduced for each propagation path, even if the goal is to map the reflective surfaces. The fact that not every reflective surface but every propagation path is modeled by a VA, complicates a consistent combination “fusion” of statistical information across multiple paths and base stations and thus limits the accuracy and mapping speed of existing multipath-based SLAM methods. In this paper, we introduce an improved statistical model and estimation method that enables data fusion for multipath-based SLAM by representing each surface...
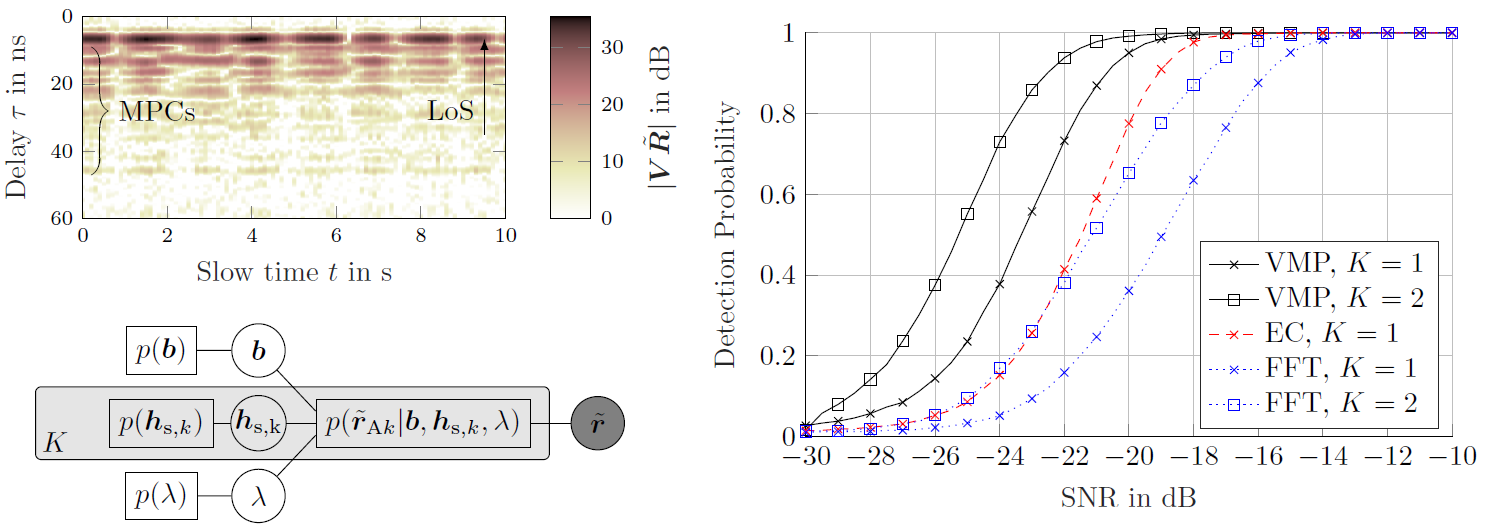
We apply an variational message passing scheme in order to detect the presence of children im parked cars using multistatic UWB radar. To detect a person in a car, we use a structured mean field approach an apply variational message passing to maximize the ELBO, a lower bound on the model evidence. The ELBO is then used to calculate the odds-ratio of the two cases (the car being either empty or occupied). During the inference process, the radar channel and the respiratory chest motion of the target ar estimated, in order to coherently add up all of the energy from the target present in the received signal. Therefore, we make not only use of the direct interaction of the target with the transmitted signal (line-of-sight, LoS), but also of the multipath components (MPCs) that bounce around in the car before interacting with the target, which increases the SNR. Since the...
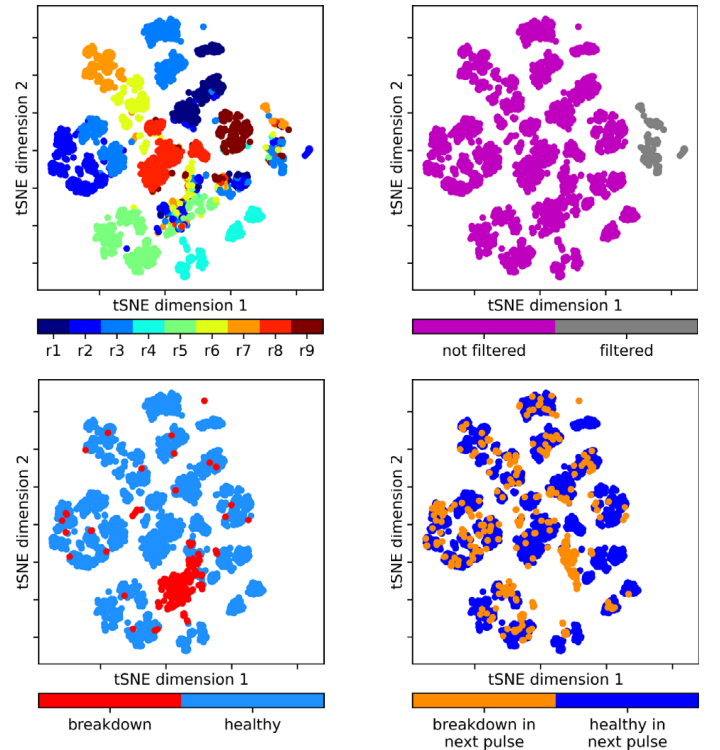
In our latest project with CERN, we used machine learning to analyze breakdowns in a test bench for the CLIC accelerator. In particle accelerators, one of the most prevalent limits on high-gradient operation is the occurrence of vacuum arcs, commonly known as radio frequency (RF) breakdowns. During a breakdown, field enhancement, associated with small deformations on the cavity surface, results in electrical arcs which may irreparably damage the RF cavity surface. In the project, supervised and unsupervised methods were used for data analysis and a breakdown prediction study. ‘Explainable-AI’ made it possible to interpret learned model parameters and to reverse engineer physical properties in the test bench. Similar models could be applied to cancer treatment, light sources, and CERN next generation high energy physics facilities. The work was recently published in the Journal of Physical Review Accelerators and Beams (PRAB) and is available here.

Belief propagation (BP) is a popular method for performing probabilistic inference on graphical models. In this work we show how one can improve the performance of BP by solving a sequence of models that starts with independent variables. We term this approach self-guided belief propagation (SBP) and theoretically demonstrate that SBP finds the global optimum of the Bethe approximation for attractive models where all variables favor the same state .Moreover, we apply SBP to various graphs (random ones, and graphs corresponding to problems in wireless communications and computer vision) and show that (i) SBP is superior in terms of accuracy whenever BP converges, and (ii) SBP obtains a unique, stable, and accurate solution whenever BP does not converge. More information can be found in our [paper][https://ieeexplore.ieee.org/abstract/document/9852264] Figure: Image corrupted with salt and pepper noise. BP reduces the noise but struggles with reconstructing the boundary regions; SBP reduces the noise as...
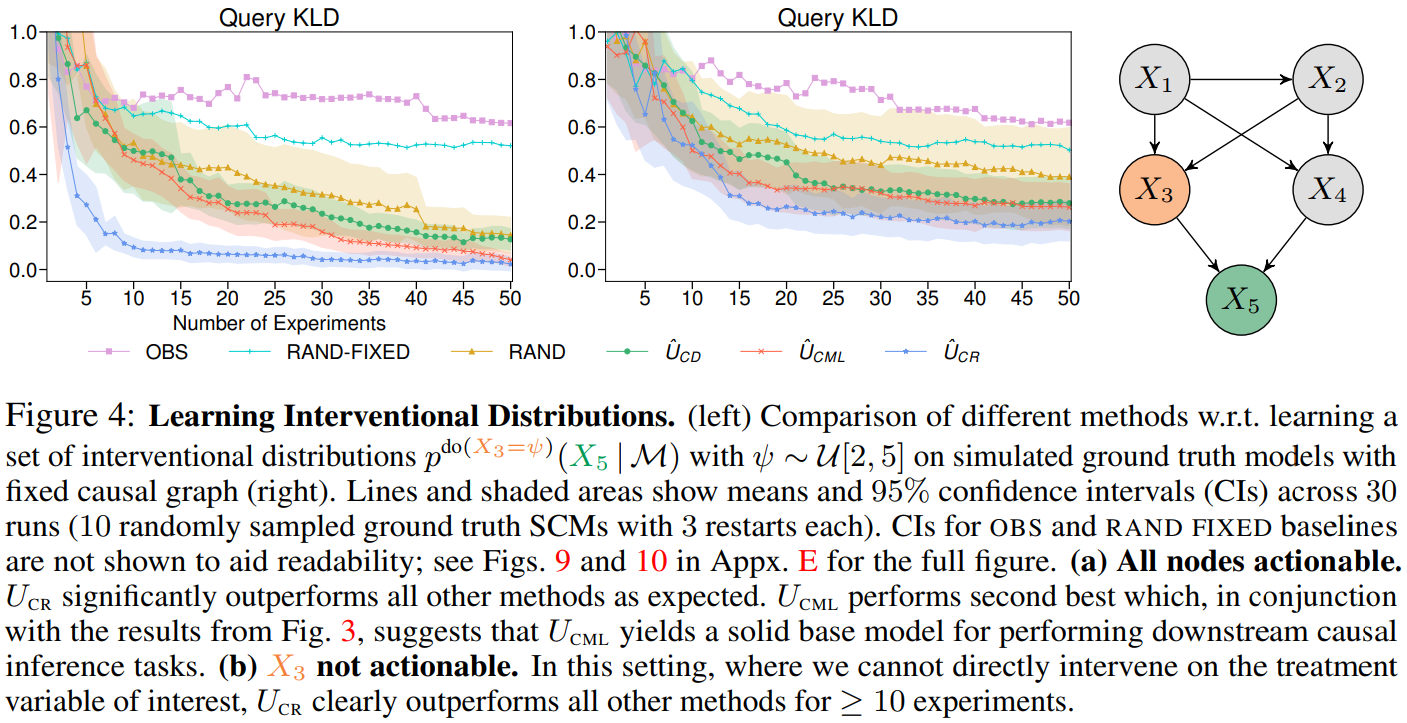
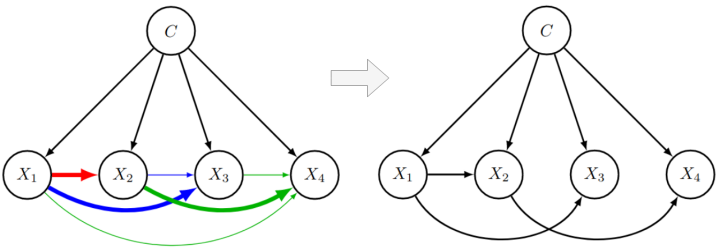
Causal discovery and causal reasoning are classically treated as separate and consecutive tasks: one first infers the causal graph, and then uses it to estimate causal effects of interventions. However, such a two-stage approach is uneconomical, especially in terms of actively collected interventional data, since the causal query of interest may not require a fully-specified causal model. From a Bayesian perspective, it is also unnatural, since a causal query (e.g., the causal graph or some causal effect) can be viewed as a latent quantity subject to posterior inference—other unobserved quantities that are not of direct interest (e.g., the full causal model) ought to be marginalized out in this process and contribute to our epistemic uncertainty. In this work, we propose Active Bayesian Causal Inference (ABCI), a fully-Bayesian active learning framework for integrated causal discovery and reasoning, which jointly infers a posterior over causal models and queries of interest. In our...
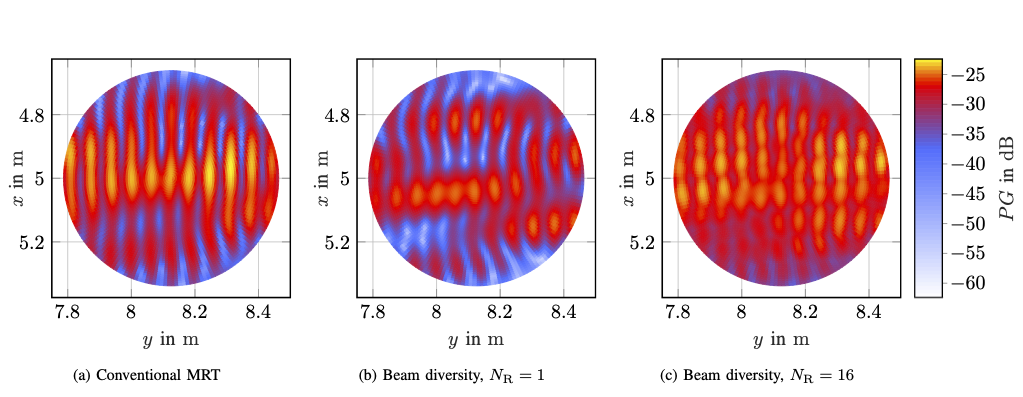
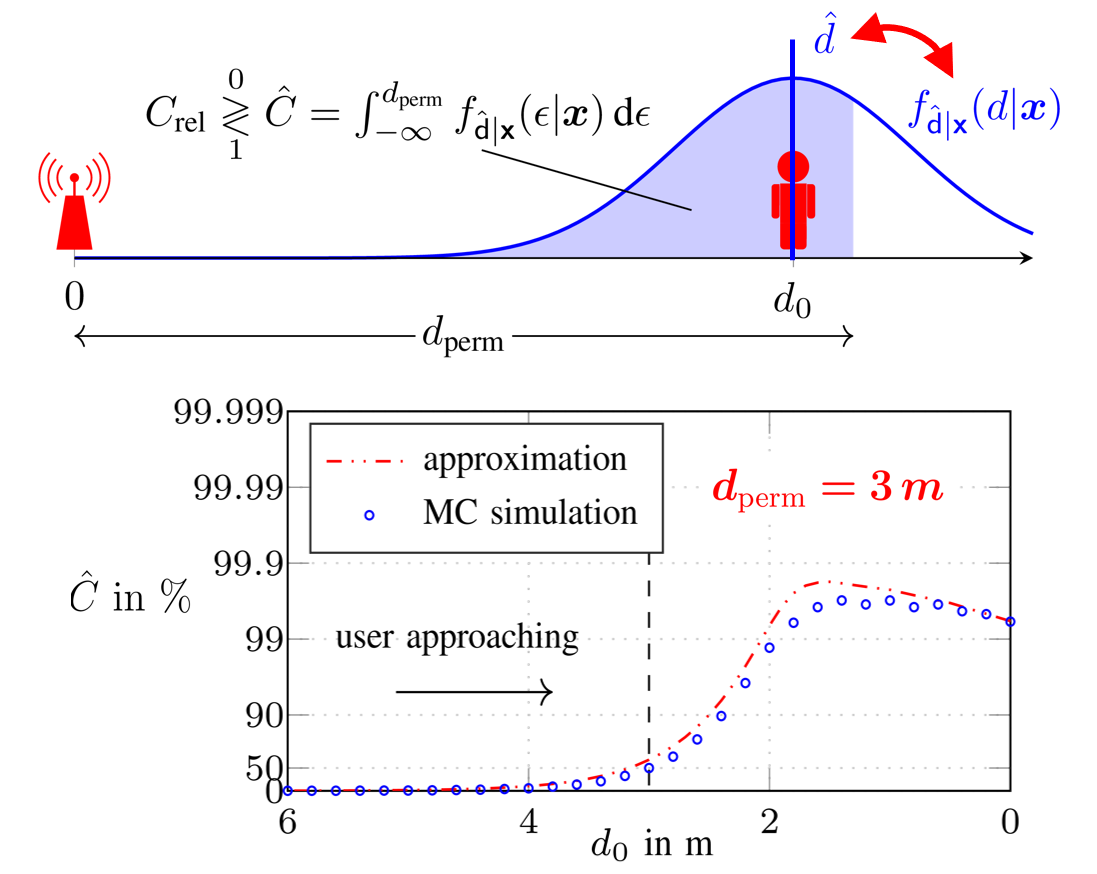
Within the REINDEER H2020 project, we investigate the potential of using physically large, or distributed antenna arrays to transmit power wirelessly to batteryless energy neutral (EN) devices. An enabling milestone to make the technology feasible is solving the initial-access problem, i.e., waking up an EN device with unknown channel state information (CSI). One possible approach for initial access is beam sweeping, where the transmit array sweeps beams sequentially according to a predefined codebook to power up an EN device for the first time. However, beam sweeping in indoor scenarios suffers from fading due to severe multipath propagation, possibly originating from unknown objects in the environment. In our paper, we exploit environment-awareness to predict CSI. We establish a simultaneous multibeam transmission which intentionally leverages specular reflections to illuminate an EN device and improve its power budget over what is achievable using a single line-of-sight beam only. We vary the phases of...
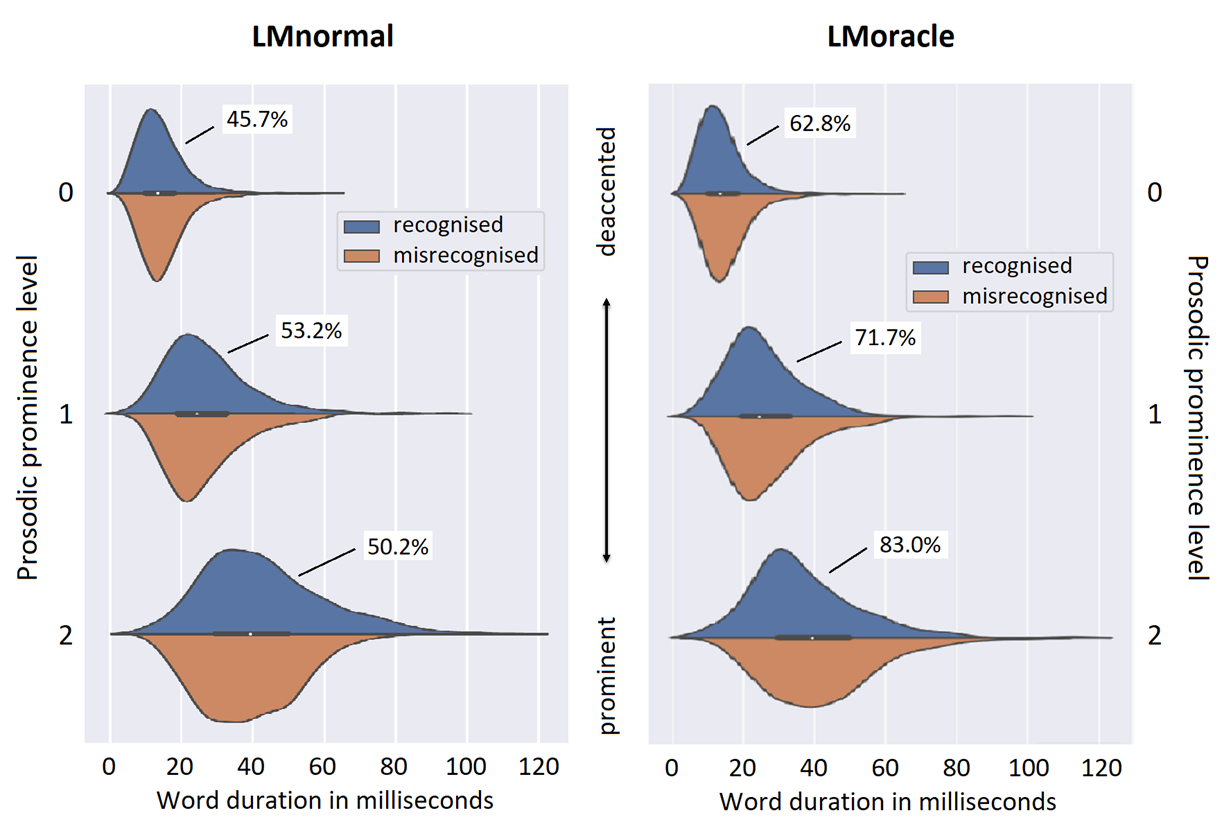
The performance of Automatic Speech Recognition (ASR) systems varies with the speaking style of the data that is to be recognised. Where read speech, voice commands and also broadcast news are nowadays well recognised by standard ASR systems, conversational speech remains to be challenging for multiple reasons. We compared recognition performance of two Language Models (LMs): 1) an ordinary 4-gram “LMnormal” and 2) an oracle 4-gram “LMoracle” that was trained on all the utterances of a corpus of conversational speech (GRASS), including data of the evaluation set. We analysed specific (mis-)recognised word tokens for their prosodic characteristics. In general, high-frequent words are easy to recognise since they are well-known to both the acoustic models and the language model in various contexts. For both LMs, we found that short, high-frequent words are misrecognised more often than longer words that have lower frequency of occurence in our data. Short, high-frequent tokens are...
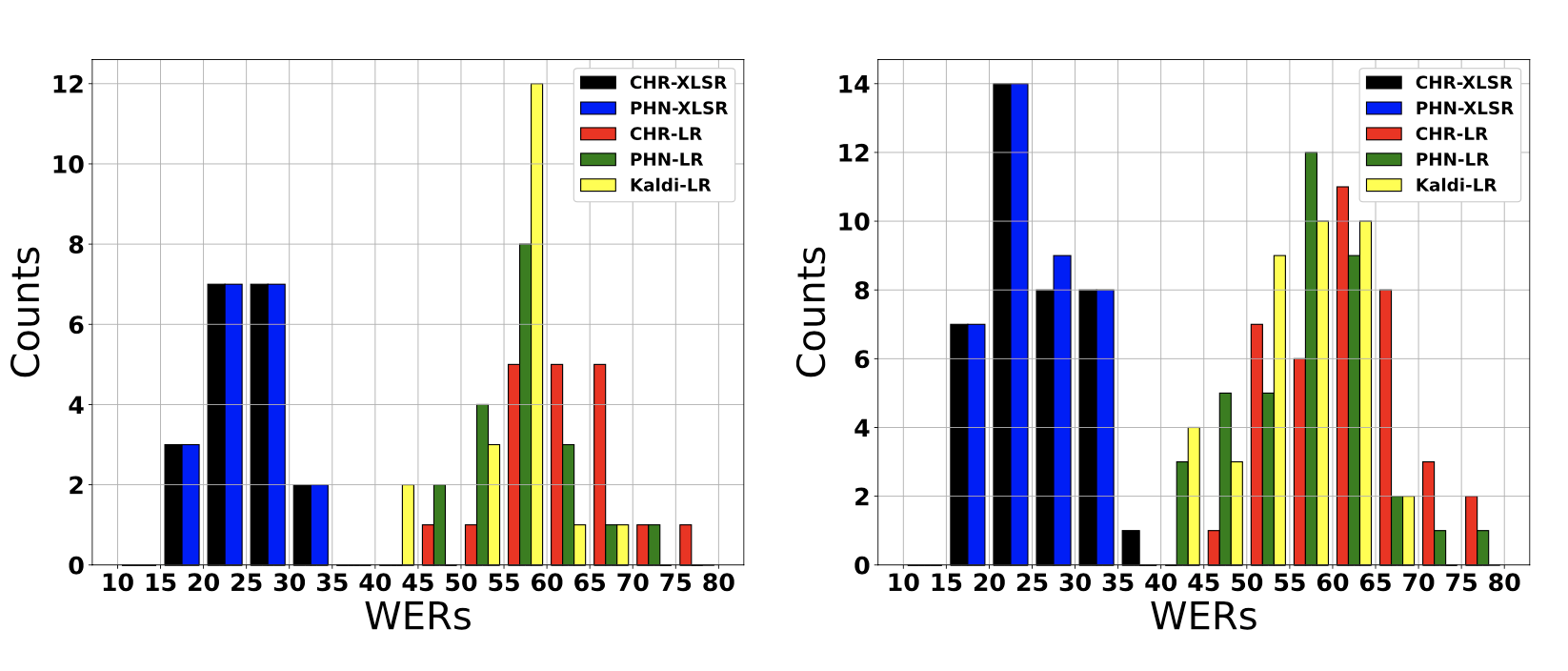
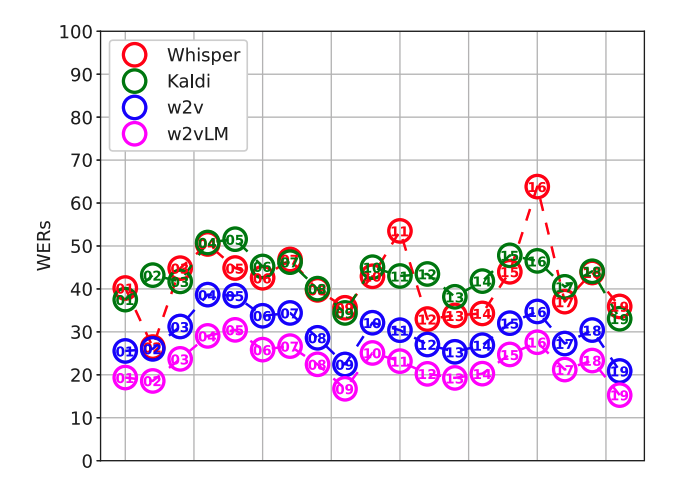
Left: Histogram showing conversation-dependent WERs of low-resource (LR) and data-driven (XLSR) 4-gram models. Right: Histogram showing speaker-dependent WERs of low-resource (LR) and data-driven (XLSR) 4-gram models. We show that data-driven speech recognition systems are effective for Austrian German conversational speech but we still observe a lack of robustness to inter-speaker and inter-conversation variation. Low-resource (LR) speech recognition is challenging since two humans who interact spontaneously with each other introduce complex inter- and intra-speaker variation depending on for instance the speaker’s attitude towards the listener and the speaking task. Recent developments in self-supervision have allowed LR-scenarios to take advantage of large amounts of otherwise unrelated data. In this study, we characterize an (LR) Austrian German conversational task. We begin with a non-pre-trained baseline (Kaldi-LR) and show that fine-tuning of a model pre-trained using self-supervision (XLSR) leads to improvements consistent with those in the literature; this extends to cases where a lexicon...
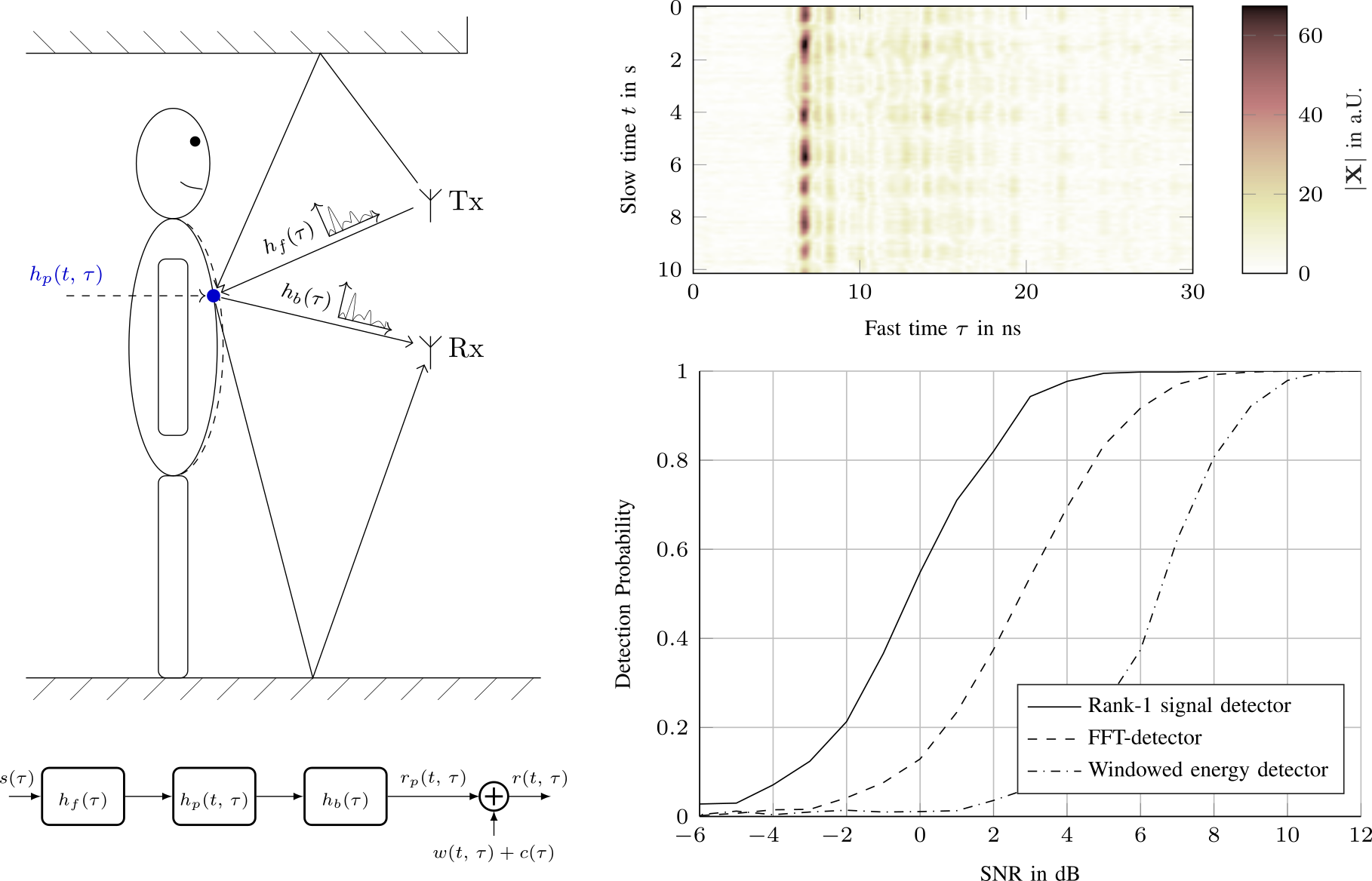
We show, that the UWB nodes of the keyless-access system of a car can be used as radar sensors to detect if the car is occupied. To distinguish the occupant from the static clutter background, we detect the breathing motion of the occupant’s chest. The influence of the chest motion on the received signal is modelled as a backscatter channel. Evaluating this model revealed, that the received signal is the outer product of the breathing motion and channel delay profile. Modelling the breathing motion and channel as gaussian processes with known covariance, the optimal decision criterion is given by the estimator-correlator. Monte-Carlo performance analysis showed a 3dB increase in the detection threshold compared to a FFT-based detector and, thus, confirms our results. This work was presented at the 2021 European Radar Conference and will be published in the accompanying proceedings.
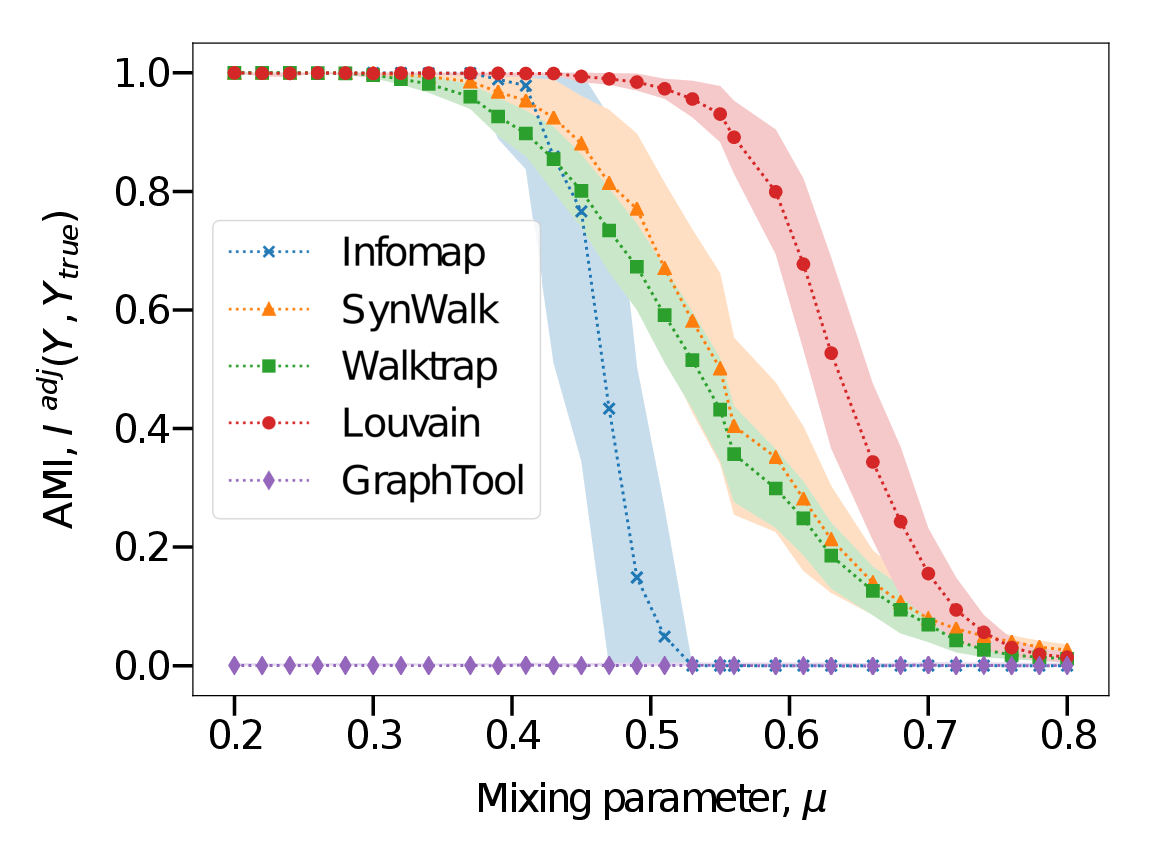
Complex systems, abstractly represented as networks, are ubiquitous in everyday life. Analyzing and understanding these systems requires, among others, tools for community detection. As no single best community detection algorithm can exist, robustness across a wide variety of problem settings is desirable. In this work, we present Synwalk, a random walk-based community detection method. Synwalk builds upon a solid theoretical basis and detects communities by synthesizing the random walk induced by the given network from a class of candidate random walks. We thoroughly validate the effectiveness of our approach on synthetic and empirical networks, respectively, and compare Synwalk’s performance with the performance of Infomap and Walktrap (also random walk-based), Louvain (based on modularity maximization) and stochastic block model inference. Our results indicate that Synwalk performs robustly on networks with varying mixing parameters and degree distributions. We outperform Infomap on networks with high mixing parameter, and Infomap and Walktrap on networks...
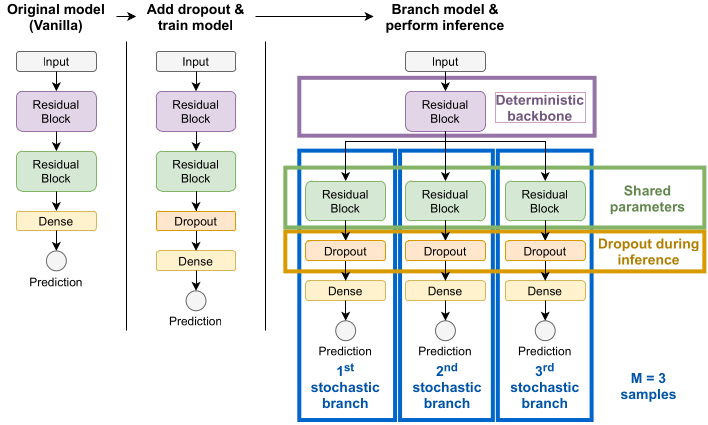
Uncertainty estimation and out-of-distribution robustness are vital aspects of modern deep learning. Predictive uncertainty supplements model predictions and enables improved functionality of downstream tasks including various resource-constrained embedded and mobile applications. Popular examples are virtual reality (VR), augmented reality (AR), sensor fusion, perception, and health applications including fitness indicators, arrhythmia detection, and skin lesion detection. Robust and reliable predictions with uncertainty estimates are increasingly important when operating on noisy in-the-wild data from sensory inputs. A large variety of deep learning architectures have been applied to various tasks with great success in terms of prediction quality, however, producing reliable and robust uncertainty without additional computational and memory overhead remains a challenge. This issue is further aggravated due to the limited computational and memory budget available in typical battery-powered mobile devices. In this paper, we aim to investigate more resource-efficient methods for uncertainty estimation that also provide good performance and robustness under...
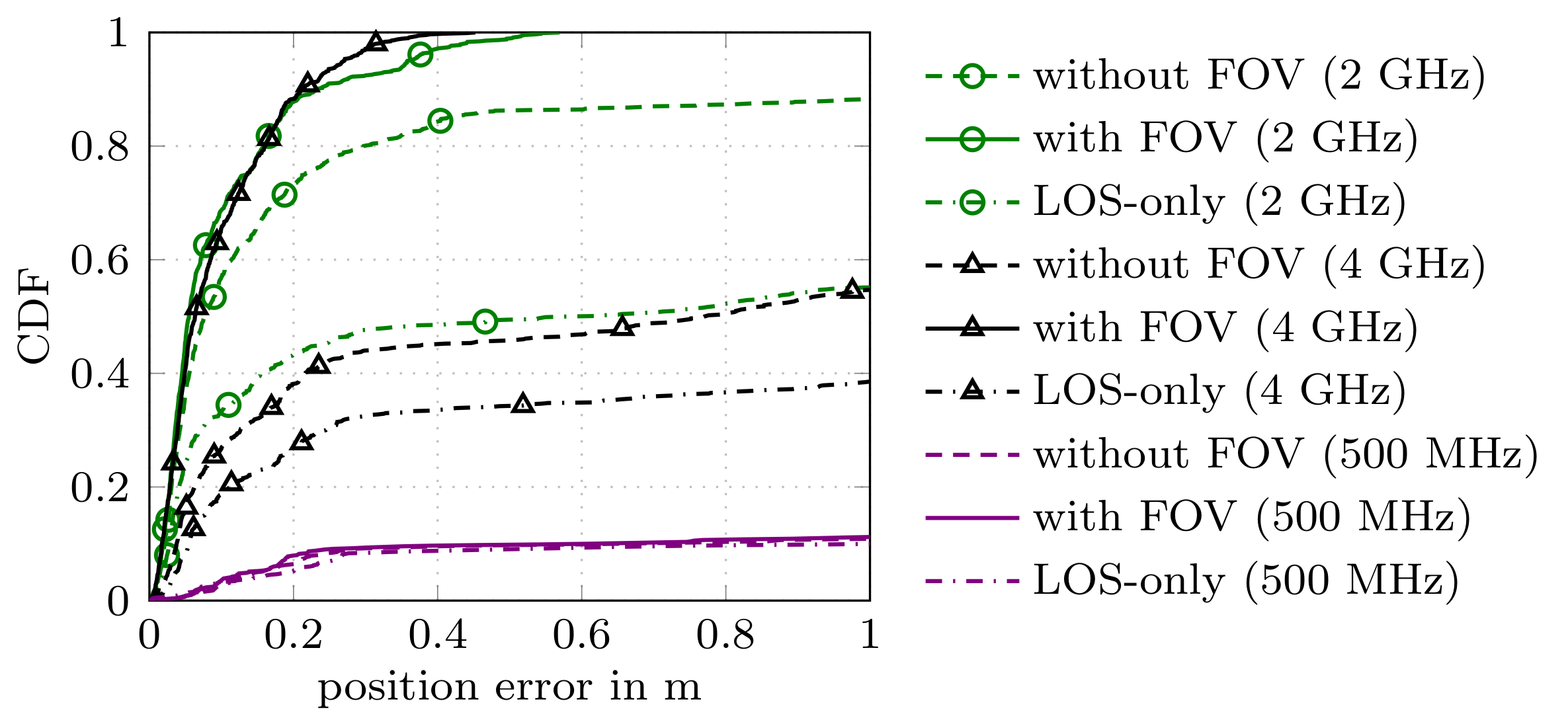
In this work we consider multipath-based positioning and tracking in off-body channels. We analyse the effects introduced by the human body and the resulting effects that are of interest in positioning and tracking based on channel measurements obtained in an indoor scenario. As the signal bandwidth is known to effect the achievable accuracy in positioning, the bandwidth dependency of the field of view (FOV) induced by human body via shadowing and the number of multipath components (MPCs) detected and estimated by a deterministic maximum likelihood (ML) algorithm is investigated. A multipath-based positioning and tracking algorithm is proposed that associates estimated MPC parameters with floor plan features and exploits a human body-dependent FOV function. The proposed algorithm is able to provide accurate position estimates even for an off-body radio channel in a multipath-prone environment with the signal bandwidth found to be a limiting factor. The figure shows the CDFs for the...
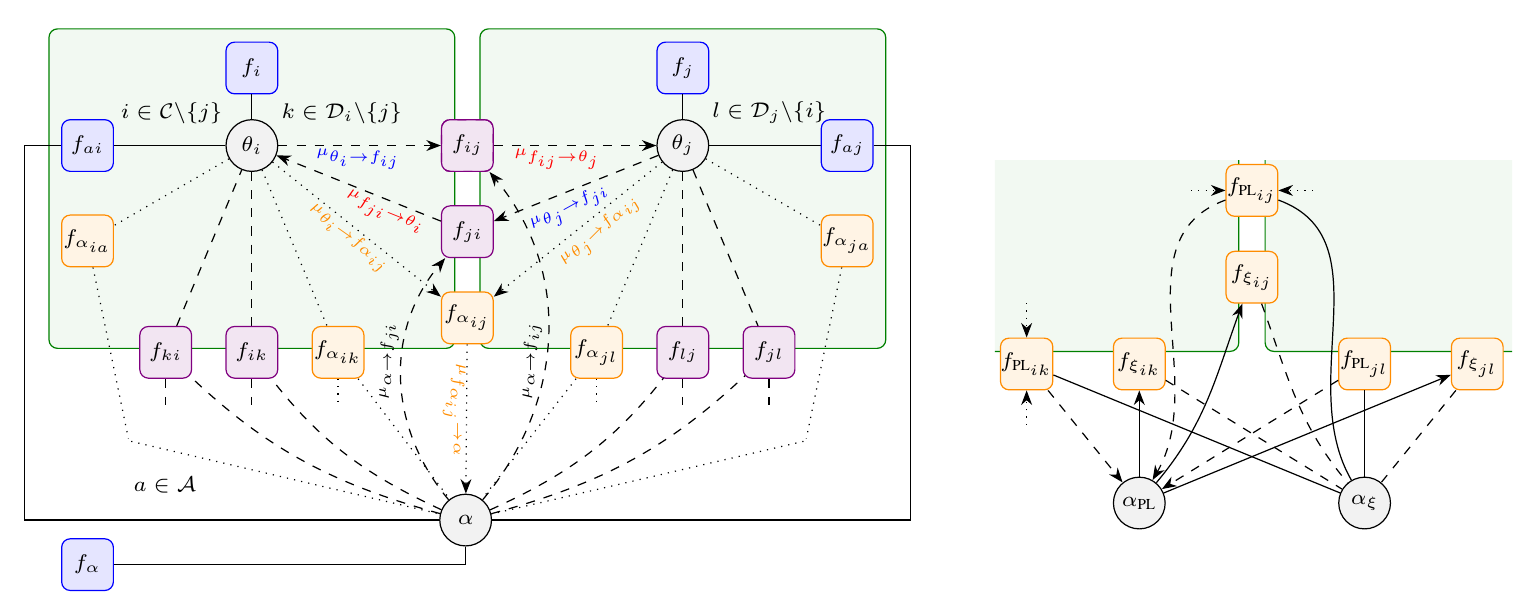
In cooperative localization applications, measurement-model related model parameters are often assumed to be known even though they can depend strongly on the environment. This assumption can lead to a reduced localization accuracy due to parameter mismatch. In this paper, we propose an adaptive factor-graph-based algorithm for joint cooperative localization and orientation estimation which inherently estimates all unknown model parameters as well as the measurement uncertainty. We use RSS radio measurements and account for the directivity of the antennas with a parametric antenna pattern. We validate our proposed methods with simulations in a static scenario and show that there is only a small loss in positioning accuracy compared to known model parameters and measurement noise. Figure: This figure shows a FG for joint cooperative localization and model parameter estimation. The left Figure shows the FG where all model parameters are captured in one node whereas the left figure shows how variable...
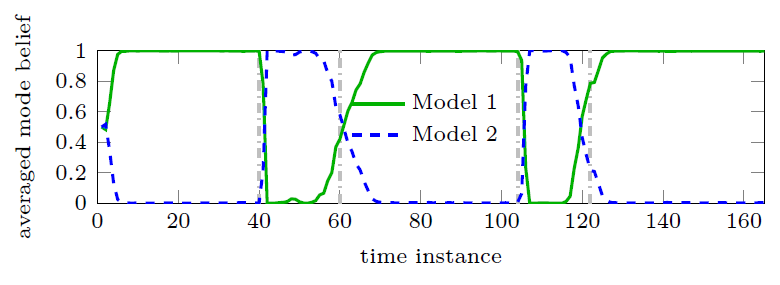
In this work, we present a Bayesian multipath-based simultaneous localization and mapping (SLAM) algorithm that continuously adapts interacting multiple models (IMM) parameters to describe the mobile agent state dynamics. The time-evolution of the IMM parameters is described by a Markov chain and the parameters are incorporated into the factor graph structure that represents the statistical structure of the SLAM problem. The proposed belief propagation (BP)-based algorithm adapts, in an online manner, to time-varying system models by jointly inferring the model parameters along with the agent and map feature states. The performance of the proposed algorithm is finally evaluating with a simulated scenario. Our numerical simulation results show that the proposed multipath-based SLAM algorithm is able to cope with strongly changing agent state dynamics. The full version of this paper can be found on Arxiv and on IEEE Xplore IEEE Xplore.

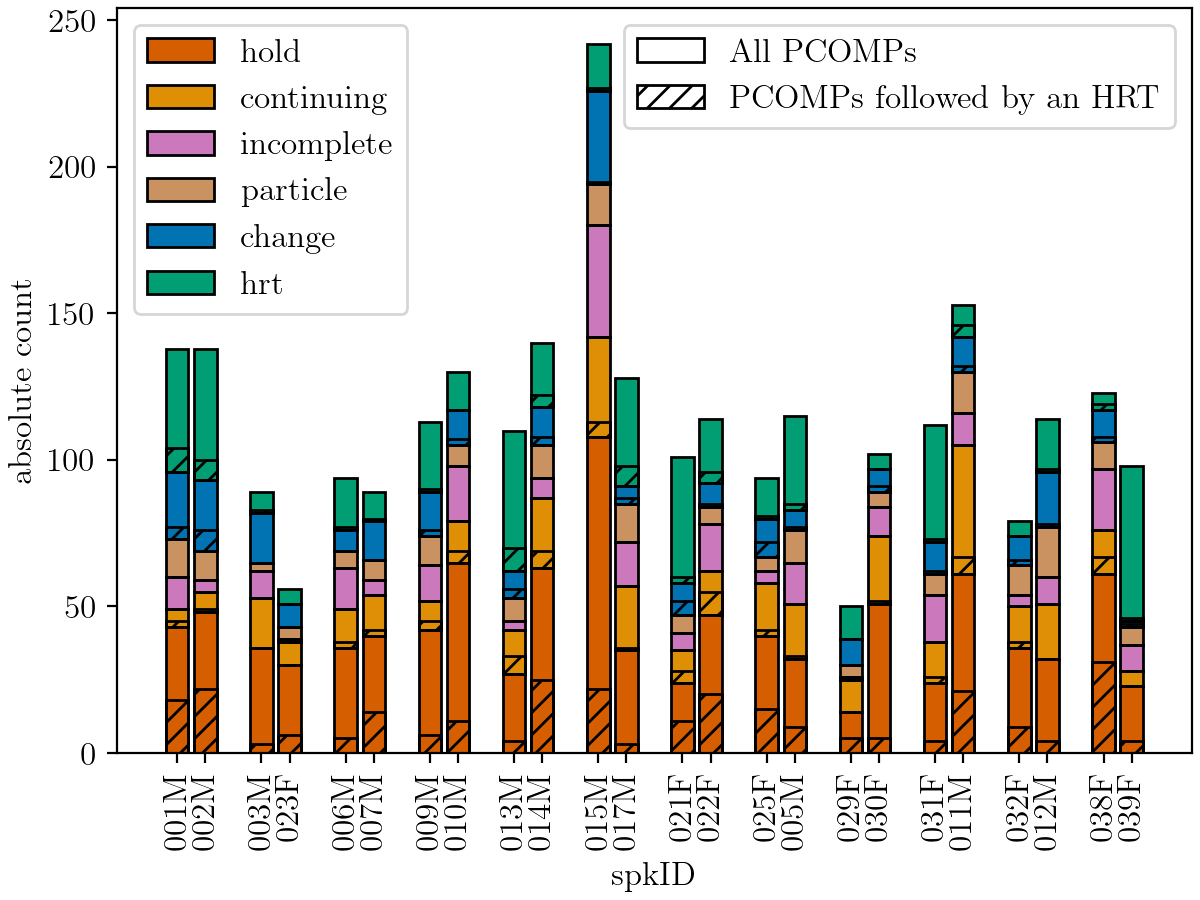
The investigation of conversational speech requires the close collaboration of linguists and speech technologists to develop new modeling techniques that allow the incorporation of various knowledge sources. This paper presents a progress report on the ongoing interdisciplinary project “Cross-layer language models for conversational speech” with a focus on the development of an annotation system for communicative functions. We discuss the requirements of such a system for the application in ASR as well as for the use in phonetic studies of talk-in-interaction, and illustrate emerging issues with the example of turn management. Our annotation system on the communicative functions level has two independent tiers. The IPU tier (“Inter Pausal Units”) and the PCOMP tier (“Points of potential syntactic COMPletion”). The figure shows an example of how PCOMP and IPU annotations are mapped onto each other. In this example, Speaker 2 holds his turn by making a pause at a point of...
This work provides an initial investigation on the application of convolutional neural networks (CNNs) for fingerprint-based positioning using measured massive MIMO channels. When represented in appropriate domains, massive MIMO channels have a sparse structure which can be efficiently learned by CNNs for positioning purposes. We evaluate the positioning accuracy of state-of-the-art CNNs with channel fingerprints generated from a channel model with a rich clustered structure: the COST 2100 channel model. We find that moderately deep CNNs can achieve fractional-wavelength positioning accuracies, provided that an enough representative data set is available for training. The full version of this paper can be found on Arxiv or on IEEE Xplore.
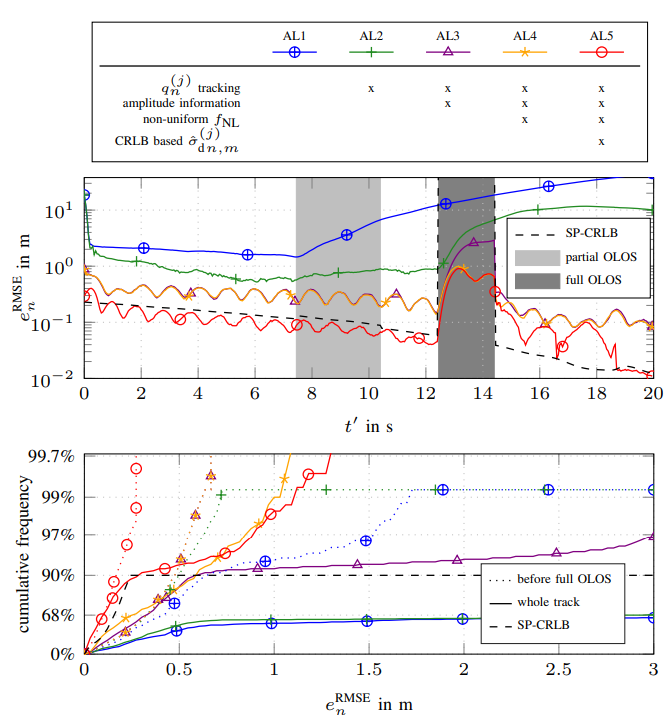
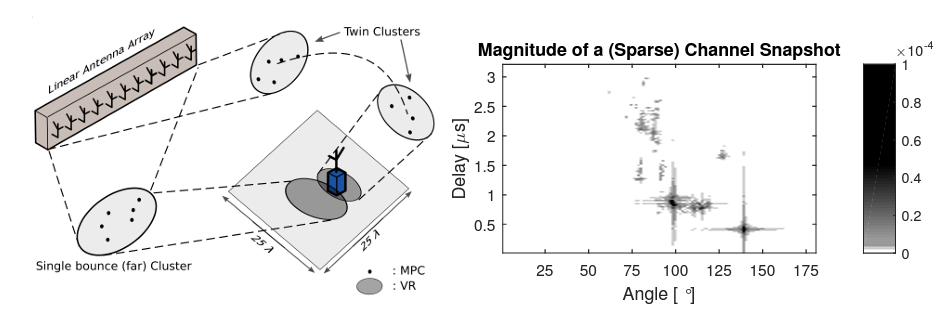
We present a message passing algorithm for localization and tracking in multipath-prone environments that implicitly considers obstructed line-of-sight situations. The proposed adaptive probabilistic data association algorithm infers the position of a mobile agent using multiple anchors by utilizing delay and amplitude of the multipath components (MPCs) as well as their respective uncertainties. By employing a nonuniform clutter model, we enable the algorithm to facilitate the position information contained in the MPCs to support the estimation of the agent position without exact knowledge about the environment geometry. Our algorithm adapts in an online manner to both, the time-varying signal-to-noise-ratio and line-of-sight (LOS) existence probability of each anchor. In a numerical analysis we show that the algorithm is able to operate reliably in environments characterized by strong multipath propagation, even if a temporary obstruction of all anchors occurs simultaneously The full version of this paper can be found on Arxiv or on...
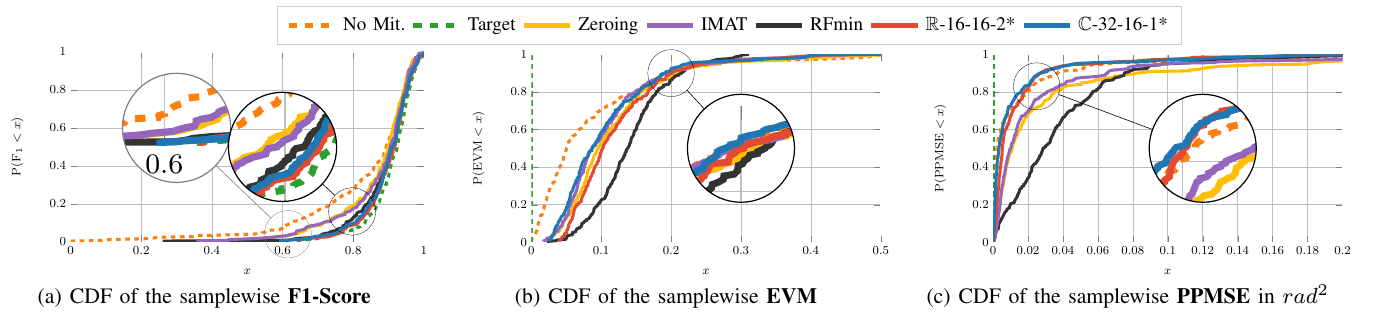
Autonomous driving highly depends on capable sensors to perceive the environment and to deliver reliable information to the vehicles’ control systems. To increase its robustness, a diversified set of sensors is used, including radar sensors. Radar is a vital contribution of sensory information, providing high resolution range as well as velocity measurements. The increased use of radar sensors in road traffic introduces new challenges. As the so far unregulated frequency band becomes increasingly crowded, radar sensors suffer from mutual interference between multiple radar sensors. This interference must be mitigated in order to ensure a high and consistent detection sensitivity. In this paper, we propose the use of Complex-valued Convolutional Neural Networks (CVCNNs) to address the issue of mutual interference between radar sensors. We extend previously developed methods to the complex domain in order to process radar data according to its physical characteristics. This not only increases data efficiency, but also...
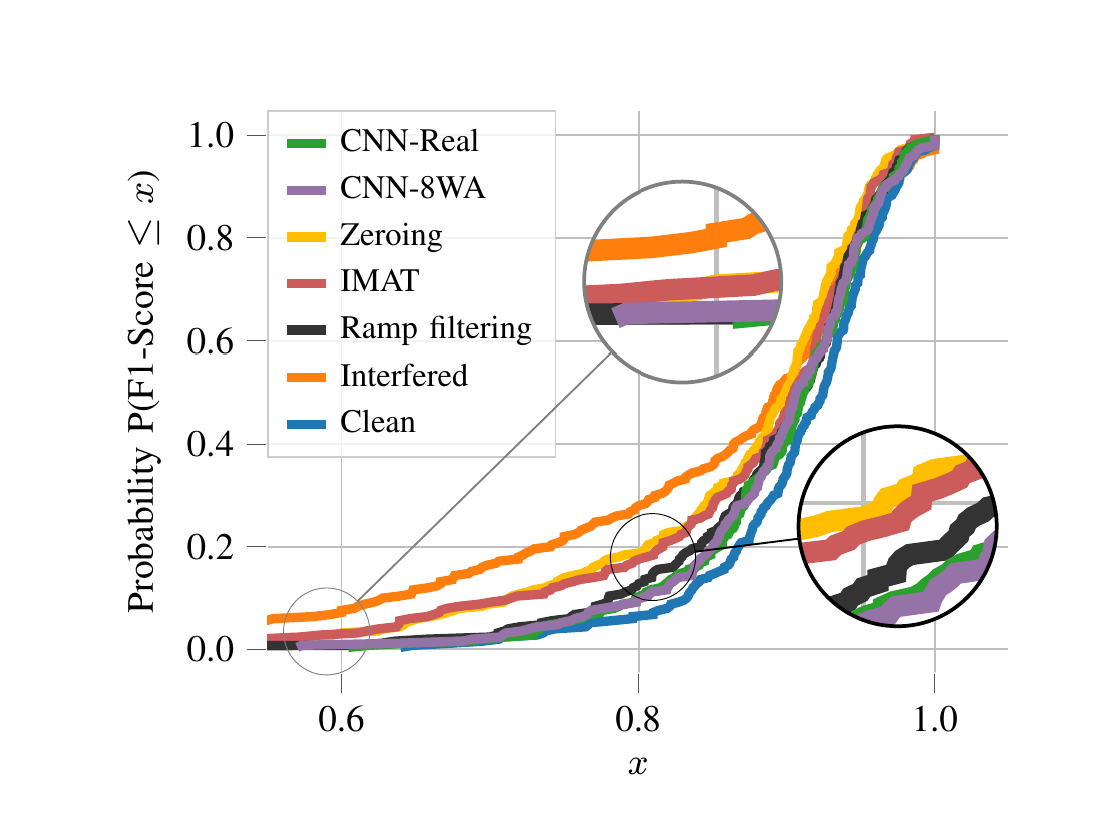
Radar sensors are crucial for environment perception of driver assistance systems as well as autonomous vehicles. Key performance factors are weather resistance and the possibility to directly measure velocity. With a rising number of radar sensors and the so-far unregulated automotive radar frequency band, mutual interference is inevitable and must be dealt with. Algorithms and models operating on radar data in early processing stages are required to run directly on specialized hardware, i.e. the radar sensor. This specialized hardware typically has strict resource constraints, i.e. a low memory capacity and low computational power. Convolutional Neural Network (CNN)-based approaches for denoising and interference mitigation yield promising results for radar processing in terms of performance. However, these models typically contain millions of parameters, stored in hundreds of megabytes of memory, and require additional memory during execution. In this paper, we investigate quantization techniques for CNN-based denoising and interference mitigation of radar signals....
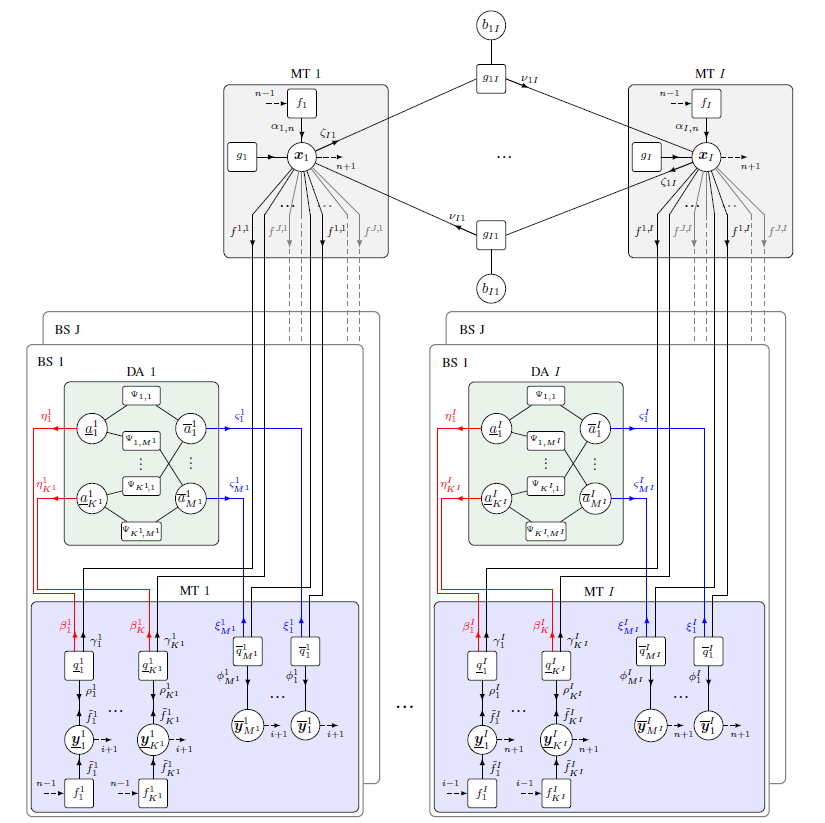
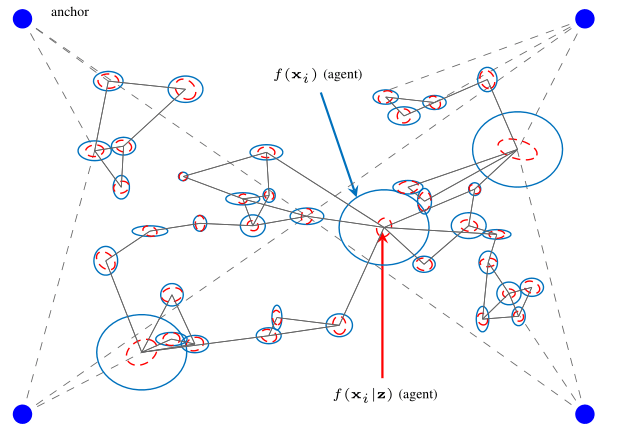
Multipath-based simultaneous localization and mapping (SLAM) algorithms can detect and localize radio reflective surfaces and jointly estimate the time-varying position of mobile agents. A promising approach is to represent radio reflective surfaces by so called virtual anchors (VAs). In existing multipathbased SLAM algorithms, VAs are modeled and inferred for each physical anchor (PA) and each propagation path individually, even if multiple VAs represent the same physical surface. This limits timeliness and accuracy of mapping and agent localization. In this paper, we introduce an improved statistical model and estimation method that enables data fusion for multipath-based SLAM by representing each surface with a single master virtual anchor (MVA). Our numerical simulation results show that the proposed multipath-based SLAM algorithm can significantly increase map convergence speed and reduce the mapping error compared to a state-of-the-art method. Figure: Factor graph for multipath-based SLAM corresponding to the factorization of the posterior PDF. Factor nodes...
We consider the problem of detecting and estimating radio channel dispersion parameters of a single specular multipath component (SMC) embedded in spatially correlated noise from observations collected using a MIMO measurement setup. The corresponding detection threshold versus the false alarm probability is derived from $\chi^2$-random field with two degrees of freedom defined over a 5-dimensional dispersion space using the theoretical framework of the expected Euler characteristic of random excursion sets. We show that the probability of false alarm is in excellent accordance with the relative-frequency of estimating false alarms using a maximum likelihood estimator and detector for acquiring the 5-dimensional dispersion parameter vector of the SMC. Figure: Results for data generated for a MIMO setup. Comparison of the derived probability of false alarm to the relative frequency of false alarm and a classical bin-based probability of false alarm, and the derived probability of missed detection to the relative frequency of...
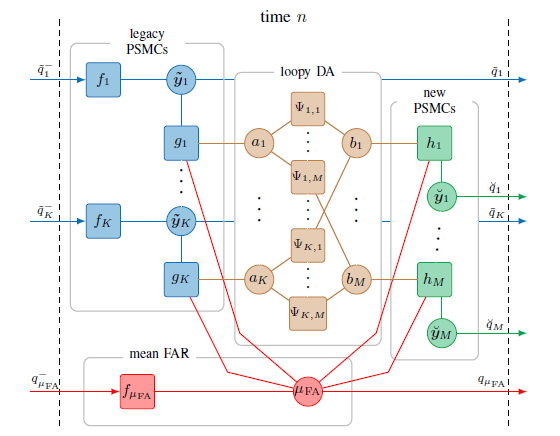
In this work we present a belief propagation (BP) algorithm with probabilistic data association (DA) for detection and tracking of specular multipath components (MPCs). In real dynamic measurement scenarios, the number of MPCs reflected from visible geometric features, the MPC dispersion parameters, and the number of false alarm contributions are unknown and time-varying. We develop a Bayesian model for specular MPC detection and joint estimation problem, and represent it by a factor graph which enables the use of BP for efficient computation of the marginal posterior distributions. A parametric channel estimator is exploited to estimate at each time step a set of MPC parameters, which are further used as noisy measurements by the BP-based algorithm. The algorithm performs probabilistic DA, and joint estimation of the time-varying MPC parameters and mean false alarm rate. Preliminary results using synthetic channel measurements demonstrate the excellent performance of the proposed algorithm in a realistic...
Learning the structure of Bayesian networks is a difficult combinatorial optimization problem. In this paper, we consider learning of tree-augmented naive Bayes (TAN) structures for Bayesian network classifiers with discrete input features. Instead of performing a combinatorial optimization over the space of possible graph structures, the proposed method learns a distribution over graph structures. After training, we select the most probable structure of this distribution. This allows for a joint training of the Bayesian network parameters along with its TAN structure using gradient-based optimization. The proposed method is agnostic to the specific loss and only requires that it is differentiable. We perform extensive experiments using a hybrid generative-discriminative loss based on the discriminative probabilistic margin. Our method consistently outperforms random TAN structures and Chow-Liu TAN structures. The paper was presented at the International Conference on Probabilistic Graphical Models (PGM 2020) and can be found at https://arxiv.org/abs/2008.09566. Code for the experiments...
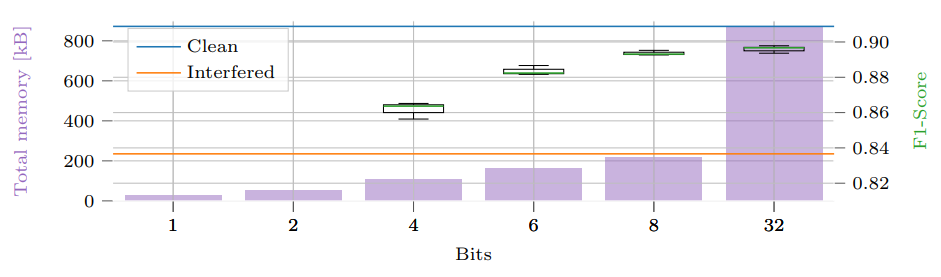
Radar sensors are crucial for environment perception of driver assistance systems as well as autonomous vehicles. Key performance factors are weather resistance and the possibility to directly measure velocity. With a rising number of radar sensors and the so far unregulated automotive radar frequency band, mutual interference is inevitable and must be dealt with. Algorithms and models operating on radar data in early processing stages are required to run directly on specialized hardware, i.e. the radar sensor. This specialized hardware typically has strict resource-constraints, i.e. a low memory capacity and low computational power. Convolutional Neural Network (CNN)-based approaches for denoising and interference mitigation yield promising results for radar processing in terms of performance. However, these models typically contain millions of parameters, stored in hundreds of megabytes of memory, and require additional memory during execution. In this paper we investigate quantization techniques for CNN-based denoising and interference mitigation of radar signals....
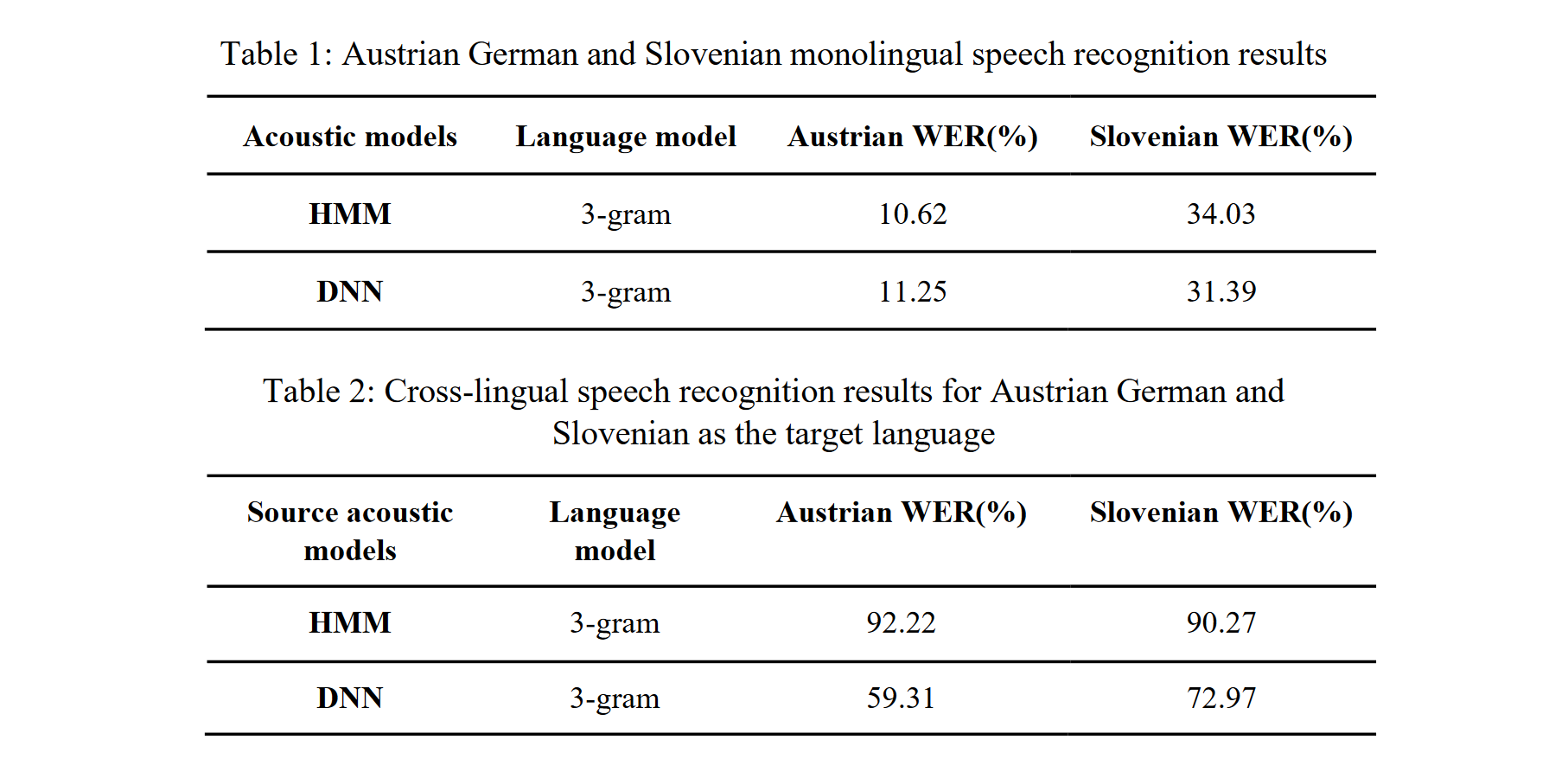
Methods of cross-lingual speech recognition have a high potential to overcome limitations on resources of spoken language in under-resourced languages. Not only can they be applied to build automatic speech recognition (ASR) systems for such languages, they can also be utilized to generate further resources of spoken language. This paper presents a cross-lingual ASR system based on data from two languages, Slovenian and Austrian German. Both were used as a source and target language for cross-lingual transfer (i.e., the acoustic models were trained on material from the source language, and recognition was tested on material from the target language). The cross-lingual mapping between the Slovenian phone set (40 phones) and the Austrian German phone set (33 phones) was carried out using expert knowledge about the acoustic-phonetic properties of the phones. For the experiments, we used data from two speech corpora: the Slovenian BNSI Broadcast News speech database and the Austrian...
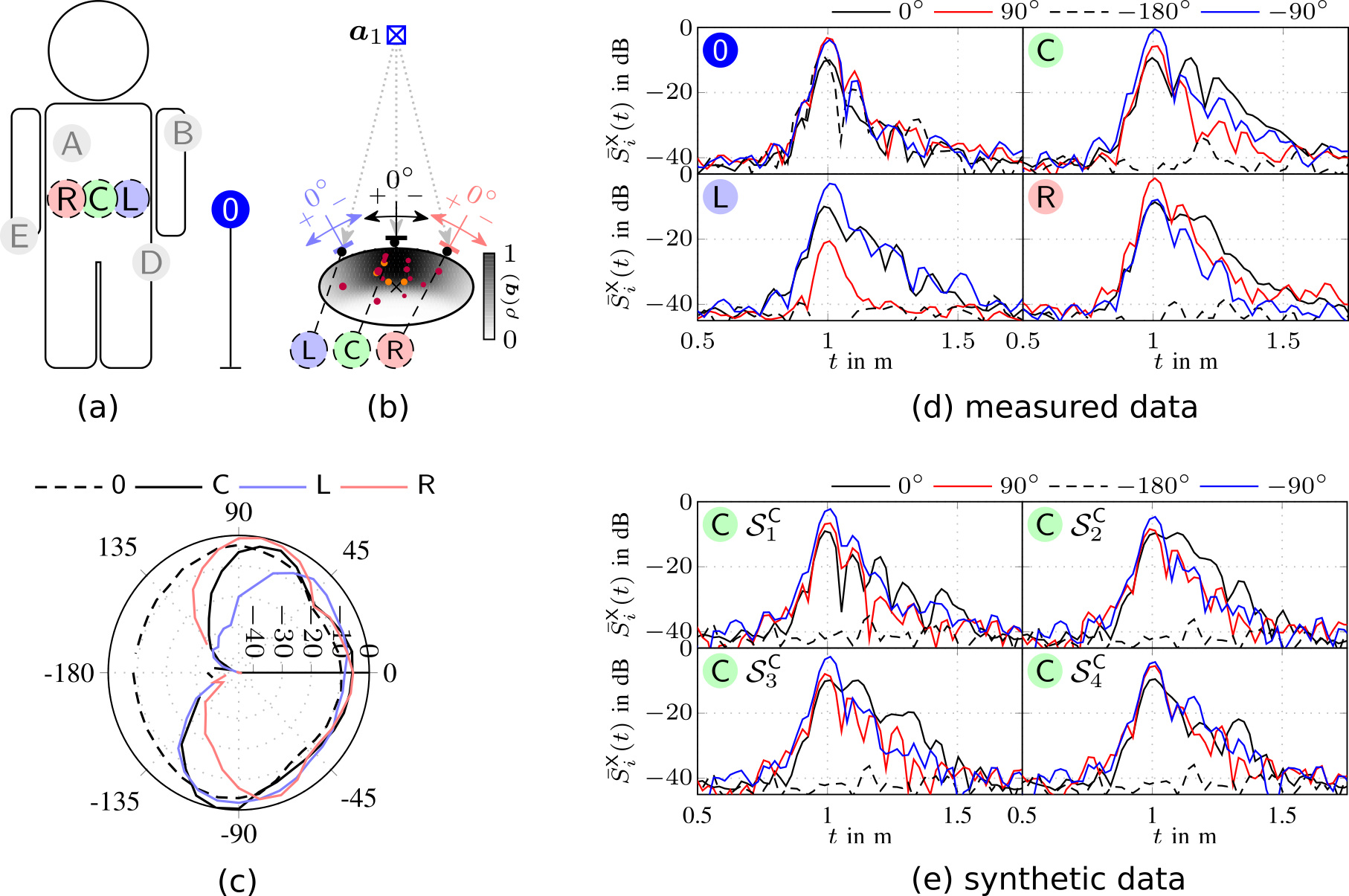
In this paper we describe a simple and intuitive model for the effects of the human body of a user close by a receiver. We specifically investigate the UWB channel in off-body condition, where the agent device is located directly on the human body, and another device functioning as anchor is located in the environment. Due to the high time resolution of UWB signals, the effect of the human body can be modeled by means of a extended object producing multiple scattered paths. The geometric stochastic channel model is based on a connection between an (empirically chosen) ellipsoidal body shape and a distribution function for the scattering points chosen to fit measurements in terms of the resulting signal shape as well as in terms of the effects visible when applying a maximum likelihood multipath channel estimator. The effect of the human body manifests itself most notably via strong shadowing, climaxing...
This work, we investigate the reliability of time-of-arrival (TOA) based ranging using maximum-likelihood (ML) estimation in a dense multipath (DM) channel in terms of both the conventional mean squared error (MSE) as well as confidence bounds. We show that in the presence of DM the ML estimator distorts the signal mainlobe due to its whitening property, resulting in a bandwidth (BW) dependent bias, even before the outlier driven threshold region is reached. Low-complexity metrics for accurately determining the performance in terms of the probability density (PDF) of the estimation error of both ML estimation and joint ML estimation and detection are provided. These metrics are based on the well known method of interval estimation (MIE) combined with local error prediction using the normalized noise-free likelihood (NNLIKE) and consider the non-Gaussian effects of outliers as well as mainlobe distortion. The full version of the paper can be found on Researchgate Figure:...
In this work, we propose a Bayesian agent network planning algorithm for information-criterion-based measurement selection for cooperative localization in static networks with anchors. This allows to increase the accuracy of the agent positioning while keeping the number of measurements between agents to a minimum. The proposed algorithm is based on minimizing the conditional differential entropy (CDE) of all agent states to determine the optimal set of measurements between agents. Such combinatorial optimization problems have factorial runtime and quickly become infeasible, even for a rather small number of agents. Therefore, we propose a Bayesian agent network planning algorithm that performs a local optimization for each state. Experimental results demonstrate a performance improvement compared to a random measurement selection strategy, significantly reducing the position RMSE at a smaller number of measurements between agents. The full version of the paper can be found on Researchgate Figure: This figure shows a scenario of a...
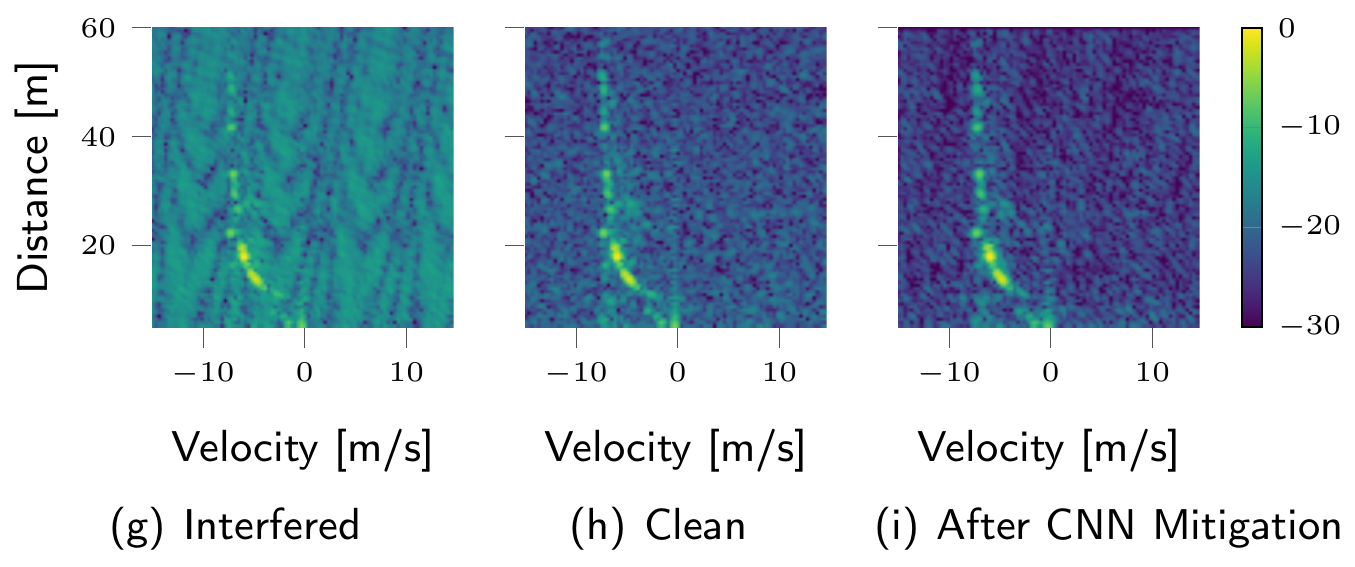
Radar sensors are crucial for environment perception of driver assistance systems as well as autonomous cars. Key performance factors are a fine range resolution and the possibility to directly measure velocity. With a rising number of radar sensors and the so far unregulated automotive radar frequency band, mutual interference is inevitable and must be dealt with. Sensors must be capable of detecting, or even mitigating the harmful effects of interference, which include a decreased detection sensitivity. In this paper, we evaluate a Convolutional Neural Network (CNN)-based approach for interference mitigation on real-world radar measurements. We combine real measurements with simulated interference in order to create input-output data suitable for training the model. A finite sample size performance comparison shows the effectiveness of the model trained on either simulated or real data as well as for transfer learning. A comparative performance analysis with the state of the art emphasizes the potential...

Computational methods for the analysis of lung sounds are beneficial for computer-supported diagnosis, digital storage and monitoring in critical care. Pathological changes of the lung are tightly connected to characteristic sounds enabling a fast and inexpensive diagnosis. Traditional auscultation with a stethoscope has several disadvantages: subjectiveness, i.e. the lung sounds are evaluated depending on the experience of the physician, cannot provide continuous monitoring and a trained expert is required. Furthermore, the characteristics of the sounds are in the low frequency range, where the human hearing has limited sensitivity and is susceptible to noise artifacts. To facilitate a more objective assessment of the lung sounds for diagnosis of pulmonary diseases/conditions we developed a multi-channel recording device (see Figure). Furthermore, in a clinical trial we classified adventitious and normal lung sounds using deep neural networks [1]. Our device enables a reliable easy-to-use lung sound recording for (1) better assistance to patients and...
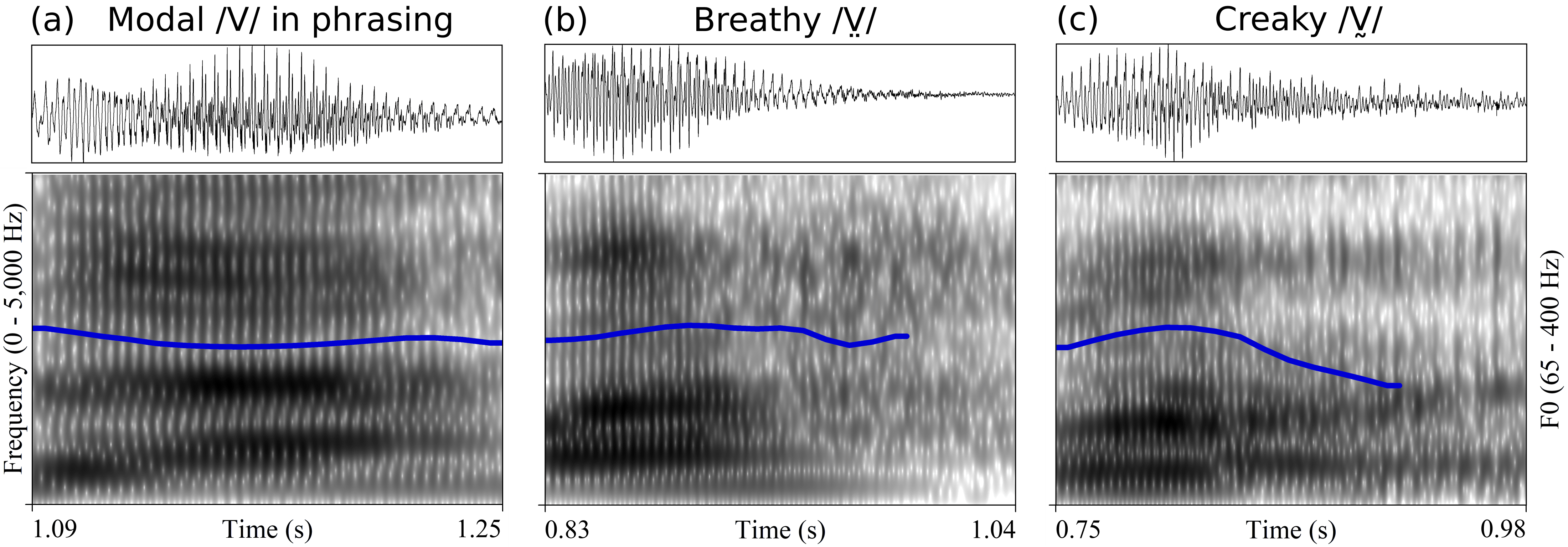
Chichimec (Otomanguean) has two tones, high and low, and a phonological three-way phonation contrast: modal /V/, breathy /V̤/ and creaky /V̰/. Tone and phonation type contrasts are used independently. This paper investigates the acoustic realization of modal, breathy and creaky vowels, the timing of phonation in non-modal vowels, and the production of tone in combination with different phonation types. The results of Cepstral Peak Prominence and three spectral tilt measures showed that phonation type contrasts are not distinguished by the same acoustic measures for women and men. In line with expectations for laryngeally complex languages, phonetic modal and non-modal phonation are sequenced in phonological breathy and creaky vowels. With respect to the timing pattern, however, the results show that non-modal phonation is not, as previously reported, mainly located in the middle of the vowel. Non-modal phonation is instead predominantly realized in the second half of phonological breathy and creaky vowels....
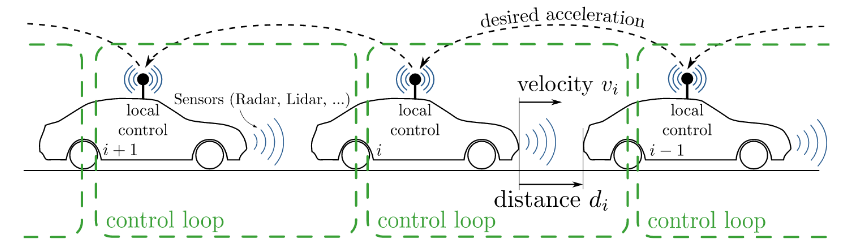
Models play an essential role in the design process of cyber-physical systems. They form the basis for simulation and analysis and help in identifying design problems as early as possible. However, the construction of models that comprise physical and digital behavior is challenging. Consequently, there is considerable interest in learning the behavior of such systems using machine learning. However, the performance of the machine learning techniques depends crucially on sufficient and representative training data covering the behavior of the system adequately not only in standard situations, but also in edge cases that are often particularly important. In this work, we successfully combine methods from automata learning and model-based testing to fully automatically generate training data that is rich of edge cases. Experimental results on a platooning scenario show that recurrent neural networks learned with this data achieved significantly better results compared to models learned from randomly generated data. In particular,...

Gaussian Processes (GPs) are powerful non-parametric Bayesian regression models that allow exact posterior inference, but exhibit high computational and memory costs. In order to improve scalability of GPs, approximate posterior inference is frequently employed, where a prominent class of approximation techniques is based on local GP experts. However, the local-expert techniques proposed so far are either not well-principled, come with limited approximation guarantees, or lead to intractable models. In this paper, we introduce deep structured mixtures of GP experts, a well-principled stochastic process model which i) allows exact posterior inference, ii) has attractive computational and memory costs, and iii), when used as GP approximation, captures predictive uncertainties consistently better than previous approximations. Furthermore, deep structured mixtures can optionally be fine-tuned locally – regularised using local similarity constraints – which enables modelling of heteroscedasticity and non-stationarities. In a variety of experiments, we show that deep structured mixtures have a low approximation...
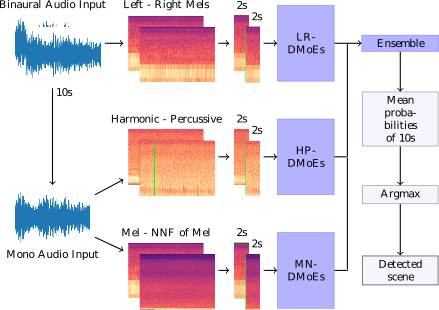
We propose a heterogeneous system of Deep Mixture of Experts (DMoEs) models using different Convolutional Neural Networks (CNNs) for acoustic scene classification (ASC). Each DMoEs module is a mixture of different parallel CNN structures weighted by a gating network. All CNNs use the same input data. The CNN architectures play the role of experts extracting a variety of features. The experts are pre-trained, and kept fixed (frozen) for the DMoEs model. The DMoEs is post-trained by optimizing weights of the gating network, which estimates the contribution of the experts in the mixture. In order to enhance the performance, we use an ensemble of three DMoEs modules each with different pairs of inputs and individual CNN models. The input pairs are spectrogram combinations of binaural audio and mono audio as well as their pre-processed variations using harmonic-percussive source separation (HPSS) and nearest neighbor filters (NNFs). The classification result of the proposed...
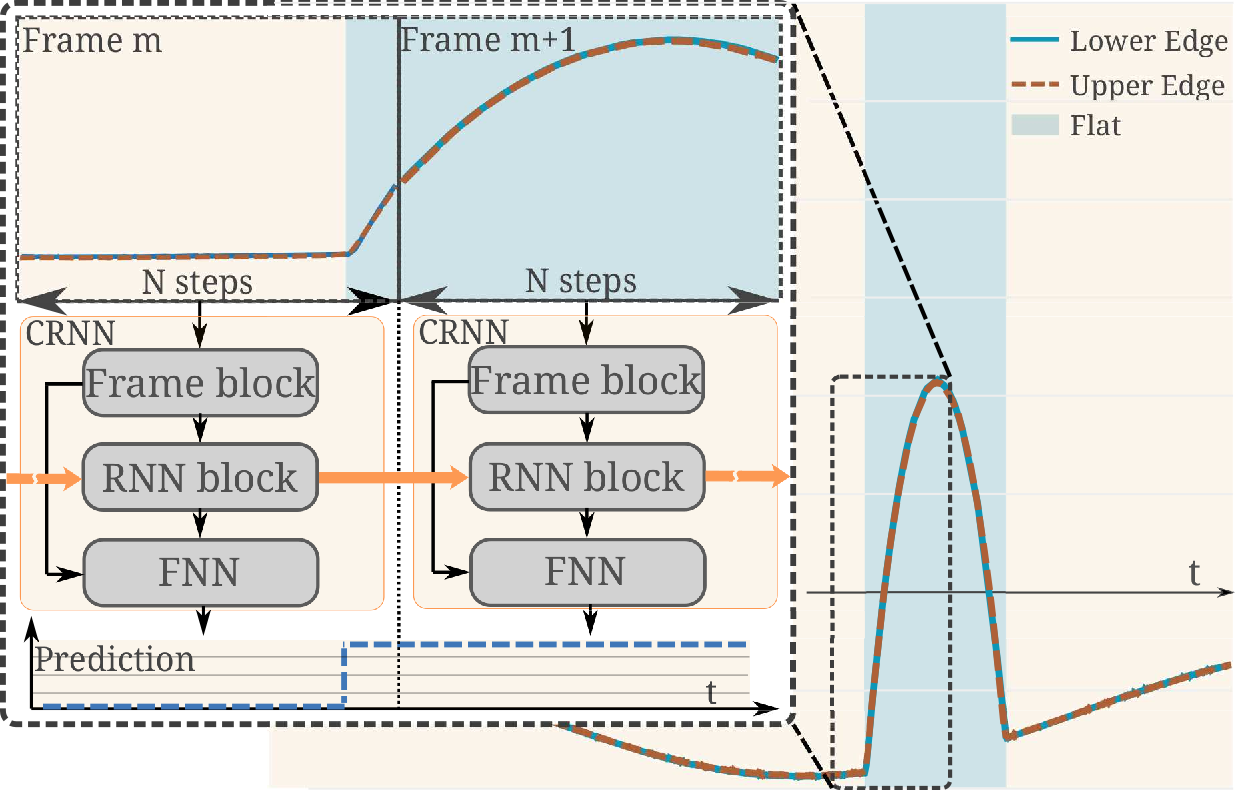
Efficient real-time segmentation and classification of time-series data is key in many applications, including sound and measurement analysis. We propose an efficient convolutional recurrent neural network (CRNN) architecture that is able to deliver improved segmentation performance at lower computational cost than plain RNN methods. We develop a CNN architecture, using dilated DenseNet-like kernels and implement it within the proposed CRNN architecture. For the task of online wafer-edge measurement analysis, we compare our proposed methods to standard RNN methods, such as Long Short Term Memory (LSTM) and Gated Recurrent Units (GRUs). We focus on small models with a low computational complexity, in order to run our model on an embedded device. We show that frame-based methods generally perform better than RNNs in our segmentation task and that our proposed recurrent dilated DenseNet achieves a substantial improvement of over 1.1 % F1-score compared to other frame-based methods. Figure: Principle of the recurrent...
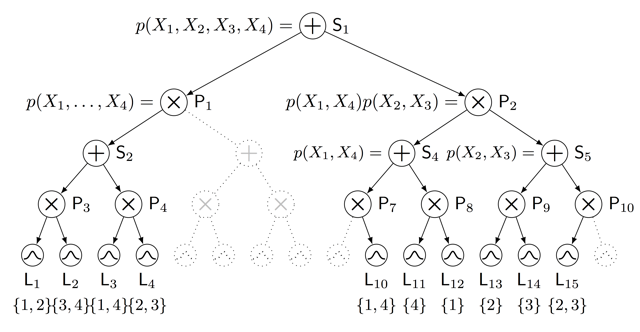
Sum-product networks (SPNs) are flexible density estimators and have received significant attention, due to their attractive inference properties. While parameter learning in SPNs is well developed, structure learning leaves something to be desired: Even though there is a plethora of SPN structure learners, most of them are somewhat ad-hoc, and based on intuition rather than a clear learning principle. In this paper, we introduce a well-principled Bayesian framework for SPN structure learning. First, we decompose the problem into i) laying out a basic computational graph, and ii) learning the so-called scope function over the graph. The first is rather unproblematic and akin to neural network architecture validation. The second characterises the effective structure of the SPN and needs to respect the usual structural constraints in SPN, i.e.~completeness and decomposability. While representing and learning the scope function is rather involved in general, in this paper, we propose a natural parametrisation for...
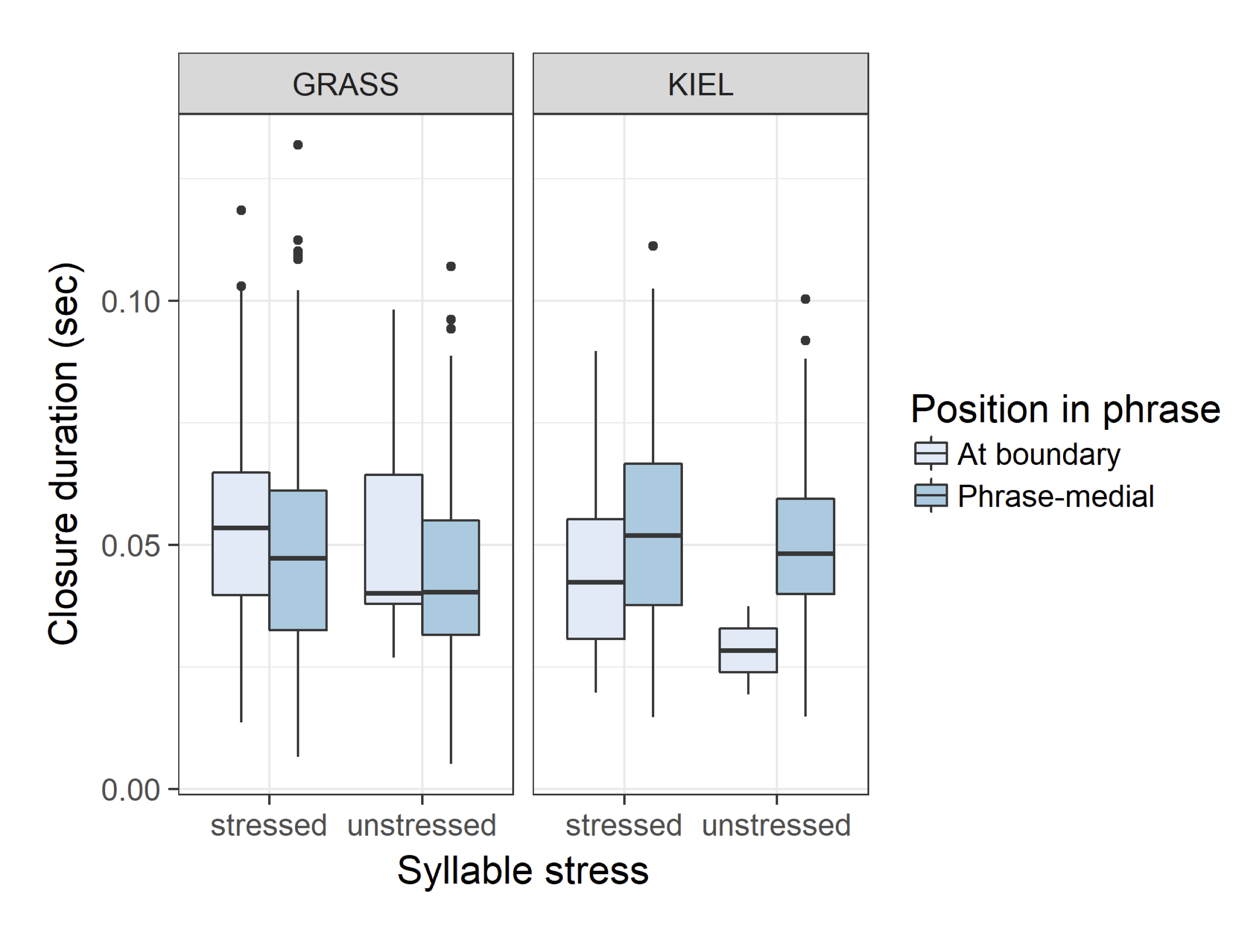
This study investigates the acoustic cues used to mark prosodic boundaries in two varieties of German, with a specific focus on variations in production of fortis and lenis plosives. Based on prosodic-boundary-adjacent and non-boundary-adjacent plosives from GRASS (Austrian German) and the Kiel Corpus of Read Speech (Northern German), we found that closure and burst duration features, as well as duration of a preceding adjacent segment,vary consistently in relationship to the presence or absence of a prosodic boundary, but that the relative weights of these features differ in the two varieties studied. Whereas stress marking in plosives is being driven more by burst duration in the Kiel Corpus data, it is driven more by closure duration in the GRASS data. This study suggests that boundary detection tools require variety-specific training materials, or else information from comparative studies such as the current work, in order to attain optimalfunction in specific varieties or...
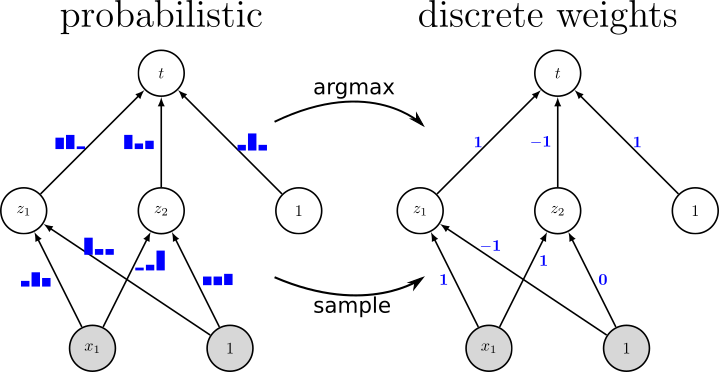
Since resource-constrained devices hardly benefit from the trend towards ever-increasing neural network (NN) structures, there is growing interest in designing more hardware-friendly NNs. In this paper, we consider the training of NNs with discrete-valued weights and sign activation functions that can be implemented more efficiently in terms of inference speed, memory requirements, and power consumption. We build on the framework of probabilistic forward propagations using the local reparameterization trick, where instead of training a single set of NN weights we rather train a distribution over these weights. Using this approach, we can perform gradient-based learning by optimizing the continuous distribution parameters over discrete weights while at the same time perform backpropagation through the sign activation. In our experiments, we investigate the influence of the number of weights on the classification performance on several benchmark datasets, and we show that our method achieves state-of-the-art performance. Figure: Instead of learning conventional real-valued...
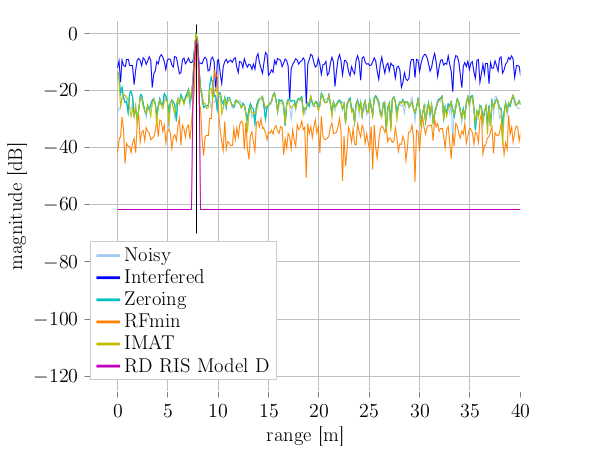
Automotive radar is used to perceive the vehicle’s environment due to its capability to measure distance, velocity and angle of surrounding objects with a high resolution. With an increasing number of deployed radar sensors on the streets and because of missing regulations of the automotive radar frequency band, mutual interference must be dealt with in order to retain a sensitive detection capability. In this work we analyze the capability of Convolutional Neural Networks (CNNs) to address the issue of interference mitigation. Since automotive radar is a safety-critical application, interference mitigation and denoising algorithms must fulfill certain requirements. Application-related performance metrics are used to analyze noise suppression capability and ensure that no artifacts are generated by the processing. In this paper we show how NN-based denoising can applied in different steps of the radar signal processing chain. show specific CNN structures capable of denoising radar signals. present numerical results using application-related...
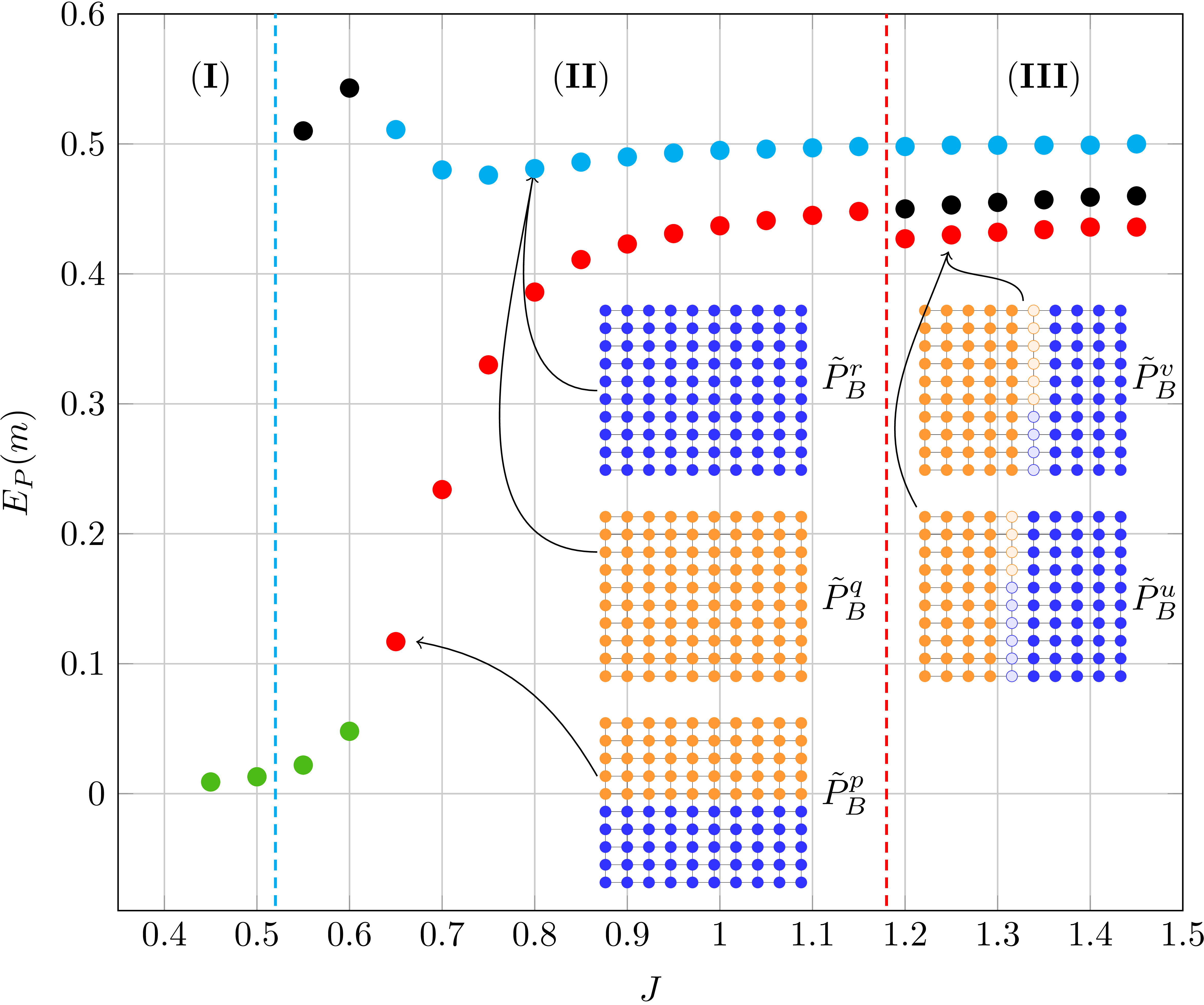
The marginals and the partition function can be estimated in a straight-forward manner for tree-structured models but require efficient approximation methods if the graphical model contains loops. One such method is Belief Propagation (BP) that exploits the structure of probabilistic graphical models in order to approximate the marginal distribution and the partition function. In this work, we analyze the difference between accurate marginals and an accurate partition function. Therefore, we go beyond well-established models (e.g., attractive models with identical or random potentials) and introduce a rich class of attractive models with inherent structure: patch potential models. These models exhibit many interesting phenomena and provide deep insights into the relationship between the approximation quality of the marginals and the partition function. We discuss the properties of the solution space and demonstrate that: (i) three different regions with fundamentally different properties exist; (ii) although it is often infeasible to obtain and combine...
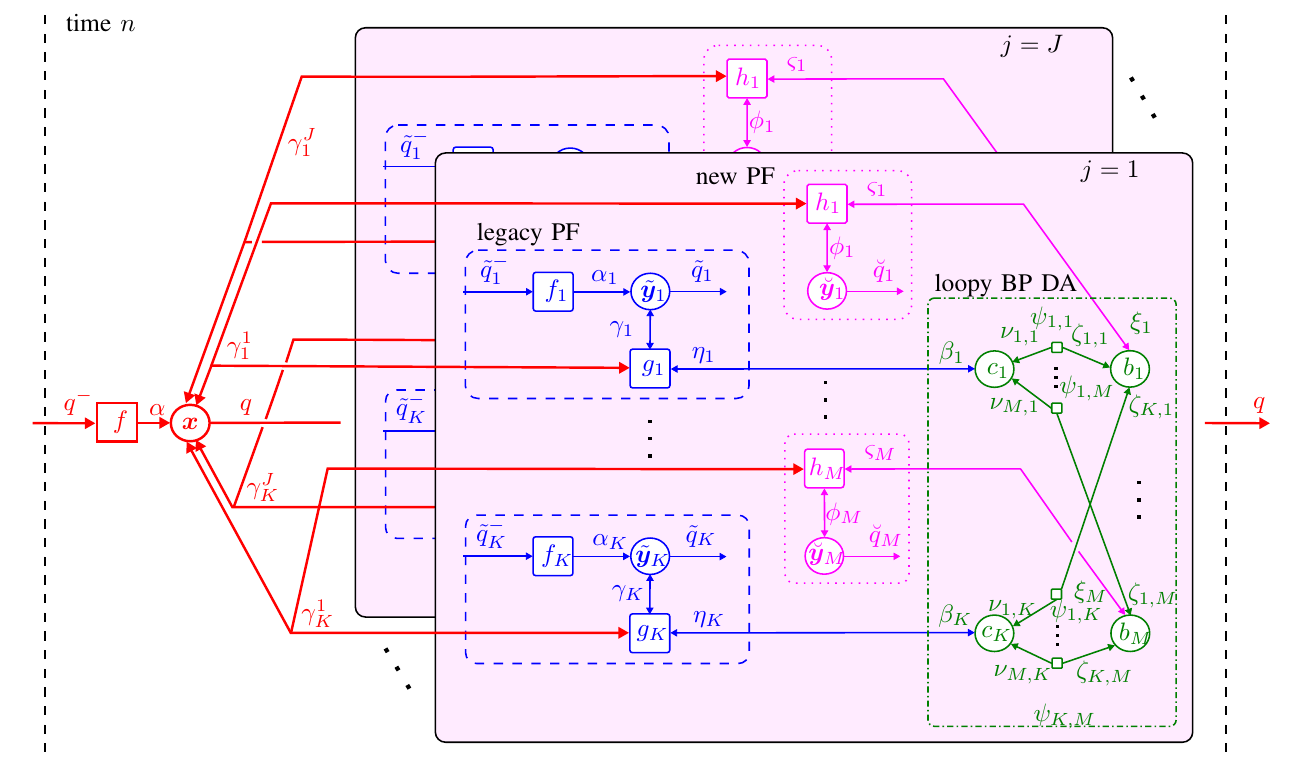
Simultaneous localization and mapping (SLAM) is important in many fields including robotics, autonomous driving, location-aware communication, and robust indoor localization. Specifically, robustness, i.e. achieving a low probability of localization outage, is still a challenging task in environments with strong multipath propagation. Therefore, new systems supporting multipath channels either take advantage of it by exploiting multipath components (MPCs) for localization [5], [6], [10], exploiting cooperation among agents, and/or exploiting robust signal processing against multipath propagation and clutter measurements in general. This work presents a Bayesian feature-based simultaneous localization and mapping (SLAM) algorithm that exploits multipath components (MPCs) in radio-signals. The proposed belief propagation (BP)-based algorithm enables the estimation of the position, velocity, and orientation of the mobile agent equipped with an antenna array by utilizing the delays and the angle-of-arrivals (AoAs) of the MPCs. The proposed algorithm also exploits the statistics of the complex amplitudes of MPC parameters, i.e. amplitude information...
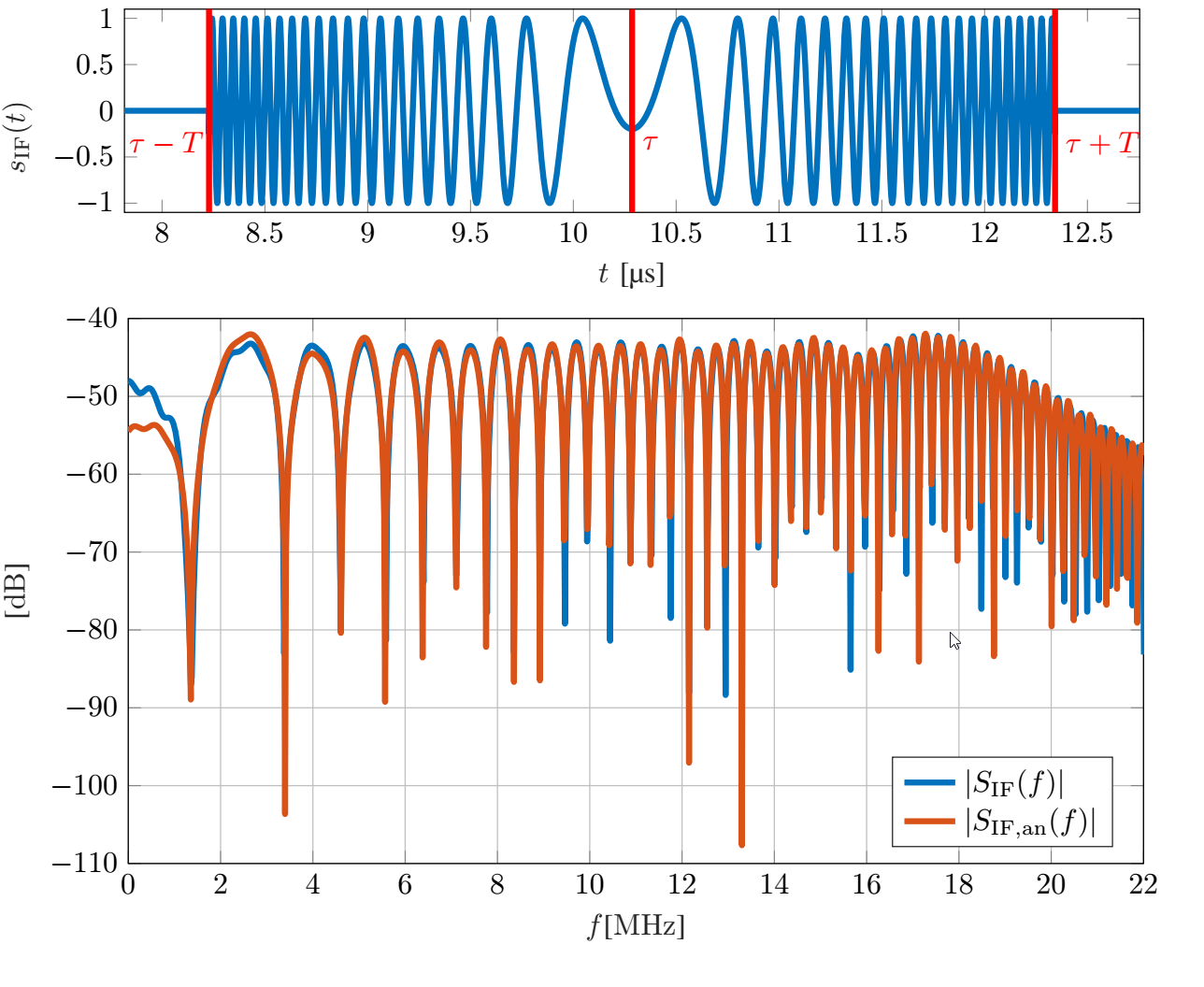
Radar sensors are increasingly utilized in today’s cars. This inevitably leads to increased mutual sensor interference and thus a performance decrease, potentially resulting in major safety risks. Understanding signal impairments caused by interference accurately helps to devise signal processing schemes to combat said performance degradation. For the FMCW radars prevalent in automotive applications, it has been shown that so-called non-coherent interference occurs frequently and results in an increase of the noise floor. In this work we investigate the impact of interference analytically by focusing on its detailed description. We show, among others, that the spectrum of the typical interference signal has a linear phase and a magnitude that is strongly fluctuating with the phase parameters of the time domain interference signal. Analytical results are verified by simulation, highlighting the dependence on the specific phase terms that cause strong deviations from spectral whiteness. Figure: The upper plot depicts an example of...
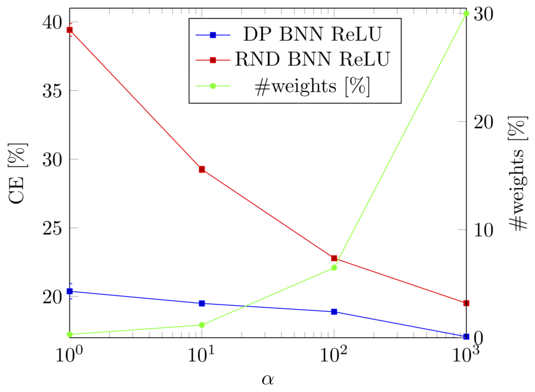
We extend feed-forward neural networks with a Dirichlet process prior over the weight distribution. This enforces a sharing on the network weights, which can reduce the overall number of parameters drastically. We alternately sample from the posterior of the weights and the posterior of assignments of network connections to the weights. This results in a weight sharing that is adopted to the given data. In order to make the procedure feasible, we present several techniques to reduce the computational burden. Experiments show that our approach mostly outperforms models with random weight sharing. Our model is capable of reducing the memory footprint substantially while maintaining a good performance compared to neural networks without weight sharing. Figure: The concentration parameter alpha of the Dirichlet processes can be used to trade-off between the classification error (CE) and the memory requirements of the model, i.e., how many weights are shared. Especially if only a...
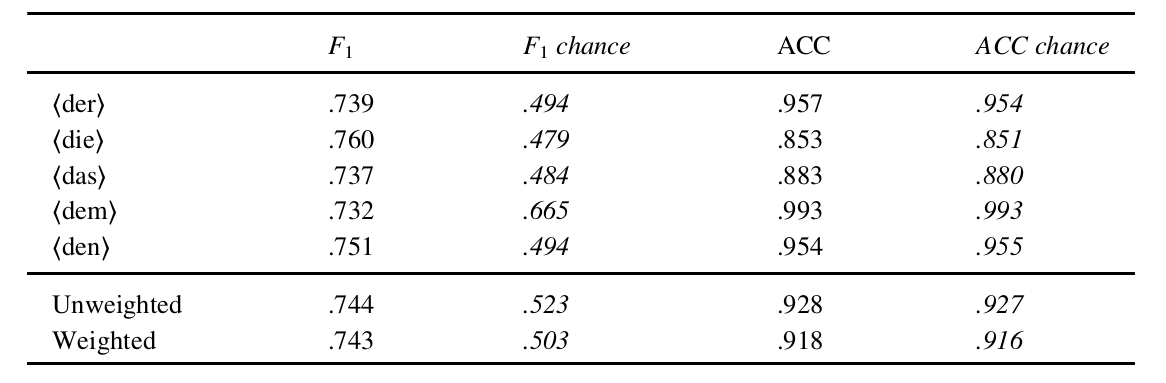
Homophones pose serious issues for automatic speech recognition (ASR) as they have the same pronunciation but different meanings or spellings. Homophone disambiguation is usually done within a stochastic language model or by an analysis of the homophonous word’s context. Whereas this method reaches good results in read speech, it fails in conversational, spontaneous speech, where utterances are often short, contain disfluencies and/or are realized syntactically incomplete. Phonetic studies have shown that words that are homophonous in read speech often differ in their phonetic detail in spontaneous speech. Whereas humans use phonetic detail to disambiguate homophones, this linguistic information is usually not explicitly incorporated into ASR systems. In this paper, we show that phonetic detail can be used to automatically disambiguate homophones using the example of German pronouns. In these example sentences, “der” fuctions as article (A) and as relative pronoun (B): (A) Hans, der Floh, hatte ein gutes Leben. John,...
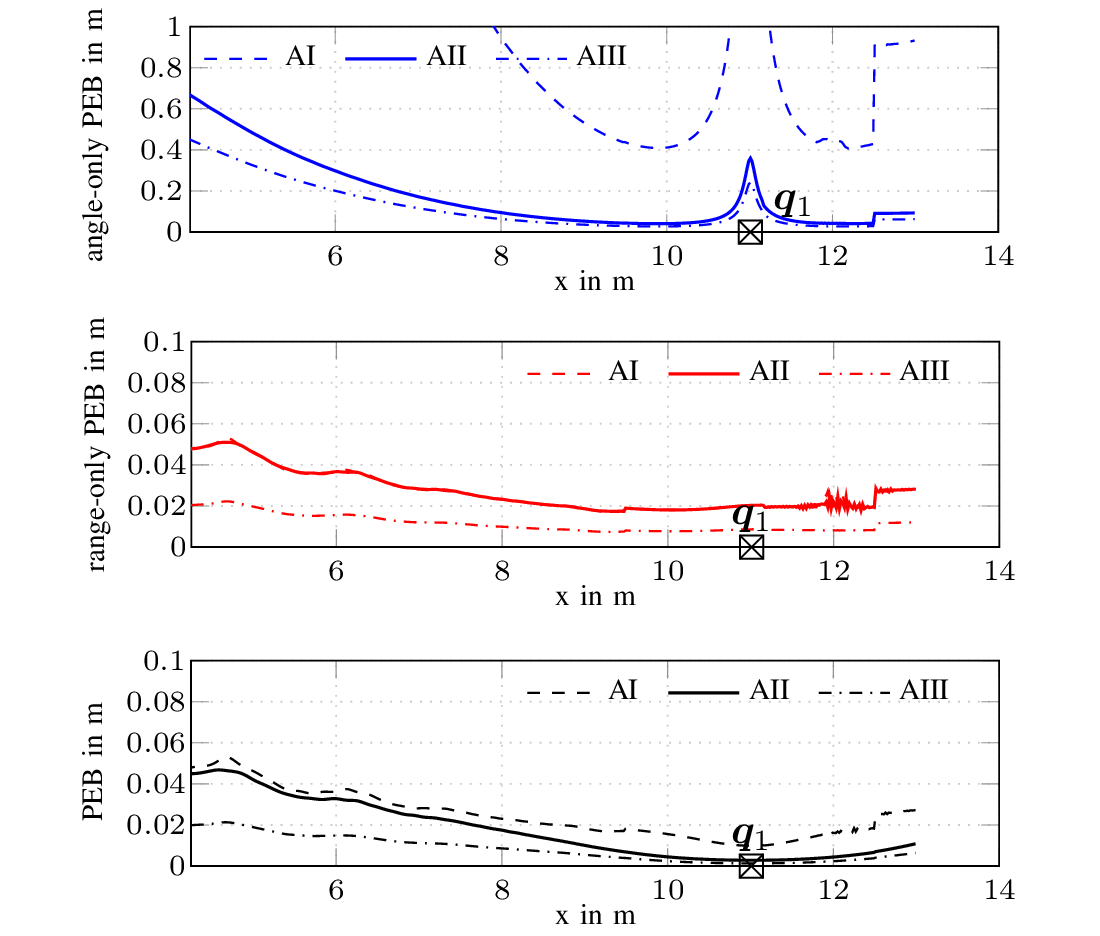
Highly accurate indoor positioning is still a hard problem due to interference caused by multipath propagation and the resulting high complexity of the infrastructure. We focus on the possibility of exploiting information contained in specular multipath components (SMCs) to increase the positioning accuracy of the system and to reduce the required infrastructure, using a-priori information in form of a floor plan. The system utilizes a single anchor equipped with array antennas and wideband signals to allow separating the SMCs. We derive a closed form of the Cramér-Rao lower bound for array-based multipath-assisted positioning and examine the beneficial effect of spatial aliasing of antenna arrays on the achievable angular resolution and as a direct consequence onto the positioning accuracy. It is shown that ambiguities that arise due to the aliasing can be resolved by exploiting the information contained in SMCs. The theoretic results are validated by simulations. The figure illustrates the...
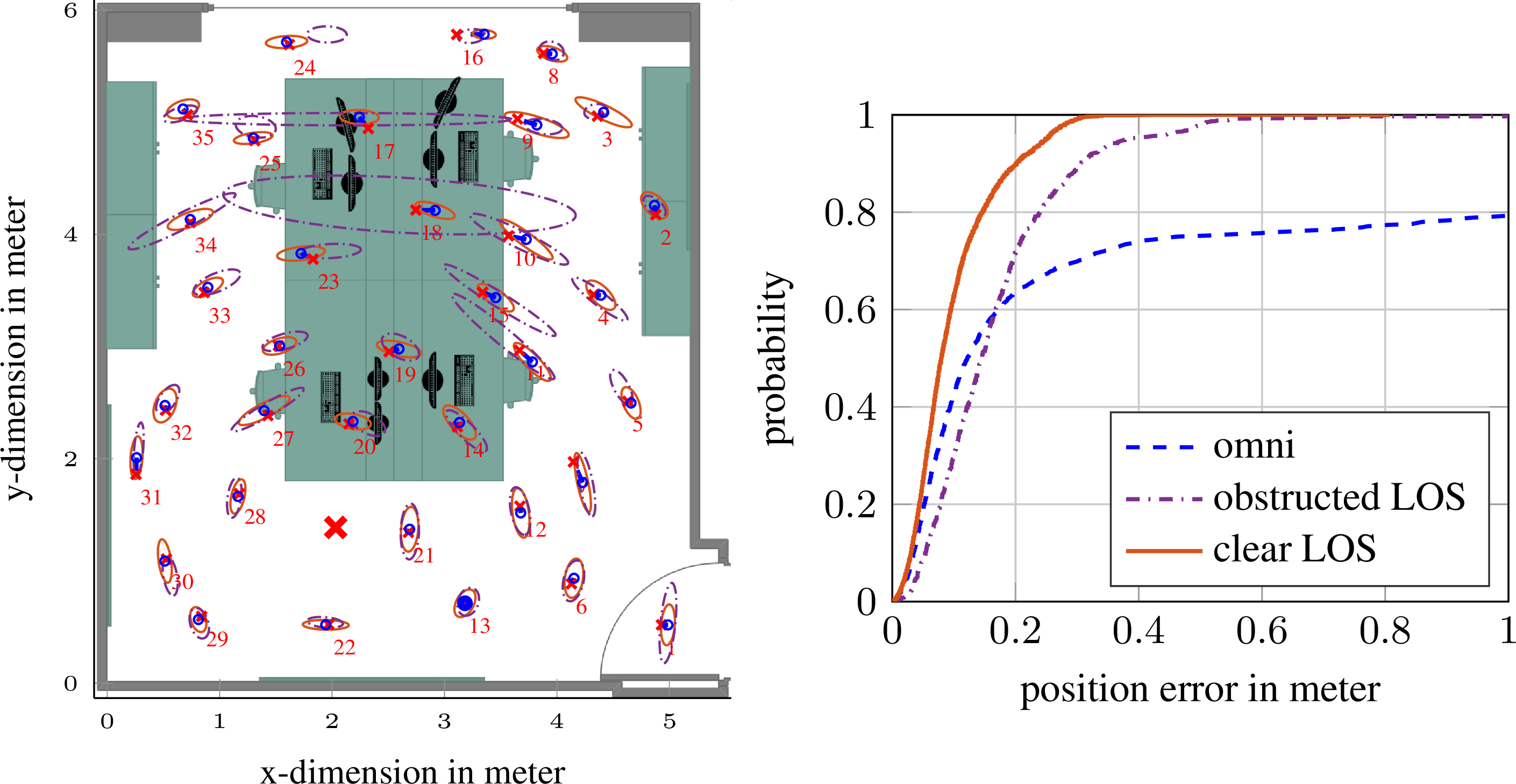
Setting up indoor localization systems is often excessively time-consuming and labor-intensive, because of the high amount of anchors to be carefully deployed or the burdensome collection of fingerprints. In this work, we present SALMA, a novel low-cost ultra-wideband-based indoor localization system that makes use of only one anchor with minimized calibration and training efforts. The system leverages the gained insights of our previous works, exploiting multipath reflections of radio signals to enhance positioning performance. To this end, only a crude floor plan is needed which enables SALMA to accurately determine the position of a mobile tag using a single anchor, hence minimizing the infrastructure costs, as well as the setup time. We implement SALMA on off-the-shelf UWB devices based on the Decawave DW1000 transceiver and show that, by making use of multiple directional antennas, SALMA can also resolve ambiguities due to overlapping multipath components. An experimental evaluation in an office...
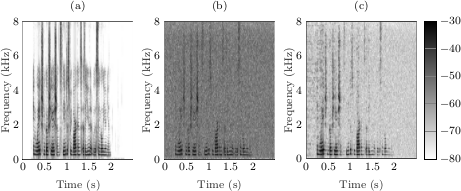
Single-channel speech enhancement refers to the reduction of noise signal components in a single-channel signal composed of both speech and noise. A wide range of single-channel speech enhancement algorithms is formulated in the short-time Fourier transform (STFT). Traditional approaches assume statistical independence between signal components from different time-frequency regions, resulting in estimators that are functions of diagonal covariance matrices. More recent approaches drop this assumption and explicitly model dependencies between STFT bins. Full covariance matrices of speech and noise are required in this case to obtain optimal estimates of the clean speech spectrum, where off-diagonal entries are complex-valued in general. We show that the performance of estimators resulting from such models is highly sensitive to the phase estimation accuracy of these off-diagonal entries. Since it is non-trivial to estimate the covariance phases from noisy speech data, we propose a linear multidimensional short-time spectral amplitude estimator that circumvents the need to...
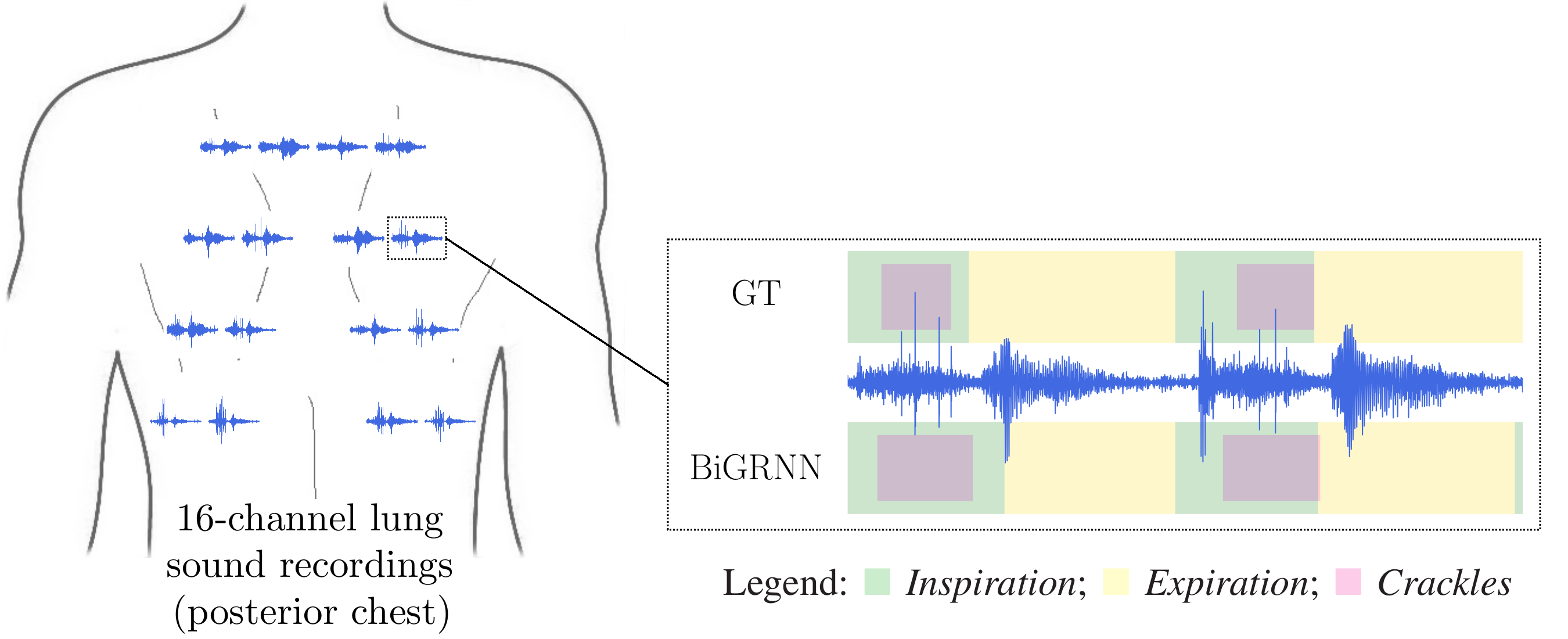
Early diagnosis of idiopathic pulmonary fibrosis (IPF) is of increasing importance, due to recent success to slow down the disease progression. Auscultation is a helpful mean for early diagnosis of IPF. Auscultatory findings for IPF are fine (or velcro) crackles during inspiration, which are heard over affected areas. We present a computer-aided approach for the diagnosis of IPF. In particular, we present a method for event detection in single-channel lung sound recordings. This includes the detection of crackles and breathing phase events (inspiration/ expiration). Therefore, we propose an event detection approach with spectral features and bidirectional gated recurrent neural networks (BiGRNNs). In our experiments, we use multi-channel lung sound recordings from lung-healthy subjects and patients diagnosed with idiopathic pulmonary fibrosis, collected within a clinical trial. We achieve an event-based F-score of F1 ≈86% for breathing phase events and F1 ≈72% for crackles. The proposed method shows robustness regarding the contamination...

One main goal of the recently finished FWF funded project “Cross-layer pronunciation models for conversational speech” was to investigate interdisciplinary approaches towards studying pronunciation variation and to show how researchers in the fields of automatic speech recognition, psycholinguistics and phonetics/phonology can profit from integrating findings of the respective fields. Such new approaches, covering all mentioned disciplines, are presented in the book “Rethinking Reduction”. The book contains 11 peer reviewed chapters, of which two are overview chapters written by the editors, and 9 contain original research. With “Reduction” we refer to acoustically reduced words. In natural conversations, for instance, a word like “yesterday” might be pronounced as yeshay, and a word like “haben” might be pronounced like ham. Phonetically reduced forms are extremely plentiful (e.g., 62% of word tokens in spontaneous Austrian German conversations are reduced), theoretically interesting (e.g., how do people learn to produce and understand the multiple reduced pronunciation...
In this work, we address the problem of estimating the a priori SNR for single-channel speech enhancement. Similar to the decision-directed (DD) approach we linearly combine the maximum likelihood estimate of the current a priori SNR with an estimate obtained from the previous frame. Based on the harmonic model for voiced speech we propose to smooth the a priori SNR estimate along harmonic trajectories instead of fixed discrete Fourier transform frequency bins. We interpolate from fixed DFT frequencies to harmonic frequencies by using a pitch-adaptive zero-padding in the time domain. The resulting pitch-adaptive decision-directed (PADDi) method increases the noise attenuation compared to the classical decision-directed approach and outperforms benchmark methods in terms of speech enhancement performance for several noise types at different SNRs, quantified by objective evaluation criteria. The figure shows spectrograms of clean, noisy, and enhanced speech. The noisy signal is obtained by mixing speech and white noise at...
We present a method to accurately detect the state-sequence first heart sound (S1)–systole–second heart sound (S2)–diastole , i.e., the positions of S1 and S2, in heart sound recordings. We propose an event detection approach without explicitly incorporating a priori information of the state duration. This renders it also applicable to recordings with cardiac arrhythmia and extendable to the detection of extra heart sounds (third and fourth heart sound), heart murmurs, as well as other acoustic events. We use data from the 2016 PhysioNet/CinC Challenge, containing heart sound recordings and annotations of the heart sound states. From the recordings, we extract spectral and envelope features and investigate the performance of different deep recurrent neural network (DRNN) architectures to detect the state sequence. We use virtual adversarial training, dropout, and data augmentation for regularization. We compare our results with the state-of-the-art method and achieve an average score for the four events of...
Recent work has shown substantial performance improvements of discriminative probabilistic models over their generative counterparts. However, since discriminative models do not capture the input distribution of the data, their use in missing data scenarios is limited. To utilize the advantages of both paradigms, we present an approach to train Gaussian mixture models (GMMs) in a hybrid generative-discriminative way. This is accomplished by optimizing an objective that trades off between a generative likelihood term and either a discriminative conditional likelihood term or a large margin term using stochastic optimization. Our model substantially improves the performance of classical maximum likelihood optimized GMMs while at the same time allowing for both a consistent treatment of missing features by marginalization, and the use of additional unlabeled data in a semi-supervised setting. For the covariance matrices, we employ a diagonal plus low-rank matrix structure to model important correlations while keeping the number of parameters small....
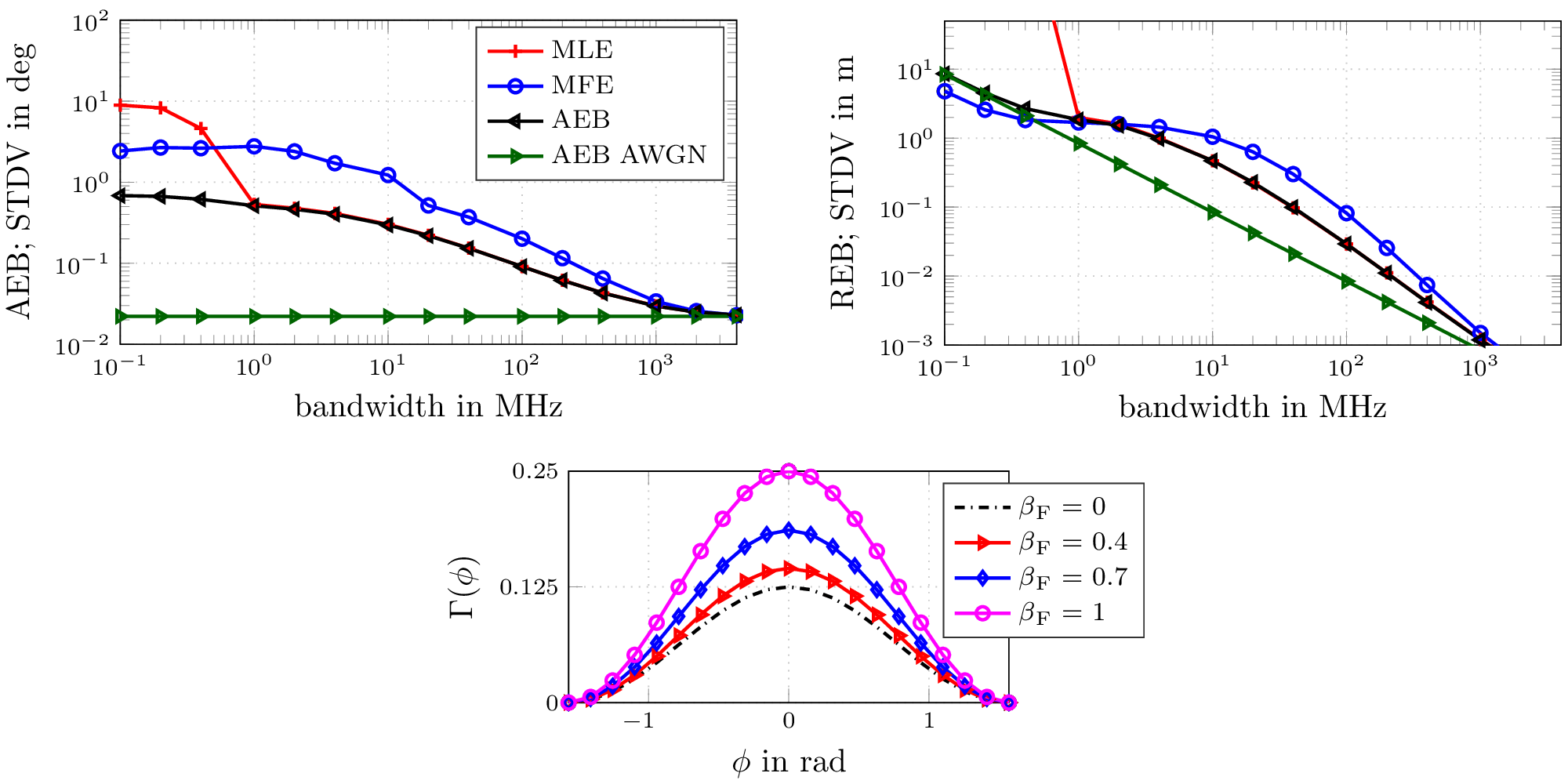
The accuracy that can be achieved in time of arrival (ToA) estimation strongly depends on the utilized signal bandwidth. In an indoor environment multipath propagation usually causes a degradation of the achievable accuracy due to the overlapping signals. A similar effect can be observed for the angle of arrival (AoA) estimation using arrays. This paper derives a closed-form equation for the Cramér-Rao lower bound (CRLB) of the achievable AoA and the ToA error variances, considering the presence of dense multipath. The Fisher information expressions for both parameters allow an evaluation of the influence of channel parameters and system parameters such as the array geometry. Our results demonstrate that the AoA estimation accuracy is strongly related to the signal bandwidth, due to the multipath influence. The theoretical results are evaluated for experimental data, with simulations performed for ULAs with M=2 and M=16 array elements. The figure illustrates the derived ranging error...

Accurate indoor radio positioning requires high-resolution measurements to either utilize or mitigate the impact of multipath propagation. This high resolution can be achieved using large signal-bandwidth, leading to superior time resolution and / or multiple antennas, leading to additional angle resolution. To facilitate multiple antennas, phase-coherent measurements are typically necessary. In this work we propose to employ non-phase-coherent measurements obtained from directional antennas for accurate single-anchor indoor positioning. The derived algorithm exploits beampatterns to jointly estimate multipath amplitudes to be used in maximum likelihood position estimation. Our evaluations based on measured and computer generated data demonstrate only a minor degradation in comparison to a phase-coherent processing scheme. The figure illustrates the likelihood functions, evaluated for a 2D scenario with room size 6x8m. Figures (a) and (b) present the outcome of state-of-the-art algorithms based on phase-coherent (a) and non-phase-coherent measurements (b). The proposed method (c) employs non-phase-coherent measurements and is reaching...

It is intended to achieve similar acoustic conditions as in an already existing live room. The challenges occurring especially in small spaces are introduced and a number of acoustical absorbers are presented. The types of absorbers capable of damping the low frequency room modes are discussed. The acoustic measurements are evaluated, the reverberation time is selected as a significant criterion and a low, frequency-independent target value is chosen. A 3D-model for the acoustic simulation software is built and on the basis of the simulations, various optimisation measures are developed. Concerning an adequate dampening of the room modes, edge or corner absorbers are selected as the basic concept for the enhancement and compound panel absorbers are planned to be installed on the walls. For prevention of flutter echoes and a sufficient gain of absorption and diffusion, a panel system on the ceiling is designed. Finally, the acoustical measures taken are presented...
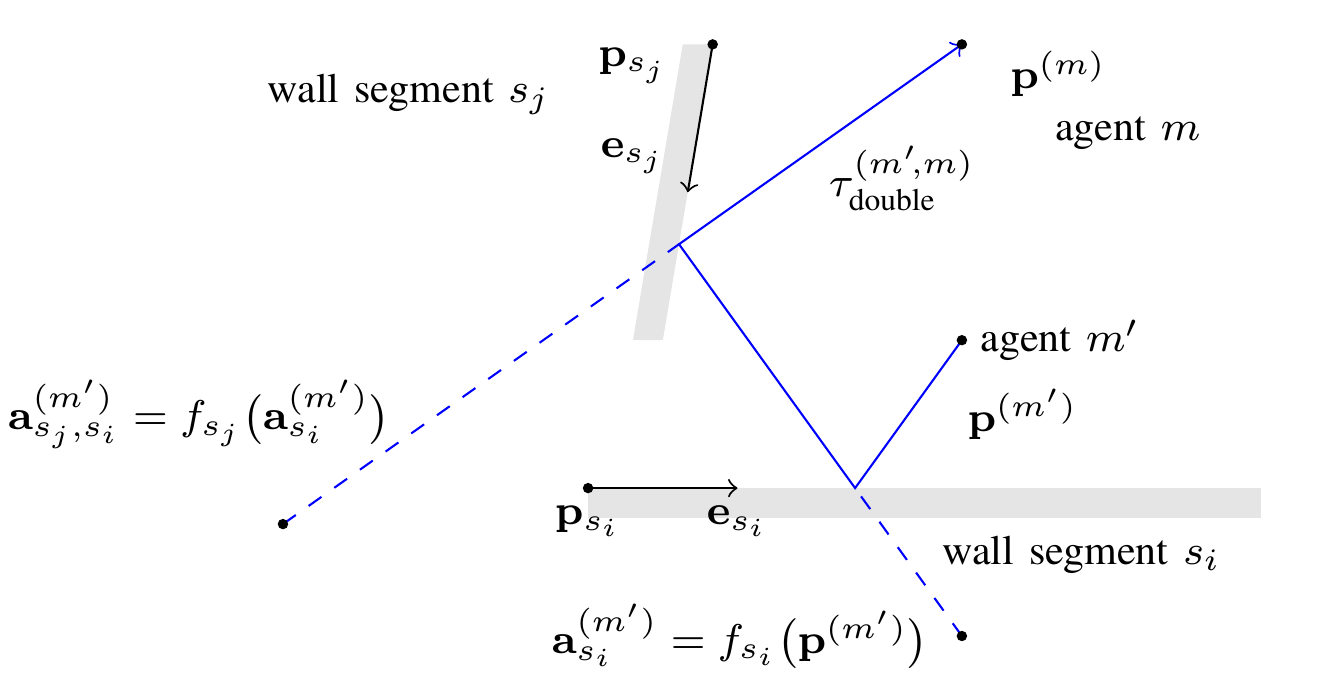
Highly accurate location information is a key facilitator to stimulate future services for the commercial and public sectors. Positioning and tracking of absolute positions of wireless nodes usually requires information provided from technical infrastructure, e.g. satellites or fixed anchor nodes, whose maintenance is costly and whose limited operating coverage narrows the positioning service. In this paper we present an algorithm aiming at tracking of absolute positions without using information from fixed anchors, odometers or inertial measurement units. We perform radio channel measurements in order to exploit position-related information contained in multipath components (MPCs). Tracking of the absolute node positions is enabled by estimation of MPC parameters followed by association of these parameters to a floorplan. To account for uncertainties in the floorplan and for propagation effects like diffraction and penetration, we recursively update the provided floorplan using the measured MPC parameters. We demonstrate the ability to localize two agent nodes...
Speech enhancement methods formulated in the STFT domain vary in the statistical assumptions made on the STFT coefficients, in the optimization criteria applied or in the models of the signal components. Recently, approaches relying on a stochastic-deterministic speech model have been proposed. The deterministic part of the signal corresponds to harmonically related sinusoids, often used to represent voiced speech. The stochastic part models signal components that are not captured by the deterministic components. In this work, we consider this scenario under a new perspective yielding three main contributions. First, a pitch-synchronous signal representation is considered and shown to be advantageous for the estimation of the harmonic model parameters. Second, we model the harmonic amplitudes in voiced speech as random variables with frequency bin dependent Gamma distributions. Finally, distinct estimators for the different models of voiced speech, unvoiced speech, and speech absence are derived. To select from the arising estimates, we...
The IMS student design competitions are an annual event at the IEEE MTT-S International Microwave Symposium. In 2017, the SPSC lab members Harald Enzinger and Karl Freiberger won the first prize in the competition “Power Amplifier Linearization through Digital Predistortion”. The aim of this competition was to linearize a highly efficient but nonlinear envelope tracking power amplifier in dual-band operation by means of digital predistortion. The winning solution combines several state-of-the-art methods for crest factor reduction (CFR) and digital predistortion (DPD) with new extensions, developed specifically for this competition. You can find out more about this winning solution in the Jannuary/February issue of the IEEE Microwave Magazine. A preprint version of the paper can be downloaded from the SPSC website. The image shows the amplitude modulation to amplitude modulation (AM-AM) and amplitude modulation to phase modulation (AM-PM) characteristics of one frequency band before and after linearization. The dispersion due to...
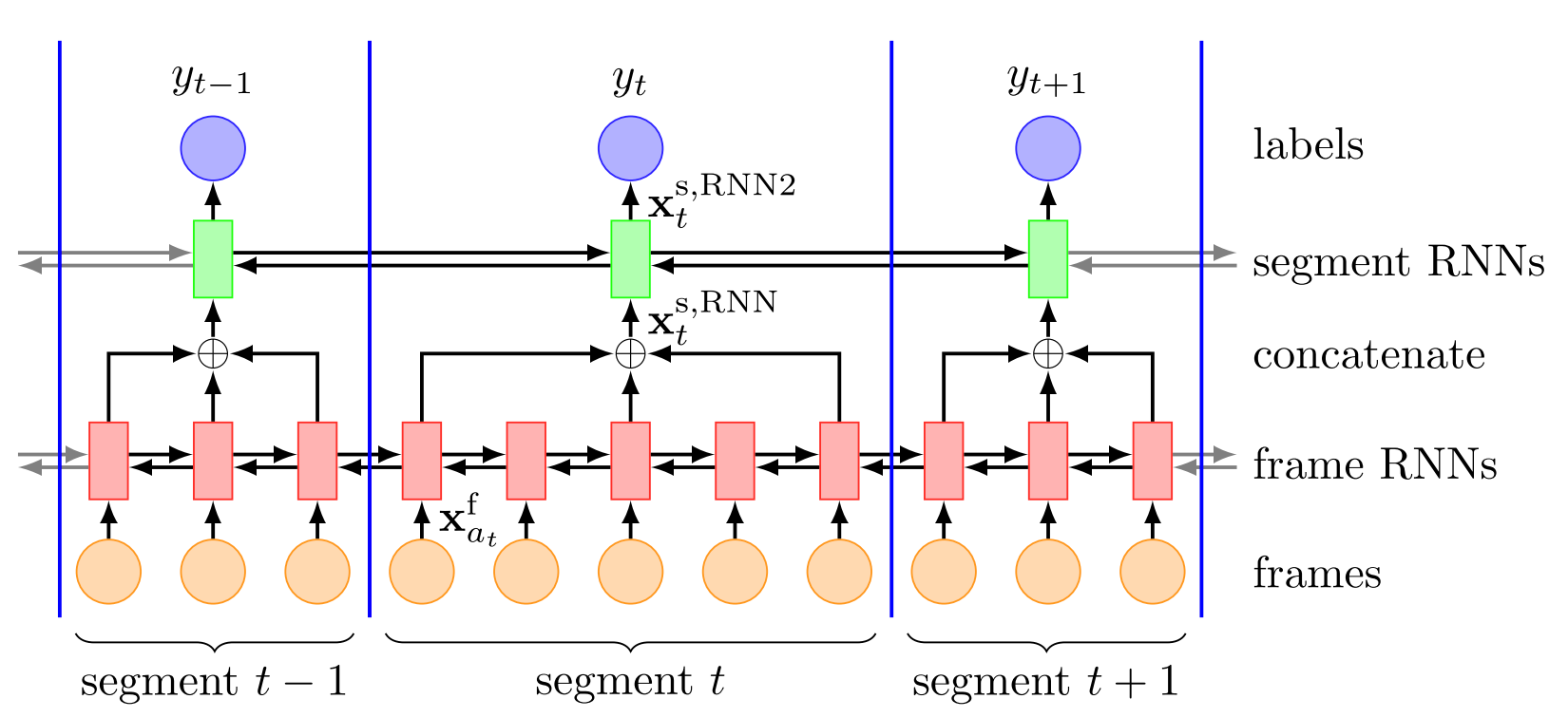
We introduce a simple and efficient frame and segment level RNN model (FS-RNN) for phone classification. It processes the input at frame level and segment level by bidirectional gated RNNs. This type of processing is important to exploit the (temporal) information more effectively compared to (i) models which solely process the input at frame level and (ii) models which process the input on segment level using features obtained by heuristic aggregation of frame level features. Furthermore, we incorporated the activations of the last hidden layer of the FS-RNN as an additional feature type in a neural higher-order CRF (NHO-CRF). In experiments, we demonstrated excellent performance on the TIMIT phone classification task, reporting a performance of 13.8% phone error rate for the FS- RNN model and 11.9% when combined with the NHO-CRF. In both cases we significantly exceeded the state-of-the-art performance. We gave an oral presentation of this work at Interspeech...
We consider a lossy single-user caching problem with correlated sources – just think of streaming compressed videos! Most users will watch these videos in the evening, leading to network congestion. If you have a player with a cache, though, you can fill this cache with data during times of low network usage, even though you may not know which video the user wants to watch in the evening. In our paper, we characterize the transmission rate required in the evening as a function of the cache size and as a function of the distortion one accepts when watching the videos. We furthermore hint at what should be put in the cache such that it is useful for a variety of videos, and we connect these results to the common-information measures proposed by Wyner, Gacs and Koerner. The picture shows achievable upper (red) and lower converse (black) bounds on the transmission...
In this work, we obtain all fixed points of belief propagation and perform a local stability analysis. We consider pairwise interactions of binary random variables and investigate the influence of non-vanishing fields and finite-size graphs on the performance of belief propagation; local stability is heavily influenced by these properties. We show why non-vanishing fields help to achieve convergence and increase the accuracy of belief propagation. We further explain the close connections between the underlying graph structure, the existence of multiple solutions, and the capability of belief propagation (with damping) to converge. Finally, we provide insights into why finite-size graphs behave better than infinite-size graphs. The figures show all stationary points of belief propagation for grid graphs and fully connected graphs. The exact solution is depicted in red and approximate solutions are shown in blue (stable), black (stable with damping), and green (unstable). More information can be found in our paper....
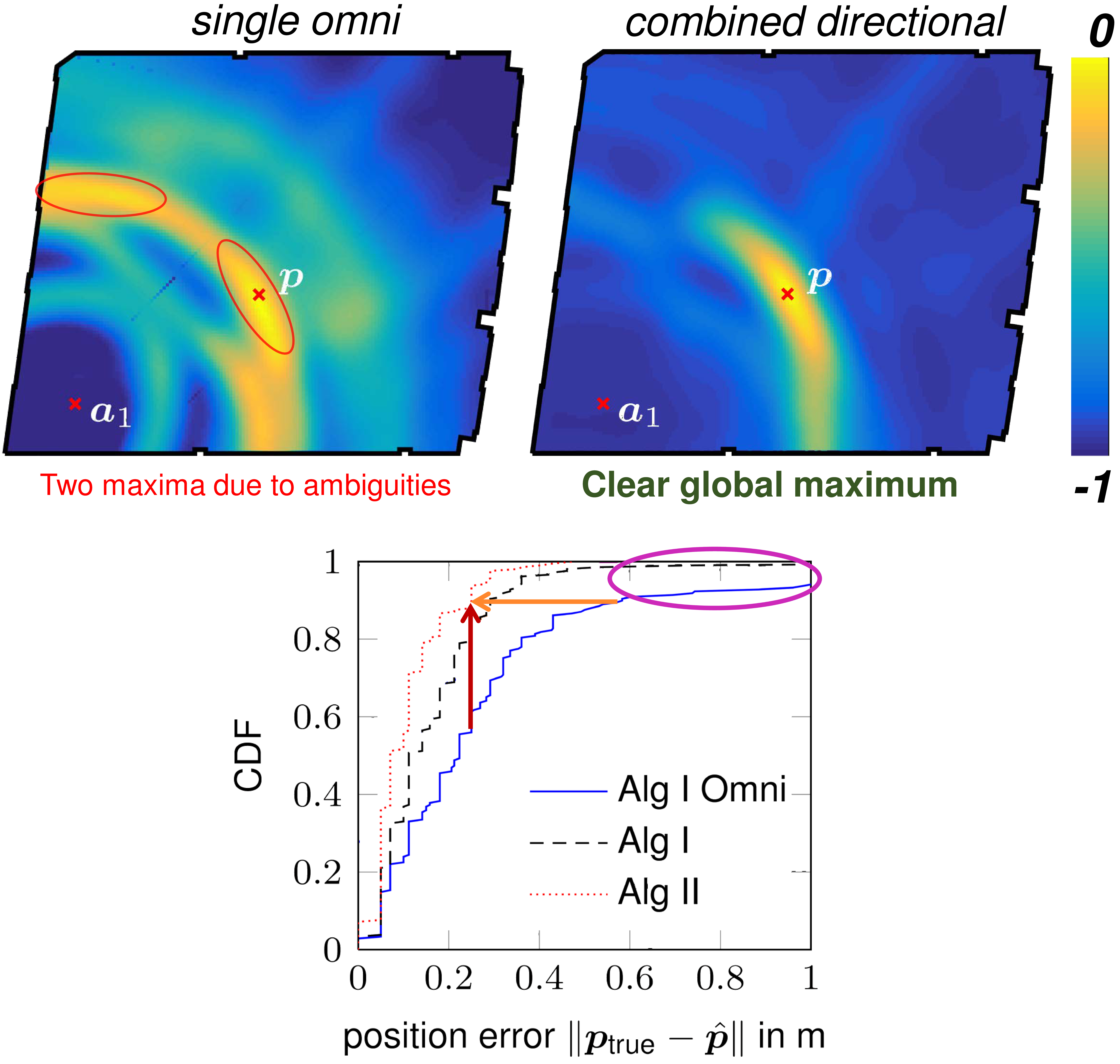
High-accuracy indoor radio positioning can be achieved by using high signal bandwidths to increase the time resolution. Multiple fixed anchor nodes are needed to compute the position or alternatively, reflected multipath components can be exploited with a single anchor. In this work, we propose a method that explores the time and angular domains with a single anchor. This is enabled by switching between multiple directional ultra-wideband (UWB) antennas. The UWB transmission allows to perform multipath resolved indoor positioning, while the directionality increases the robustness to undesired, interfering multipath propagation with the benefit that the required bandwidth is reduced. The positioning accuracy and performance bounds of the switched antenna are compared to an omni-directional antenna. Two positioning algorithms are presented based on different prior knowledge available, one using floorplan information only and the other using additionally the beampatterns of the antennas. We show that the accuracy of the position estimate is...
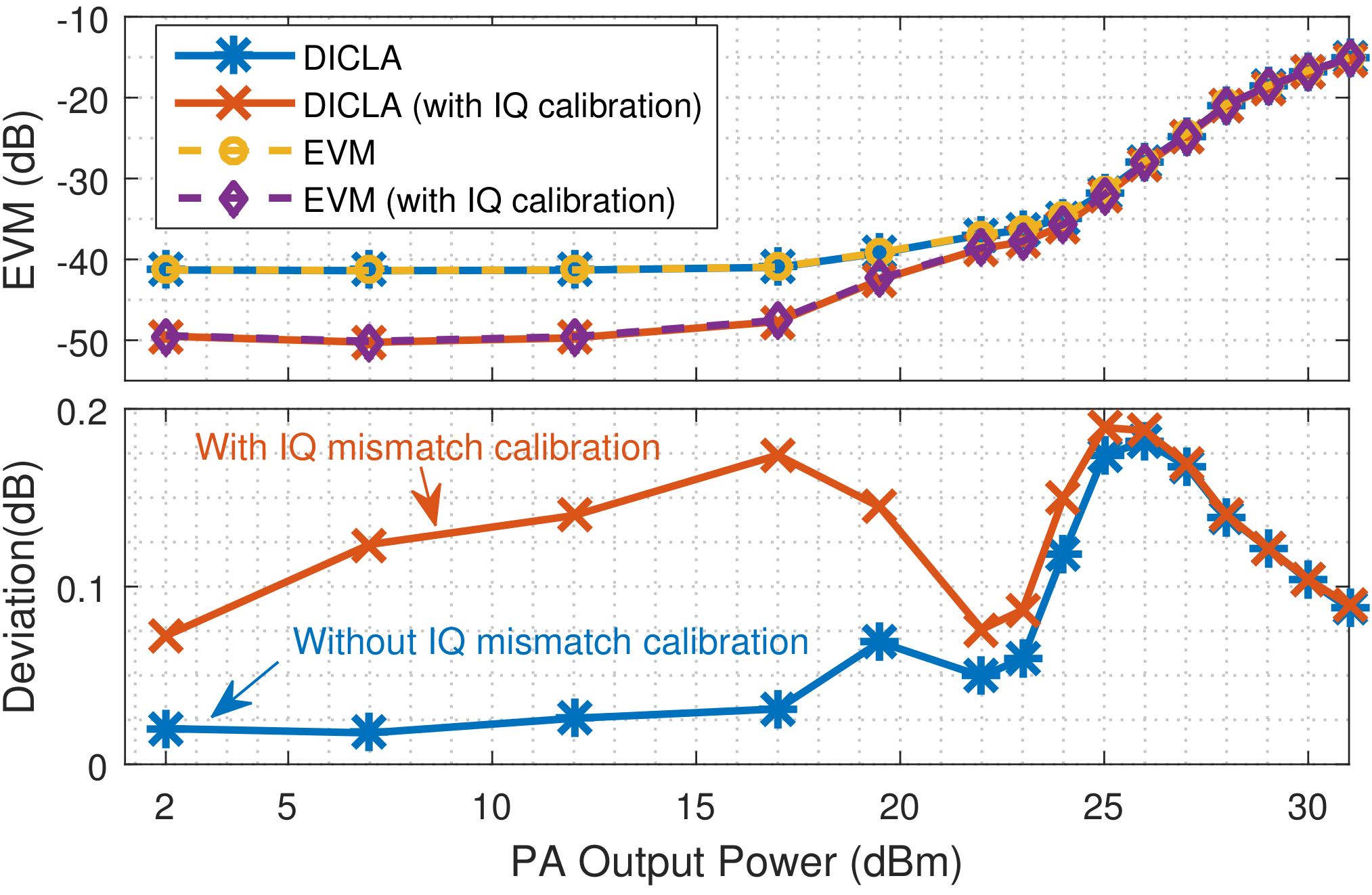
We present a method for measuring a communication signal’s inband error caused by a non-ideal device under test (DUT). In contrast to the established error vector magnitude (EVM), we do not demodulate the data symbols. Rather, we subtract linearly correlated (SLIC) parts from the DUT output and analyze the power spectral density of the remaining error signal. Consequently, we do not require in-depth knowledge of the modulation standard. This makes our method well suited for measurements with cutting-edge communication signals, without the need to purchase or implement a dedicated EVM analyzer. We show that our SLIC-EVM approach allows for estimating the subcarrier-dependent EVM for typical transceiver impairments like IQ mismatch, phase noise, and power amplifier (PA) nonlinearity. We present measurement results of a WLAN PA, showing less than 0.2 dB absolute deviation from the regular EVM with demodulation. The figure presents measurement results of the RFMD RFPA5522 power amplifier using...
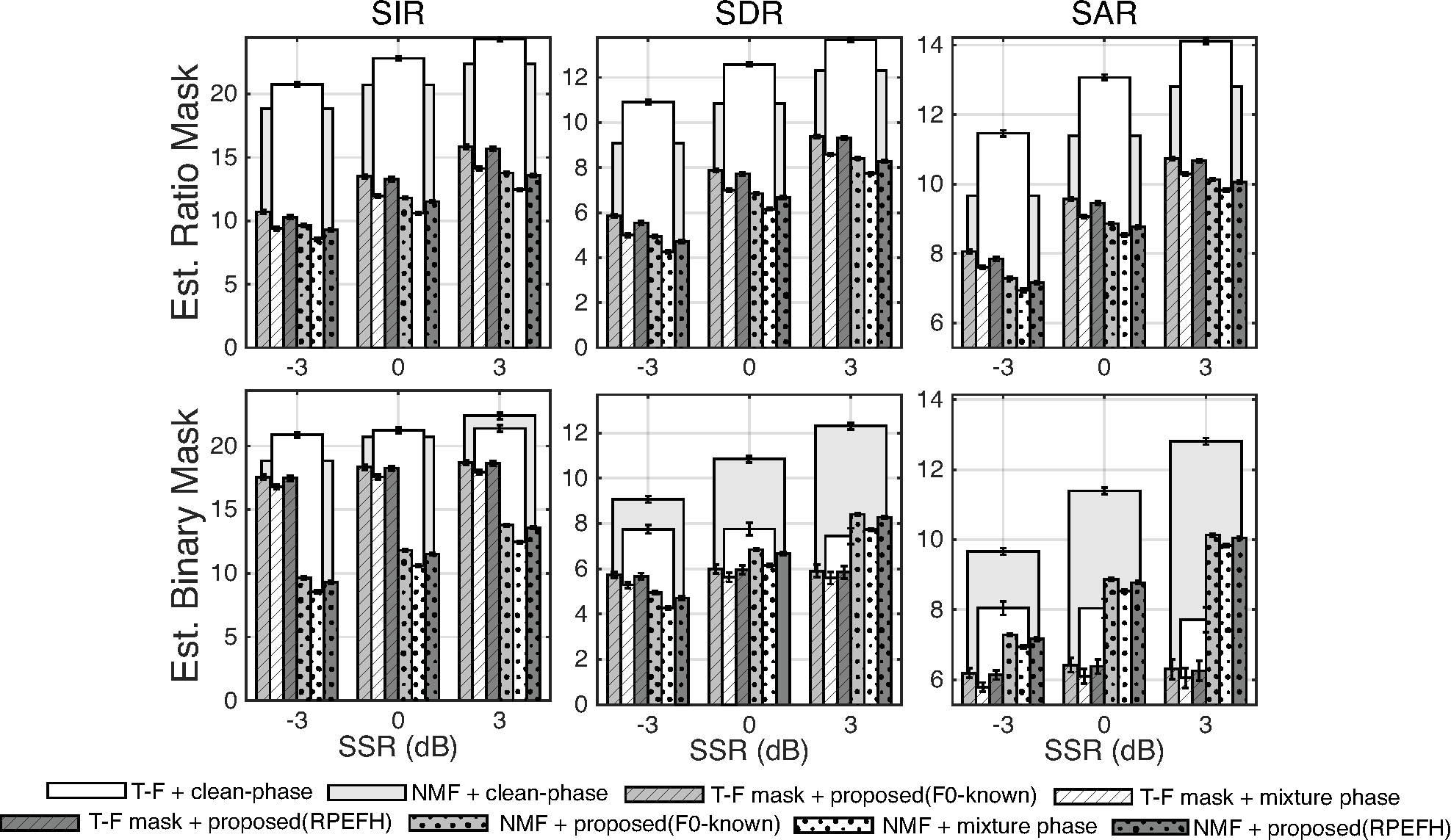
Time-frequency masking is a common solution for the single-channel source separation (SCSS) problem where the goal is to find a time-frequency mask that separates the underlying sources from an observed mixture. An estimated mask is then applied to the mixed signal to extract the desired signal. During signal reconstruction, the time-frequency–masked spectral amplitude is combined with the mixture phase. This article considers the impact of replacing the mixture spectral phase with an estimated clean spectral phase combined with the estimated magnitude spectrum using a conventional model-based approach. As the proposed phase estimator requires estimated fundamental frequency of the underlying signal from the mixture, a robust pitch estimator is proposed. The upper-bound clean phase results show the potential of phase-aware processing in single-channel source separation. Also, the experiments demonstrate that replacing the mixture phase with the estimated clean spectral phase consistently improves perceptual speech quality, predicted speech intelligibility, and source separation...
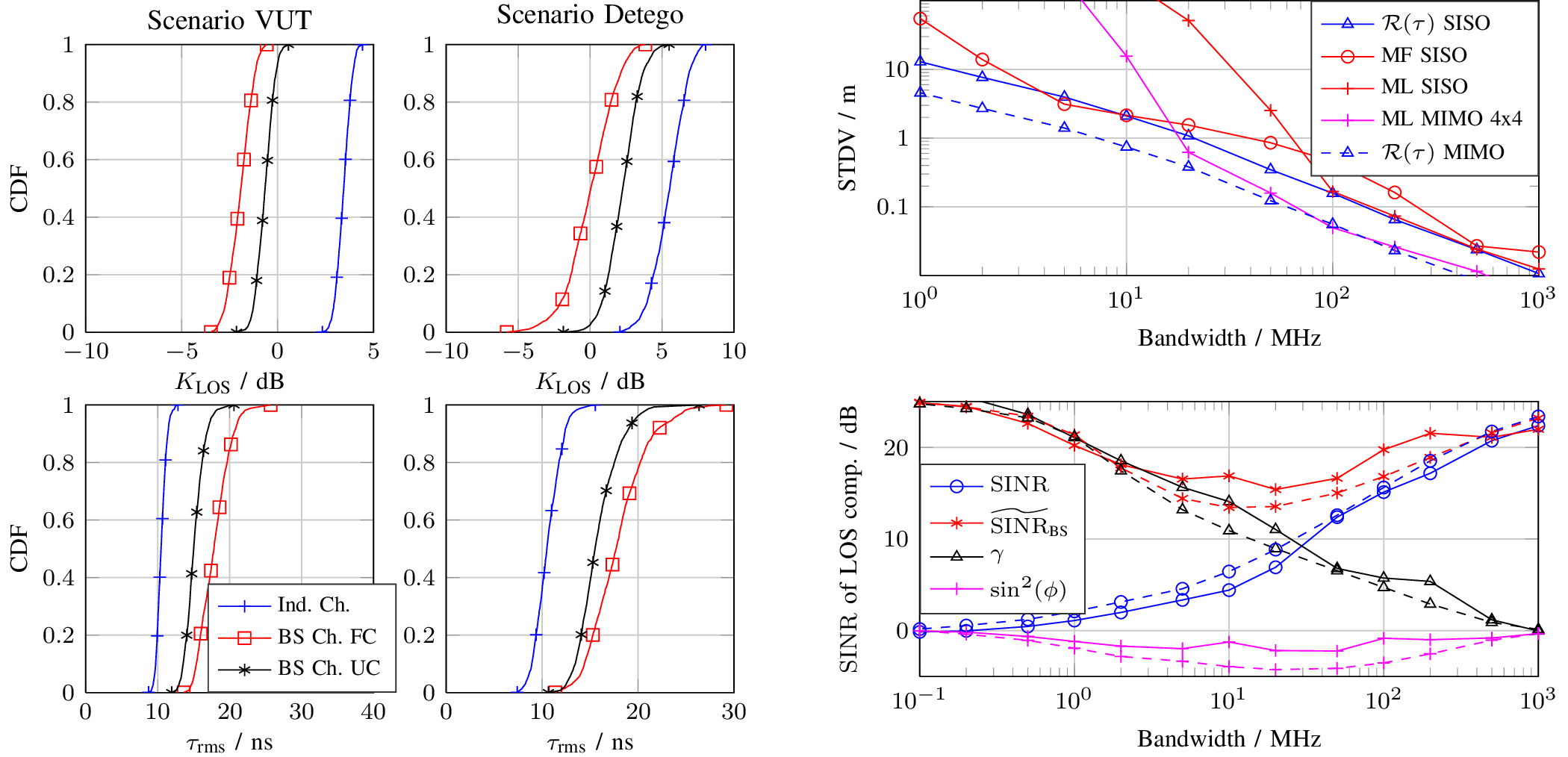
Positioning and ranging within UHF RFID are highly dependent on the channel characteristics. The accuracy of time-of-flight based ranging systems is fundamentally limited by the available bandwidth. We thus analyze the UHF RFID backscatter channel formed by convolution of the individual constituent channels. For this purpose, we present comprehensive wideband channel measurements in two representative scenarios and an analysis with respect to the Rician K-factor for the line-of-sight component, the root-mean-square delay spread, and the coherence distance, which all influence the potential positioning performance. On the basis of these measurements, we validate the Cramer Rao lower bound for time-of-flight based ranging under the influence of dense multipath and present two types of range estimators, a maximum likelihood and a matched filter approach. The resulting range estimates highlight the need for an increased bandwidth for UHF RFID systems with respect to time-of-flight based ranging. The left hand side of the figure...
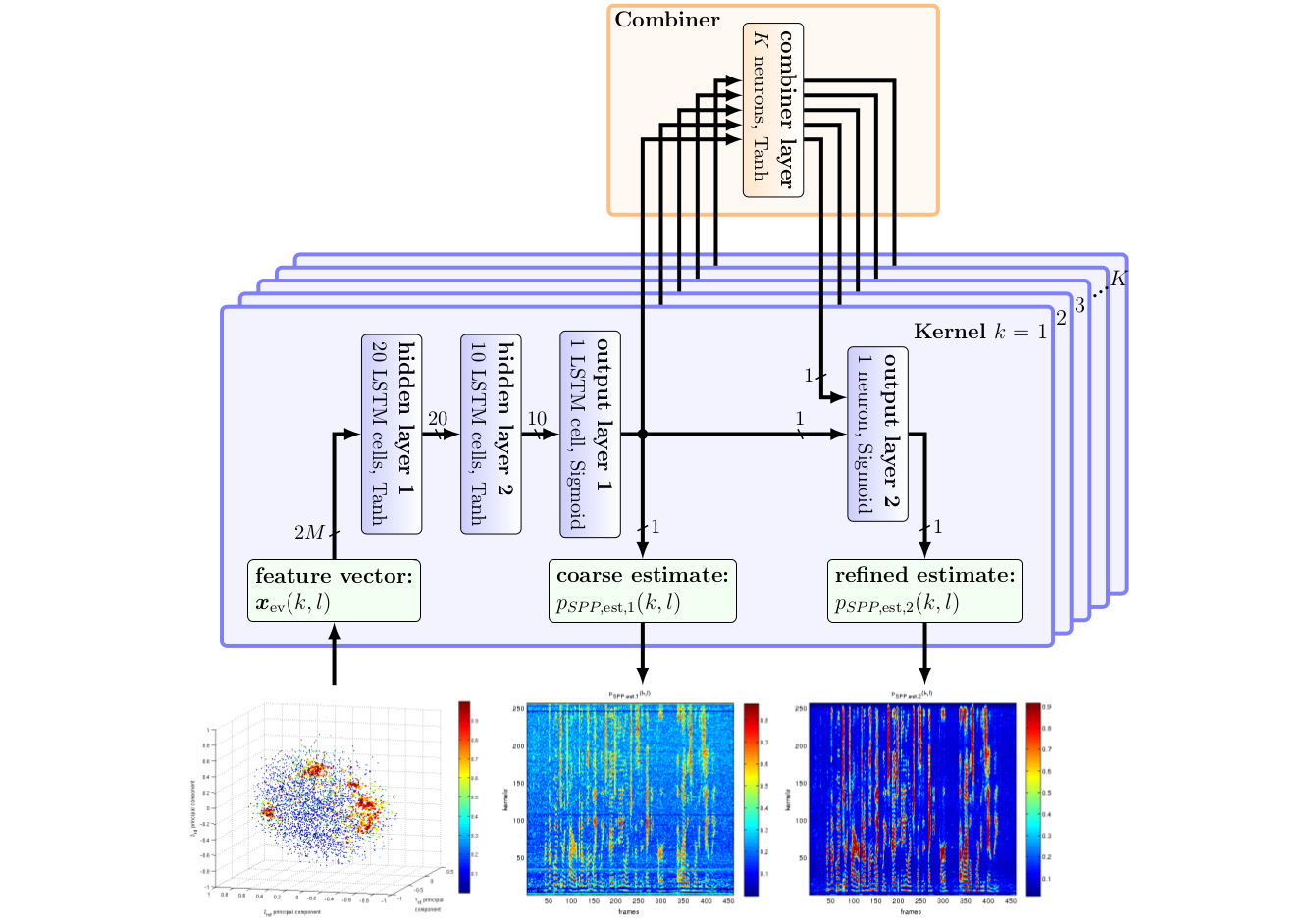
Using speech masks for multi-channel speech enhancement gained attention over the last years, as it combines the benefits of digital signal processing (beamforming) and machine-learning (learn the speech mask from data). We demonstrate how a speech mask can be used to construct the Minimum Variance Distortionless response (MVDR), Generalized Sidelobe Canceler (GSC) and Generalized Eigenvalue (GEV) beamformers, and a MSE-optimal postfilter. We propose a neural network architecture that learns the speech mask from the spatial information hidden in the multi-channel input data, by using the dominant eigenvector of the Power Spectral Density (PSD) matrix of the noisy speech signal as feature vector. We use CHiME-4 audio data to train our network, which contains a single speaker engulfed in ambient noise. Depending on the speakers location and the geometry of the microphone array the eigenvectors form local clusters, whereas they are randomly distributed for the ambient noise. The neural network learns...
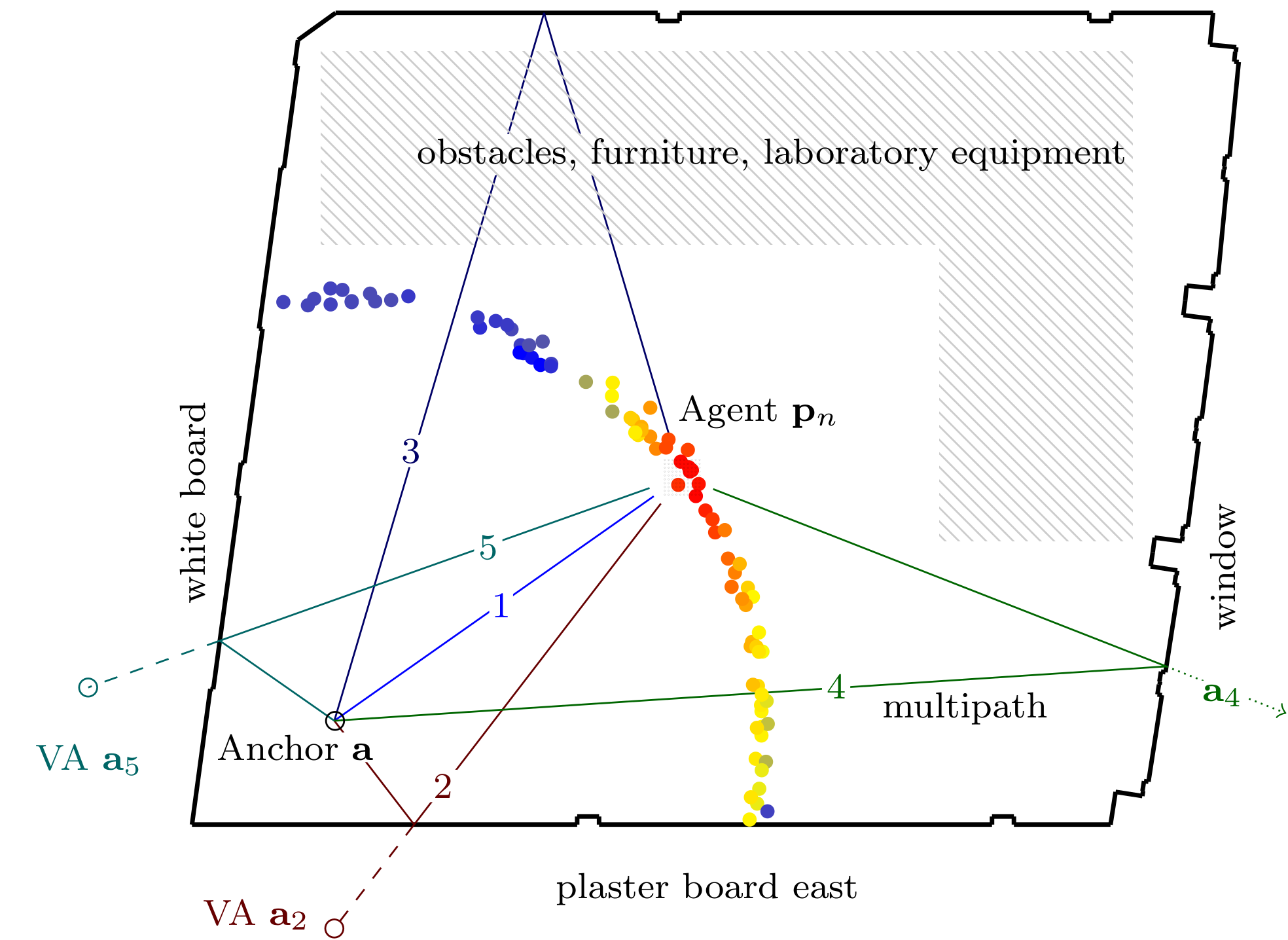
Robust indoor positioning at sub-meter accuracy typically requires highly accurate radio channel measurements to extract precise time-of-flight measurements. Emerging UWB transponders like the DecaWave DW1000 chip offer to estimate channel impulse responses with a reasonably high bandwidth, yielding a ranging precision below 10 cm. The competitive pricing of these chips allows scientists and engineers for the first time to exploit the benefits of UWB for indoor positioning without the need for a massive investment into experimental equipment. The figure illustrates the employment of multipaths (numbers 1-5) to estimate the agent’s position using a single channel-impulse-response measurement only. The colored dots represent the evaluated likelihood where brighter indicates a better model fit regarding the observation. More information can be found in the paper and here.
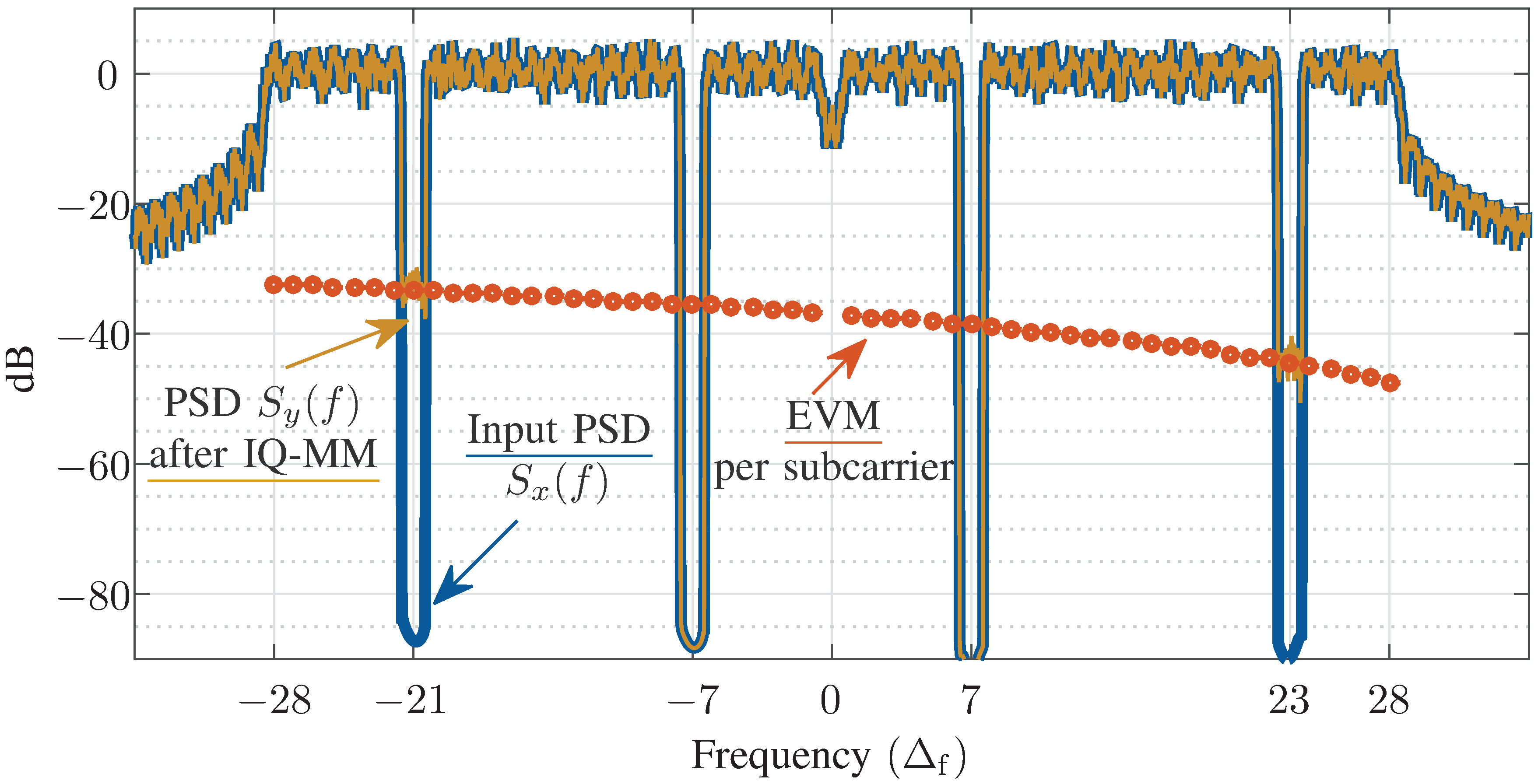
Error vector magnitude (EVM) and noise power ratio (NPR) measurements are well-known approaches to quantify the inband performance of communication systems and their respective components. In contrast to NPR, EVM is an important design specification and is widely adopted by modern communication standards such as 802.11 (WLAN). However, EVM requires full demodulation, whereas NPR excels with simplicity requiring only power measurements in different frequency bands. Consequently, NPR measurements avoid bias due to insufficient synchronization and can be readily adapted to different standards and bandwidths. We argue that NPR-inspired measurements can replace EVM in many practically relevant cases. We show how to set up the signal generation and analysis for power-ratio-based estimation of EVM in orthogonal frequency-division multiplexing systems impaired by additive noise, power amplifier nonlinearity, phase noise, and in-phase–quadrature (IQ) imbalance. Our method samples frequency-dependent inband errors via a single measurement and can either include or exclude the effect of...
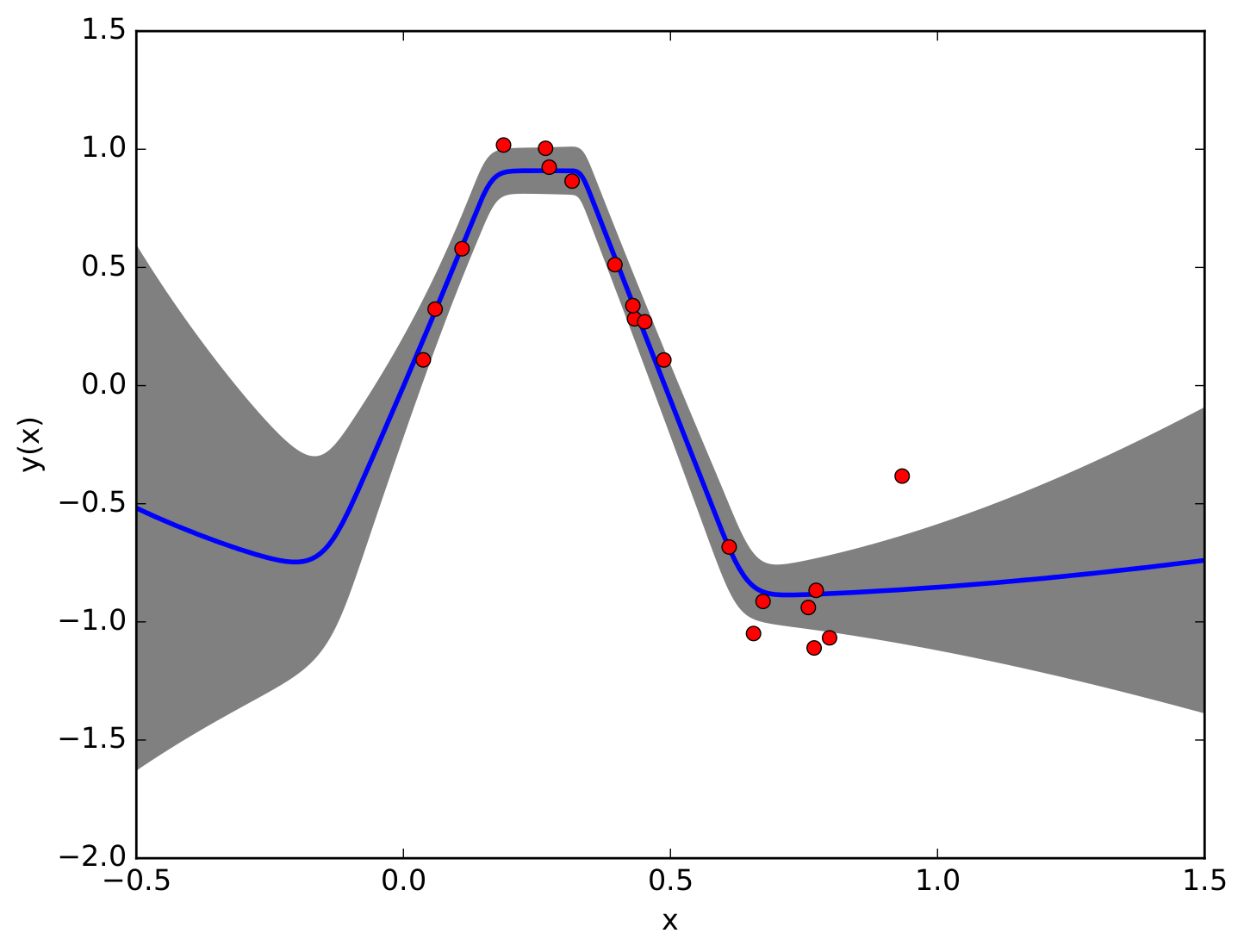
We propose a closed-form approximation of the intractable KL divergence objective for variational inference in neural networks. The approximation is based on a probabilistic forward pass where we successively propagate probabilities through the network. Unlike existing variational inferences schemes that typically rely on stochastic gradients that often suffer from high variance our method has a closed-form gradient. Furthermore, the probabilistic forward pass inherently computes expected predictions together with uncertainty estimates at the outputs. In experiments, we show that our model improves the performance of plain feed-forward neural networks. Moreover, we show that our closed-form approximation works well compared to model averaging and that our model is capable of producing reasonable uncertainties in regions where no data is observed. Figure: Common neural networks simply compute a point-estimate y(x) for a given input x (blue line). Our model additionally produces uncertainties that show how confident the model is about its prediction (shaded region). The uncertainties are larger in regions where no data is observed. For more information,...
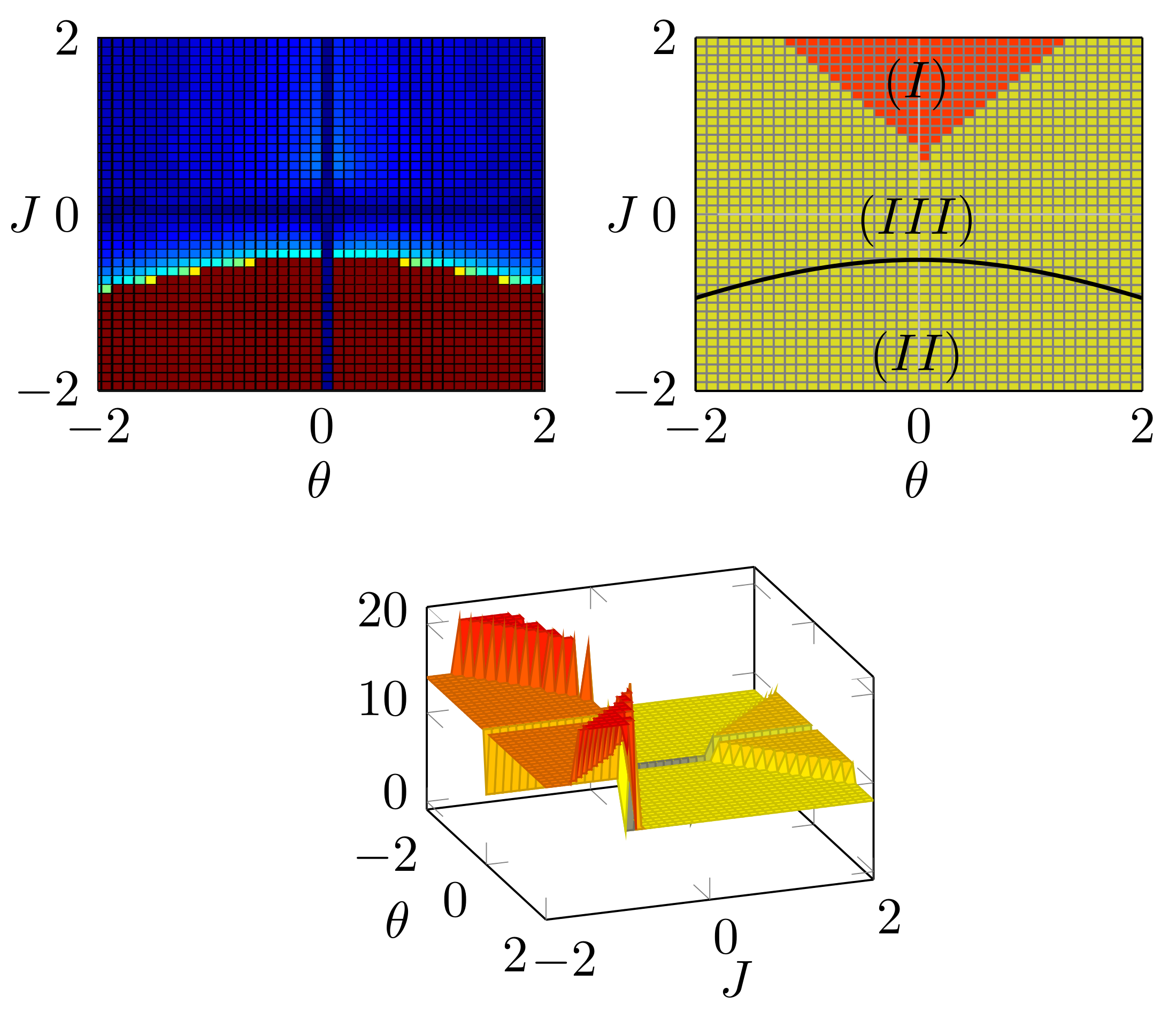
Belief propagation is an iterative method to perform approximate inference on arbitrary graphical models. Whether it converges and if the solution is a unique fixed point depends on both, the structure and the parametrization of the model. To understand this dependence it is interesting to find all fixed points. We formulate a set of polynomial equations, the solutions of which correspond to BP fixed points. Experiments on binary Ising models show how our method is capable of obtaining all fixed points. The figure on the upper-left-hand-side shows the number of iterations until belief propagation converged – for red it did not converge at all. The upper-right-hand-figure shows the number of fixed points (yellow: unique fixed point, red: three fixed points). Phase transitions separate the parameter space into three distinct regions. In the lower figure the number of real solutions is depicted: at the onset of phase transitions a sudden increase...
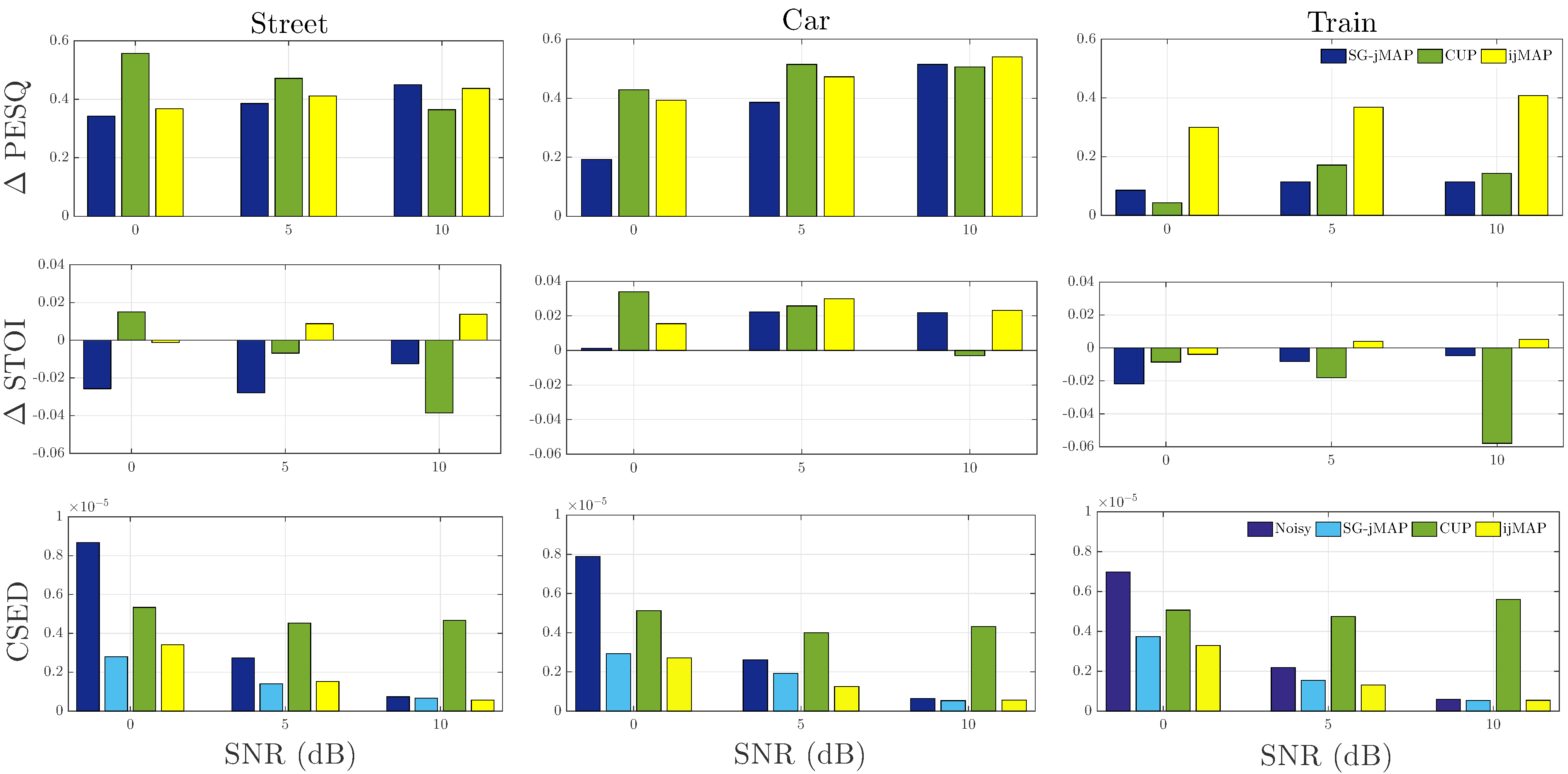
Within the last three decades research in single-channel speech enhancement has been mainly focused on filtering the noisy spectral amplitude without that much focus on the integration of phase-based signal processing. Recently, several phase-aware algorithms based on phase-sensitive signal models were proposed for speech enhancement using the minimum mean squared error (MMSE). Improved performance over the conventional phase-insensitive approaches has been achieved. In this paper, we propose an iterative joint maximum a posteriori (MAP) amplitude and phase estimator (ijMAP) assuming a non-uniform phase distribution. Experimental results demonstrate the effectiveness of the proposed method in recovering both amplitude and phase in noise, justified by perceived quality, speech intelligibility and phase estimation error instrumental measures. The proposed method, brings joint improvement in perceived quality and speech intelligibility compared to the phase-blind joint MAP estimator with a comparable performance to the complex MMSE estimator. The figure shows barplots evaluating the speech enhancement performance...

An overview on the challenging new topic of phase-aware signal processing Speech communication technology is a key factor in human-machine interaction, digital hearing aids, mobile telephony, and automatic speech/speaker recognition. With the proliferation of these applications, there is a growing requirement for advanced methodologies that can push the limits of the conventional solutions relying on processing the signal magnitude spectrum. Single-Channel Phase-Aware Signal Processing in Speech Communication provides a comprehensive guide to phase signal processing and reviews the history of phase importance in the literature, basic problems in phase processing, fundamentals of phase estimation together with several applications to demonstrate the usefulness of phase processing. Key features: Analysis of recent advances demonstrating the positive impact of phase-based processing in pushing the limits of conventional methods. Offers unique coverage of the historical context, fundamentals of phase processing and provides several examples in speech communication Provides a detailed review of many references...
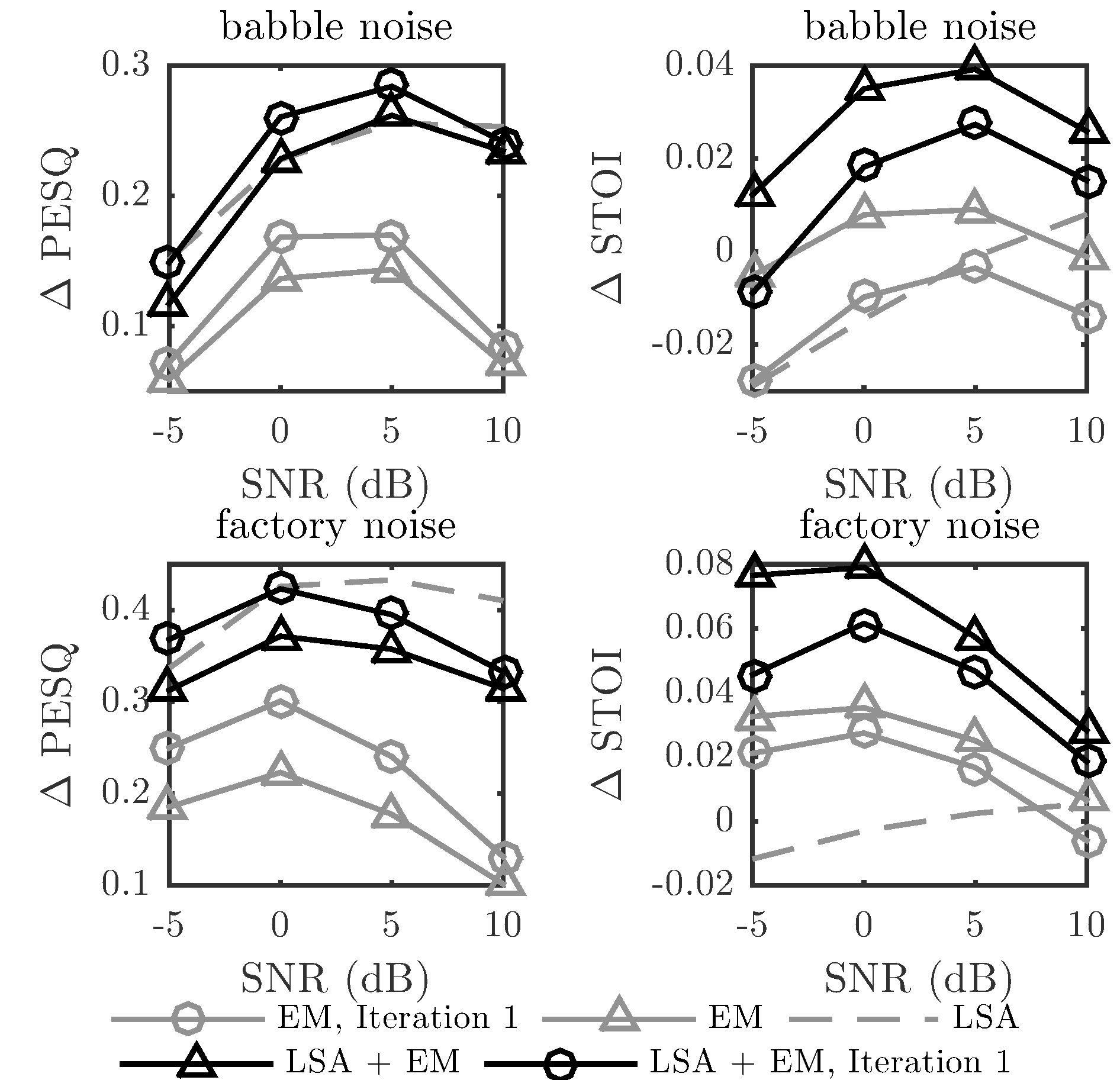
In digital speech transmission the transmitted speech signal is often corrupted by noise arising from various kinds of sources such as passing cars or chatting people in a restaurant. The aim of speech enhancement is to compensate for the detrimental effects these interferences have on the speech quality. In this work we present a method to enhance voiced speech segments only, which are often modeled as a sum of harmonically related sinusoids. We propose an iterative estimation scheme to jointly estimate the harmonic parameters, i.e., amplitude, frequency and phase of the harmonics of the underlying speech signal. Here we utilize the expectation-maximazation (EM) algorithm to obtain the harmonic parameters which are then used to reconstruct voiced speech segments. The potential of the proposed speech enhancement method in terms of harmonic parameter estimation is validated on synthetic harmonic signals. Further, by applying it to noise corrupted speech files we demonstrate its...
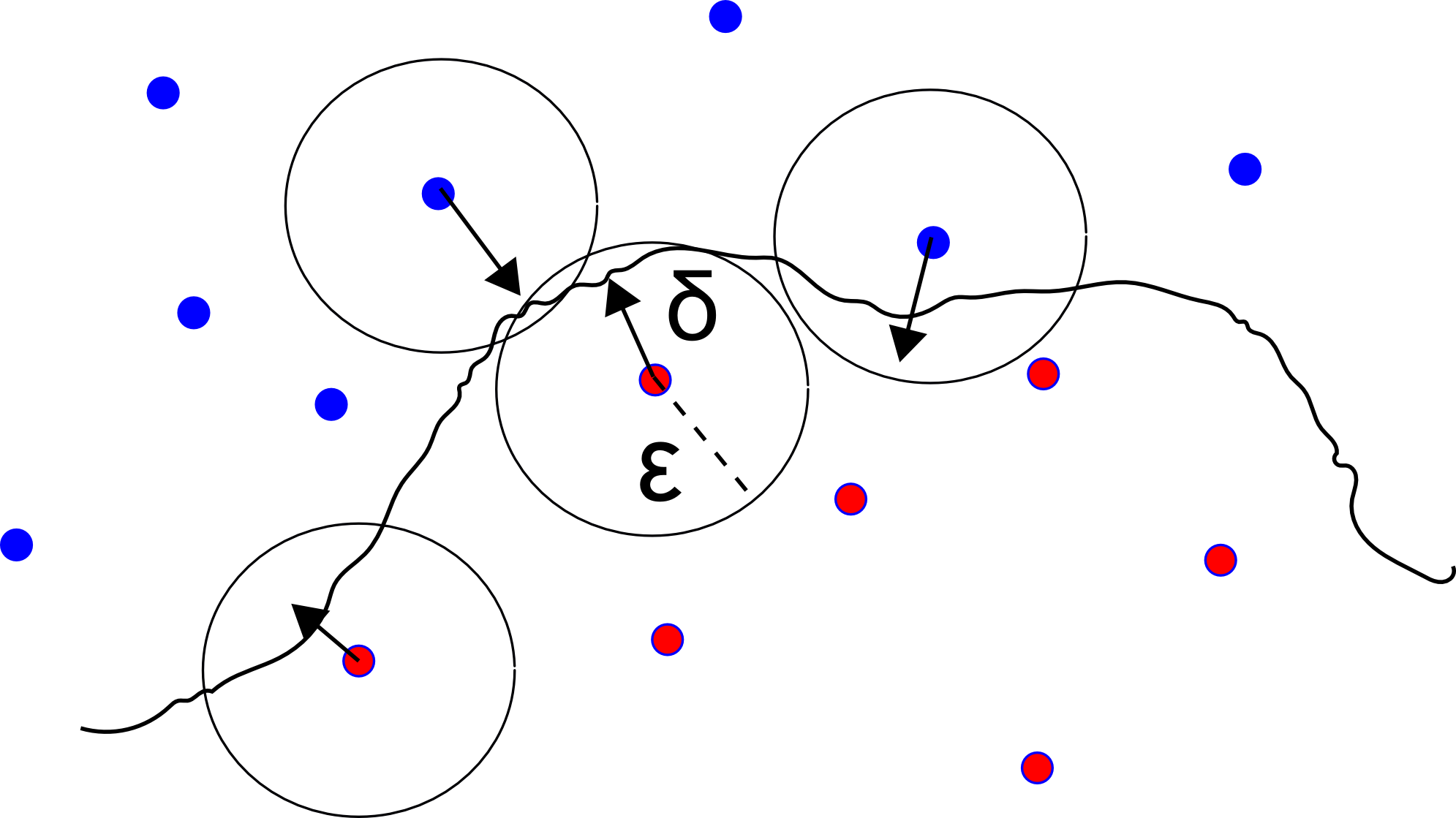
We explore virtual adversarial training (VAT) applied to neural higher-order conditional random fields for sequence labeling. VAT is a recently introduced regularization method promoting local distributional smoothness: It counteracts the problem that predictions of many state-of-the-art classifiers are unstable to adversarial perturbations. Unlike random noise, adversarial perturbations are minimal and bounded perturbations that flip the predicted label. We utilize VAT to regularize neural higher-order factors in conditional random fields. These factors are for example important for phone classification where phone representations strongly depend on the context phones. However, without using VAT for regularization, the use of such factors was limited as they were prone to overfitting. In extensive experiments, we successfully apply VAT to improve performance on the TIMIT phone classification task. In particular, we achieve a phone error rate of 13.0%, exceeding the state-ofthe-art performance by a wide margin. We will give an oral presentation at Interspeech 2016. More...
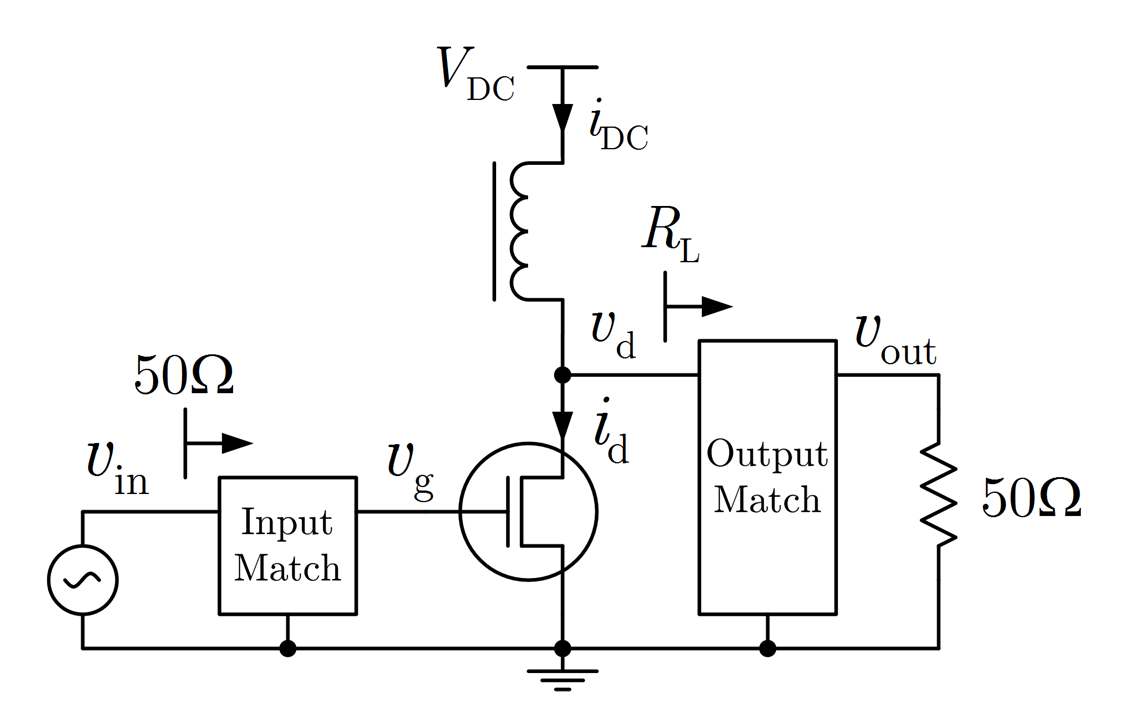
We present an analytical model of the joint linearity-efficiency behavior of radio frequency power amplifiers. The model is derived by Fourier series analysis of a generic amplifier circuit including both strong nonlinearity due to current-clipping as well as weak nonlinearity due to transconductance variation. By selection of the biasing point, common amplifier classes like class A, class B and class AB can be modeled. For numerical evaluation, the model reduces to two lookup-tables, which makes it well suited for high-level system simulations. In an application example we demonstrate how the model can be used to simulate the error-vector-magnitude and the average efficiency for specific single-carrier and multi-carrier modulation schemes. The figure shows a generic circuit of a radio frequency power amplifier. In the paper we used this circuit as the basis for a joint linearity-efficiency model. A Matlab implementation of the model is available at Matlab Central. More information can...
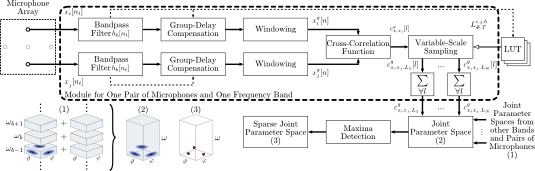
We introduce a new and intuitive algorithm to characterize and localize multiple harmonic sources intersecting in the spatial and frequency domains. It jointly estimates their fundamental frequencies, their respective amplitudes, and their directions of arrival based on an intelligent non-parametric signal representation. To obtain these parameters, we first apply variable-scale sampling on unbiased cross-correlation functions between pairs of microphone signals to generate a joint parameter space. Then, we employ a multidimensional maxima detector to represent the parameters in a sparse joint parameter space. In comparison to others, our algorithm solves the issue of pitch-period doubling when using cross-correlation functions, it estimates multiple harmonic sources with a signal power smaller than the signal power of the dominant harmonic source, and it associates the estimated parameters to their corresponding sources in a multidimensional sparse joint parameter space, which can be directly fed into a tracker. We tested our algorithm and three others...
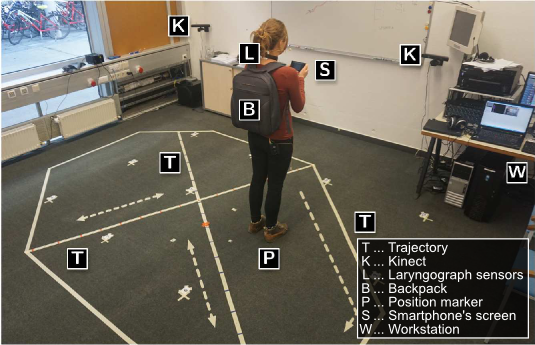
We introduce a unique, comprehensive Austrian German multi-sensor corpus with moving and non-moving speakers to facilitate the evaluation of estimators and detectors that jointly detect a speaker’s spatial and temporal parameters. The corpus is suitable for various machine learning and signal processing tasks, linguistic studies, and studies related to a speaker’s fundamental frequency (due to recorded glottograms). Available corpora are limited to (synthetically generated/spatialized) speech data or recordings of musical instruments that lack moving speakers, glottograms, and/or multi-channel distant speech recordings. That is why we recorded 24 spatially non-moving and moving speakers, balanced male and female, to set up a two-room and 43-channel Austrian German multi-sensor speech corpus. It contains 8.2 hours of read speech based on phonetically balanced sentences, commands, and digits. The orthographic transcriptions include around 53,000 word tokens and 2,070 word types. Special features of this corpus are the laryngograph recordings (representing glottograms required to detect a...
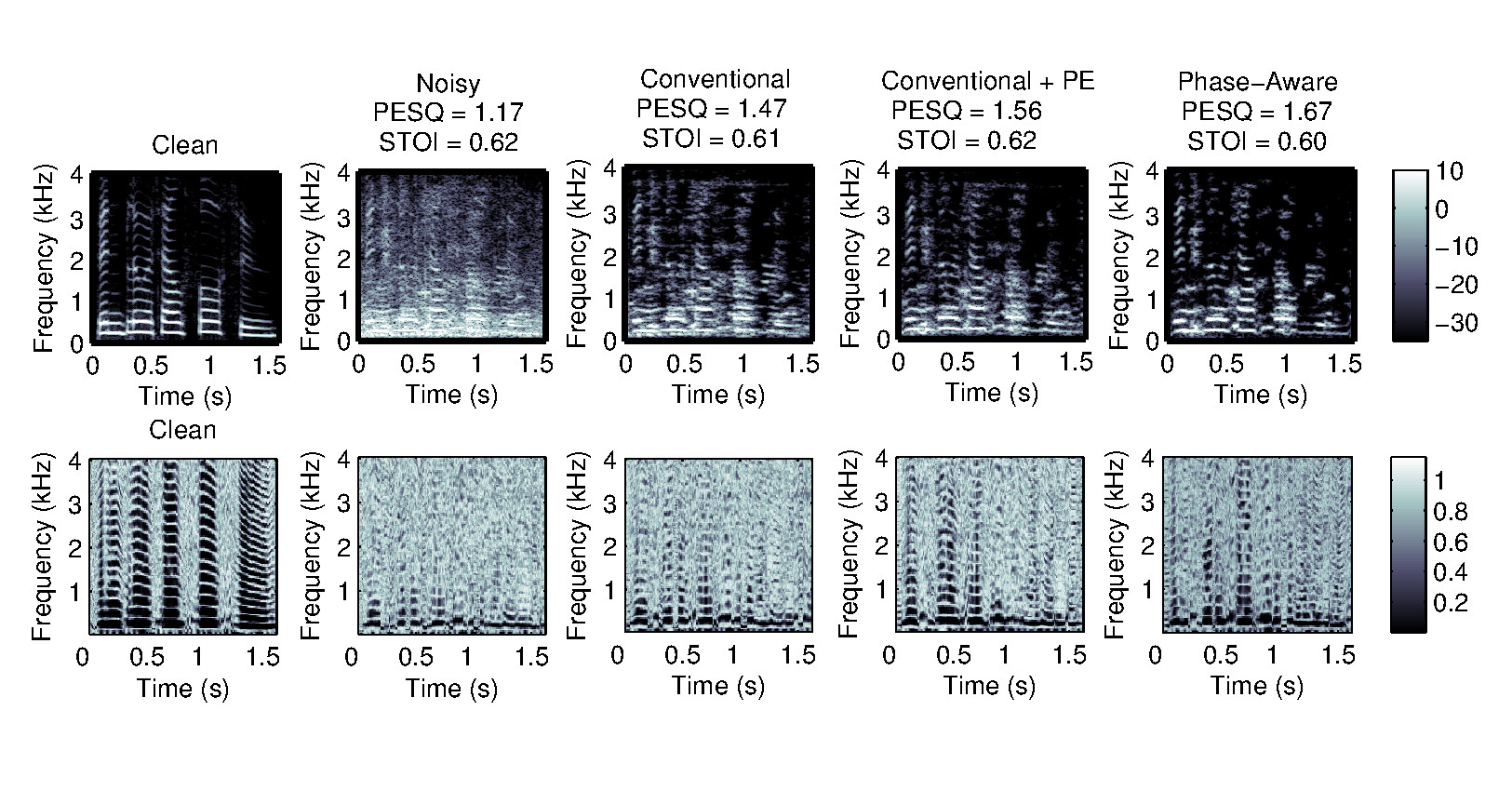
During the past three decades, the issue of processing spectral phase has been largely neglected in speech applications. There is no doubt that the interest of speech processing community towards the use of phase information in a big spectrum of speech technologies, from automatic speech and speaker recognition to speech synthesis, from speech enhancement and source separation to speech coding, is constantly increasing. In this paper, we elaborate on why phase was believed to be unimportant in each application. We provide an overview of advancements in phase-aware signal processing with applications to speech, showing that considering phase-aware speech processing can be beneficial in many cases, while it can complement the possible solutions that magnitude-only methods suggest. Our goal is to show that phase-aware signal processing is an important emerging field with high potential in the current speech communication applications. The paper provides an extended and up-to-date bibliography on the topic...
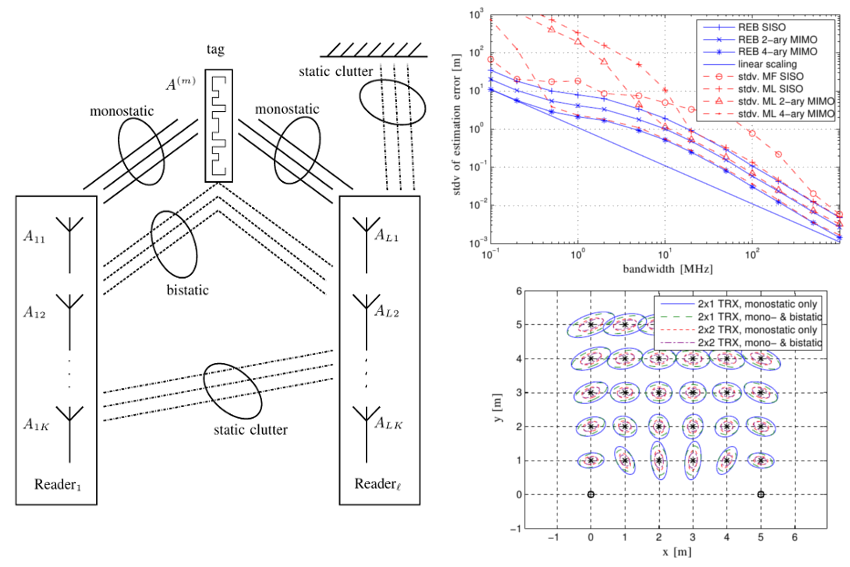
In my research I analyze the achievable ranging and positioning performance for a radio frequency identification (RFID) system. Two design constraints of such a system, (i) the bandwidth of the transmit signal and (ii) the use of multiple antennas at the readers are analyzed in my paper ‘MIMO gain and bandwidth scaling for RFID positioning in Dense Multipath Channels’. The ranging performance is developed for correlated and uncorrelated constituent channels by utilizing a geometry-based stochastic channel model for the downlink and the uplink. The ranging error bound is utilized to compute the precision gain for a ranging scenario with multiple collocated transmit and receive antennas. The position error bound is then split into a monostatic and bistatic component to analyze the positioning performance in a multiple input, multiple output (MIMO) RFID system. Simulation results indicate that the ranging variance is approximately halved when utilizing uncorrelated constituent channels in a monostatic...
During my PhD studies I have introduced and discussed a positioning and tracking system for harsh indoor environments that is aware of its surrounding environment and further is able to act optimally on its environment, i.e. it controls the measurement information-return. The Figure illustrates the schematics of the cognitive positioning/tracking system. The physical main blocks are the cognitive perceptor (CP) and cognitive controller (CC) with built-in memories for the perceived environmental state and the (reciprocally) taken control-actions on the environment. Both are linked via feedback and feedforward information, thus the controller is able to choose new actions based on the perceptor’s Bayesian state information. The perception-action-cycle (PAC) incorporates the sensed environment into the closed loop with the CP and CC. The resulting cognitive multipath-assisted simultaneous localization and mapping algorithm has the following detailed characteristics: – Robust online learning of the geometric-probabilistic environment model (GPEM) –Robustness against outliers in the measurements and...
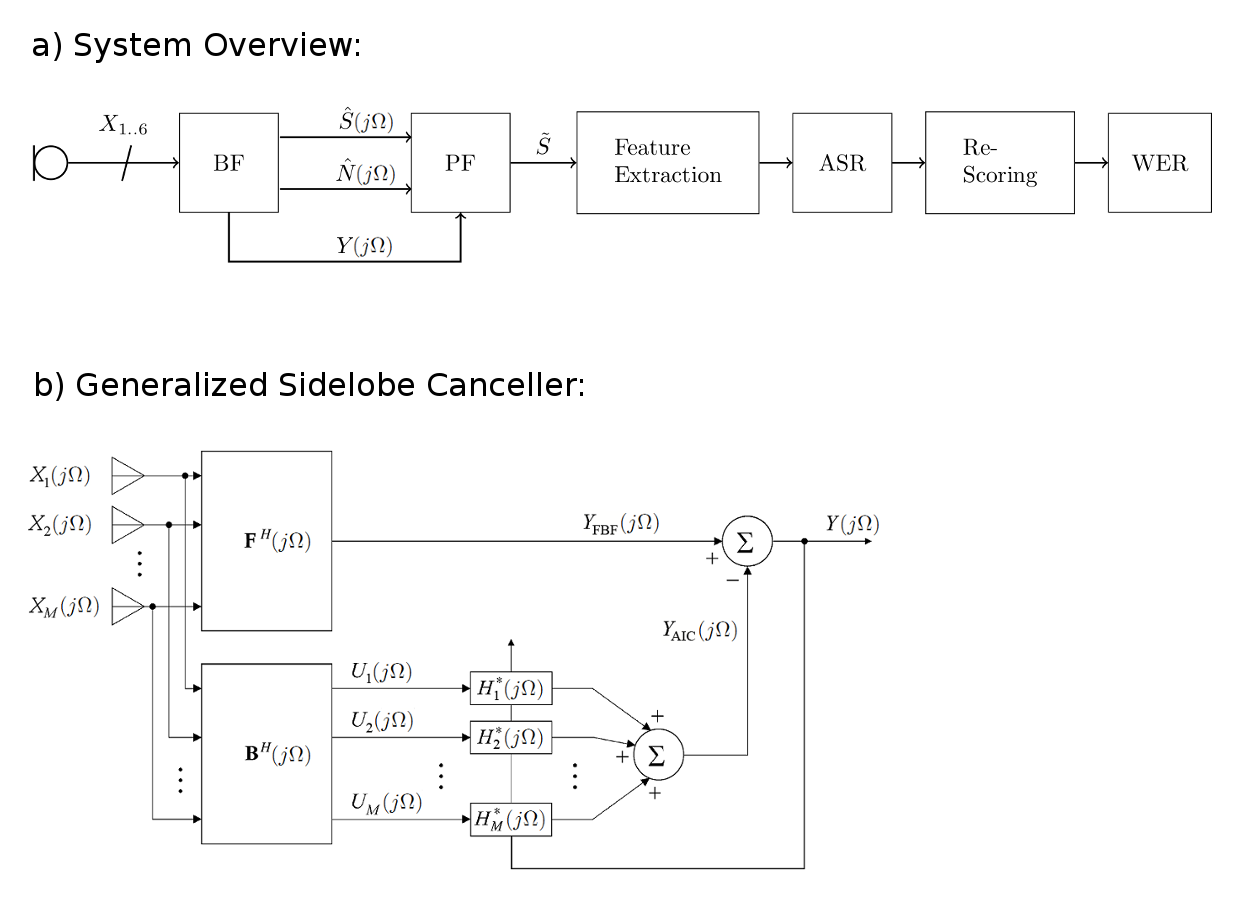
Recognizing speech under noisy condition is an ill-posed problem. The CHiME3 challenge targets robust speech recognition in realistic environments such as street, bus, caffee and pedestrian areas. We study variants of beamformers used for pre-processing multi-channel speech recordings. In particular, we investigate three variants of generalized sidelobe canceller (GSC) beamformers, i.e. GSC with sparse blocking matrix (BM), GSC with adaptive BM (ABM), and GSC with minimum variance distortionless response (MVDR) and ABM. Furthermore, we apply several postfilters to further enhance the speech signal. We introduce MaxPower postfilters and deep neural postfilters (DPFs). DPFs outperformed our baseline systems significantly when measuring the overall perceptual score (OPS) and the perceptual evaluation of speech quality (PESQ). In particular DPFs achieved an average relative improvement of $17.54% OPS points and $18.28% in PESQ, when compared to the CHiME3 baseline. DPFs also achieved the best WER when combined with an ASR engine on simulated development...
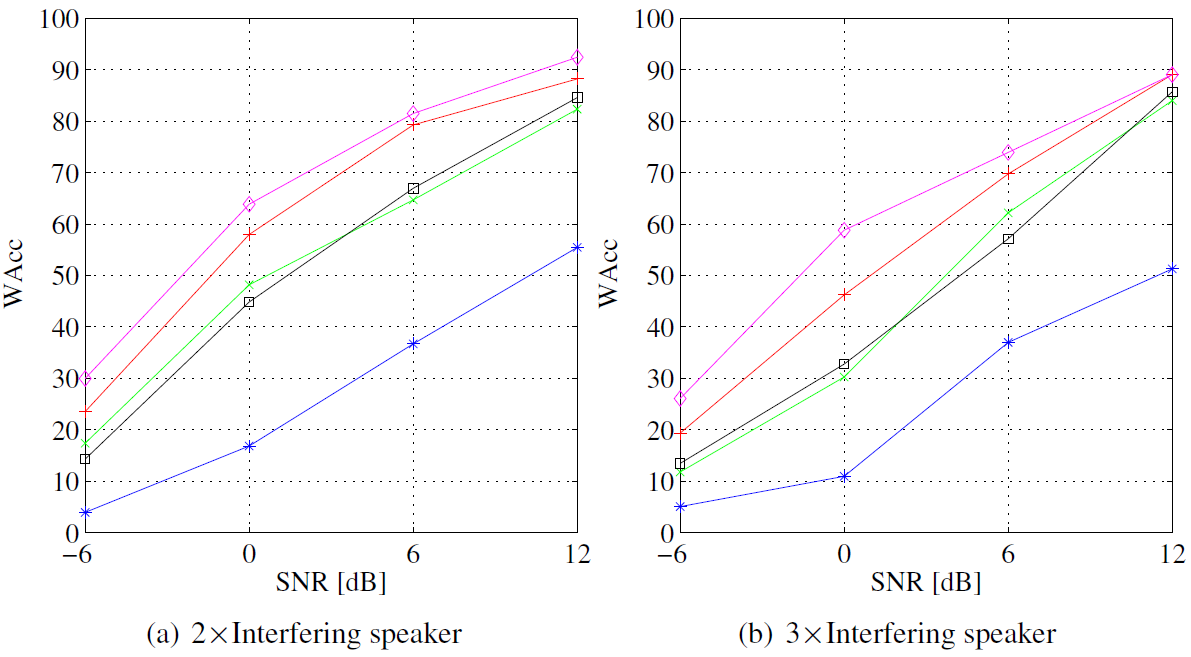
For automatic speech recognition (ASR) systems it is important that the input signal mainly contains the desired speech signal. For a compact arrangement, differential microphone arrays (DMAs) are a suitable choice as front-end of ASR systems. The limiting factor of DMAs is the white noise gain, which can be treated by the minimum norm solution (MNS). In this work, we introduce the first time the MNS to adaptive differential microphone arrays (ADMAs). We compare its effect to the conventional implementation when used as front-end of an ASR system. In experiments we show that the proposed algorithms consistently increase the word accuracy up to 50% relative to their conventional implementations. For PESQ we achieve an improvement of up to 0.1 points. The figure shows the WAcc for speaker scenarios with a target speaker and two or three interfering speakers, for different SNR values. We see that for every scenario and SNR condition all ADMAs increase the WAcc compared to a single omnidirectional microphone front-end. With...
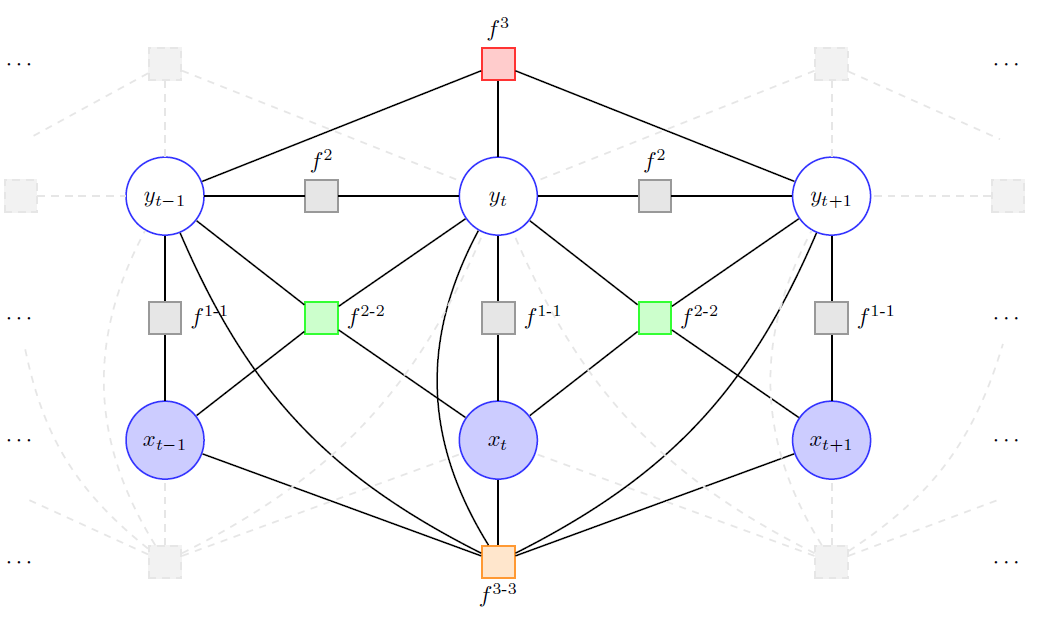
We introduce both joint training of neural higher-order linear-chain conditional random fields (NHO-LC-CRFs) and a new structured regularizer for sequence modelling. We show that this regularizer can be derived as lower bound from a mixture of models sharing parts, e.g. neural sub-networks, and relate it to ensemble learning. Furthermore, it can be expressed explicitly as regularization term in the training objective. We exemplify its effectiveness by exploring the introduced NHO-LC-CRFs for sequence labeling. Higher-order LC-CRFs with linear factors are well-established for that task, but they lack the ability to model non-linear dependencies. These non-linear dependencies, however, can be efficiently modeled by neural higher-order input-dependent factors. Experimental results for phoneme classification with NHO-LC-CRFs confirm this fact and we achieve state-of-the-art phoneme error rate of 16.7% on TIMIT using the new structured regularizer. The work has been presented at this year’s ECML – take a look at the full paper [Ratajczak2015b].
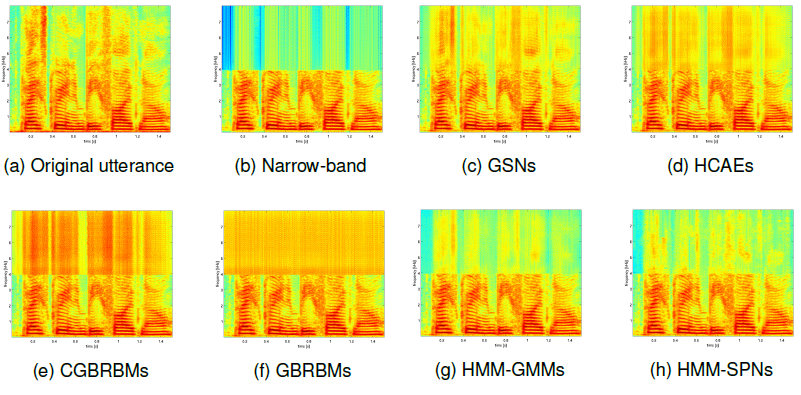
Recently, sum-product networks (SPNs) showed convincing results on the ill-posed task of artificial bandwidth extension (ABE). However, SPNs are just one type of many architectures which can be summarized as representational models. In this paper, using ABE as benchmark task, we perform a comparative study of Gauss Bernoulli restricted Boltzmann machines, conditional restricted Boltzmann machines, higher order contractive autoencoders, SPNs and generative stochastic networks (GSNs). Especially the latter ones are promising architectures in terms of its reconstruction capabilities. Our experiments show impressive results of GSNs, achieving on average an improvement of 3.90dB and 4.08dB in segmental SNR on a speaker dependent (SD) and speaker independent (SI) scenario compared to SPNs, respectively. The figure shows the log-spectogram of the utterance ‘‘Place green in b 5 now’’, spoken by s20 recovered by various frame-wise SD deep representation models and hybrid HMM models: (a) original full bandwidth signal; narrow bandwidth signal (b); GSNs...
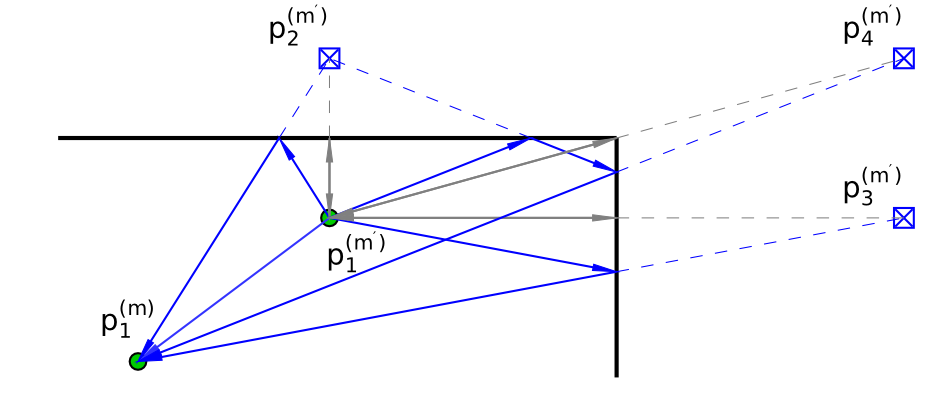
Wireless localization has become a key technology for cooperative agent networks. However, for many applications, it is still illusive to reach the desired level of accuracy and robustness, especially in indoor environments which are characterized by harsh multipath propagation. In this work we introduce a cooperative low-complexity algorithm that utilizes multipath components for localization instead of suffering from them. The algorithm uses two types of measurements: (i) bistatic measurements between agents and (ii) monostatic (bat-like) measurements by the individual agents. Simulations that use data generated from a realistic channel model, show the applicability of the methodology and the high level of accuracy that can be reached. The figure shows an illustration of multipath geometry using VAs for (i) bistatic transmissions (blue) between an agent m and m’_and for (ii) a _monostatic measurement (gray) by agent m.

We explore neural higher-order input-dependent factors in linear-chain conditional random fields (LC-CRFs) for sequence labeling, i.e. the fusion of two powerful models. Higher-order LC-CRFs with linear factors are well-established for sequence labeling tasks, but they lack the ability to model non-linear dependencies. These non-linear dependencies, however, can be efficiently modelled by neural higher-order input-dependent factors which map sub-sequences of inputs to sub-sequences of outputs using distinct multilayer perceptron sub-networks. This mapping is important in many tasks, in particular, for phoneme classification where the phone representation strongly depends on the context phonemes. Experimental results for phoneme classification with LC-CRFs and neural higher-order factors confirm this fact and we achieve the best ever reported phoneme classification performance on TIMIT, i.e. a phoneme error rate of 15.8%. Furthermore, we show that the success is not obvious as linear high-order factors degrade phoneme classification performance on TIMIT. The work has been presented at this...
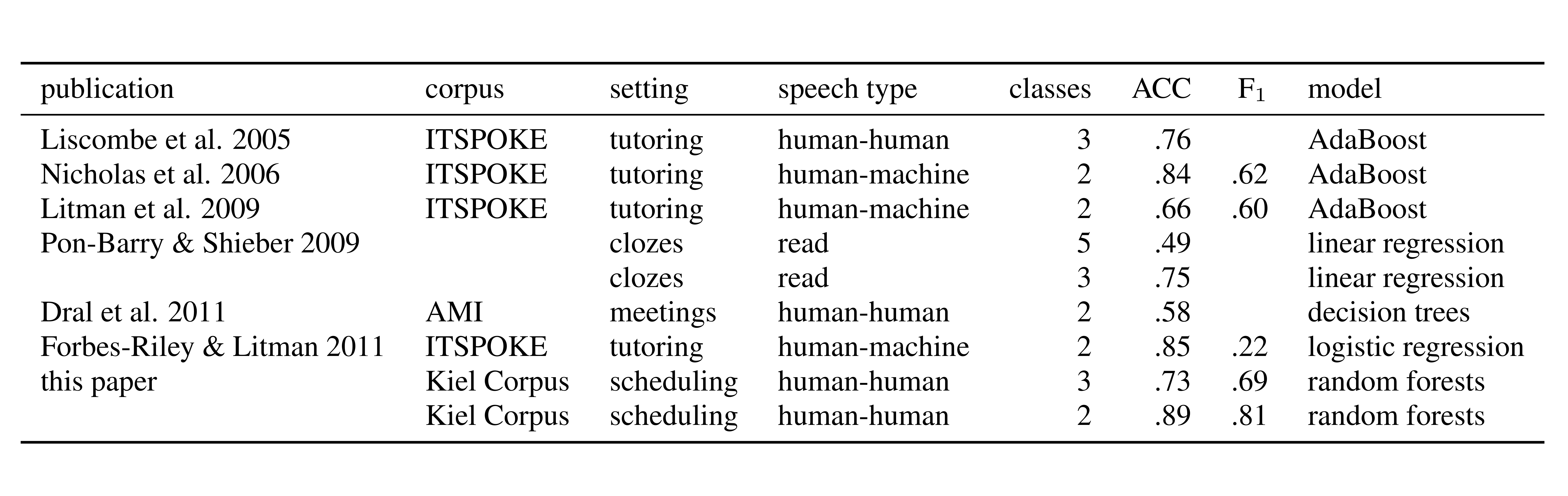
In this paper, we automatically detected uncertainty in naturalistic spontaneous German human-human conversations. We presented an approach which is based on linguistic, paralinguistic and extralinguistic features. We tested 9 feature classes (timing, fundamental frequency, intensity, spectrum, voice quality, lexicon, syntax, dialogue structure, external features) and evaluated their performance on 1158 dialogue acts taken from the spontaneous part of the Kiel Corpus. The results showed that it is possible to detect uncertainty in speech automatically relatively reliably. The accuracy with which this task is accomplished depended heavily on the feature set employed. In particular, our more complex modelling of speech rate contributed to good classification performance. Automatic feature selection could improve performance even though the machine learning algorithm employed in this paper is built to handle highly correlated features spaces. While only 64 features in size, the resulting feature set outperformed all other feature sets. Even though all features implemented in...

In December 2014 we successfully finished our international project entitled ‘Distant-speech Interaction for Robust Home Application’, also known as DIRHA. Our main goal was to set up a prototype in our laboratory that could be controlled by Austrian German speech interaction. We would like to present the prototype by showing you a video. It is about an application of this distant-speech interacting system’s prototype named DIRHA. Two attendees control lights and blinds by interacting with the system acoustically. They activate it by saying a keyword and instruct it to do something. In case of unclear or ambiguous instructions, the system automatically asks specific questions leading to answers containing the required information.

Followed up by the special session organized last year at INTESPEECH, Dr. Pejman Mowlaee together with Dr. Rahim Saeidi and Prof. Yannis Stylianou have proposed special issue entitled “Phase-Aware Signal Processing in Speech Communication” to EURASIP Speech Communication. The detailed information about the special issue is available at EURASIP website. Further information about the important deadlines and aims and scope of this special issue is available on Elsevier website. More recent updates, audio examples and progresses made towards phase-aware signal processing are available here. For an overview on phase-aware signal processing in speech communication see our special session paper published at INTERSPEECH last year found here. The description of the special issue is as follow: In the past decades, the amplitude of speech spectrum is considered to be the most important feature in different speech processing applications and phase of the speech signal has received less attention. Recently, several findings...
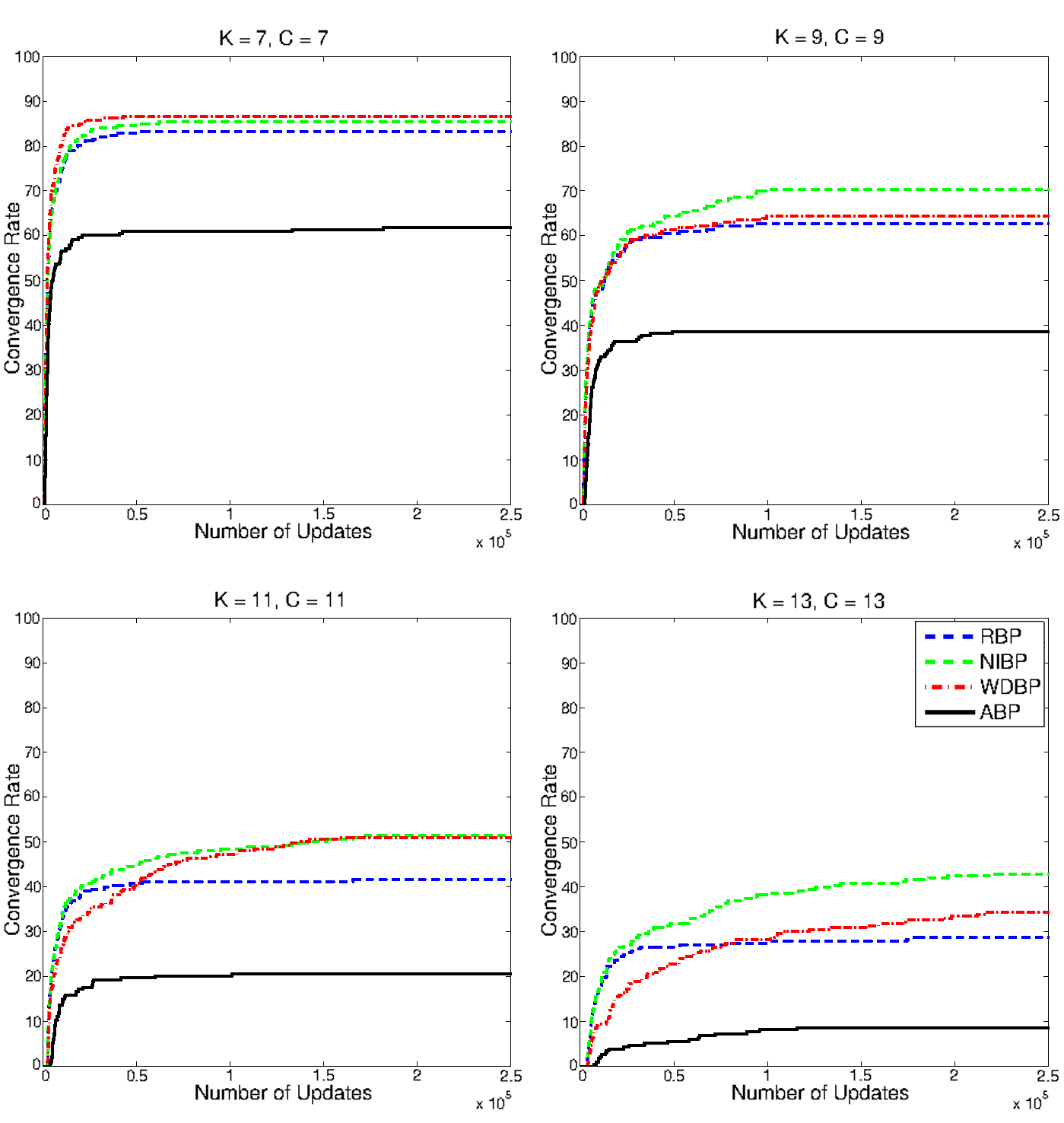
The influence of different message update schemes on belief propagation (BP) highlights the need of designing an appropriate message scheduling. Yet, Residual belief propagation (RBP) is the only established method utilizing this observation and consequently increasing the convergence rate. We observed that RBP fails to converge if local oscillations occur and the same messages are repeatedly updated. We propose two novel methods to prevent and correct such oscillations. First we show how noise injection belief propagation (NIBP) detects oscillating messages and adds random noise to improves the convergence rate. The second method, weight decay belief propagation (WDP), applies a damping on the residual to gradually reduce the relevance of these messages and consequently forces convergence. Additionally, in contrast to previous work, we consider the correctness of the obtained marginals and present the remarkable performance increase on a variety of synthetic problems. The figure shows the rate of convergence on graphs...
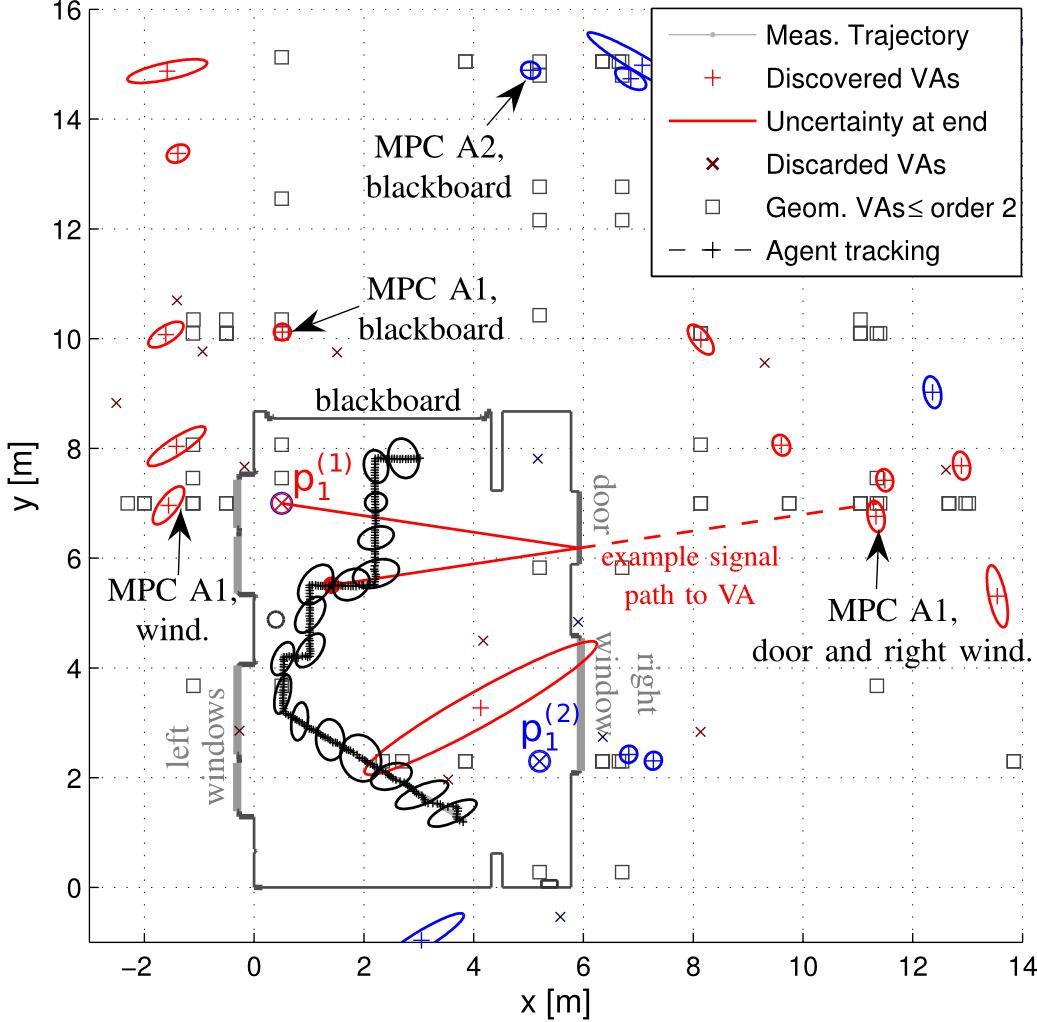
In this work, we propose a new simultaneous localization and mapping (SLAM) approach that allows to learn the floor plan representation and to deal with inaccurate information. A key feature is an online estimated channel characterization that enables an efficient combination of the measurements. Starting with just the known anchor positions, the proposed method includes the virtual anchor (VA) positions also in the state space and is thus able to adapt the VA positions during tracking of the agent. Furthermore, the method is able to discover new potential VAs in a feature-based manner. The work presents a proof of concept using measurement data. The excellent agent tracking performance of 90 % of the error lower than 5 cm achieved with a known floor plan can be reproduced with SLAM. The figure illustrates the SLAM approach followed in this work. Two anchors at p11 and p12 represent the infrastructure. The agent position as well as the floor plan (represented by VAs)...
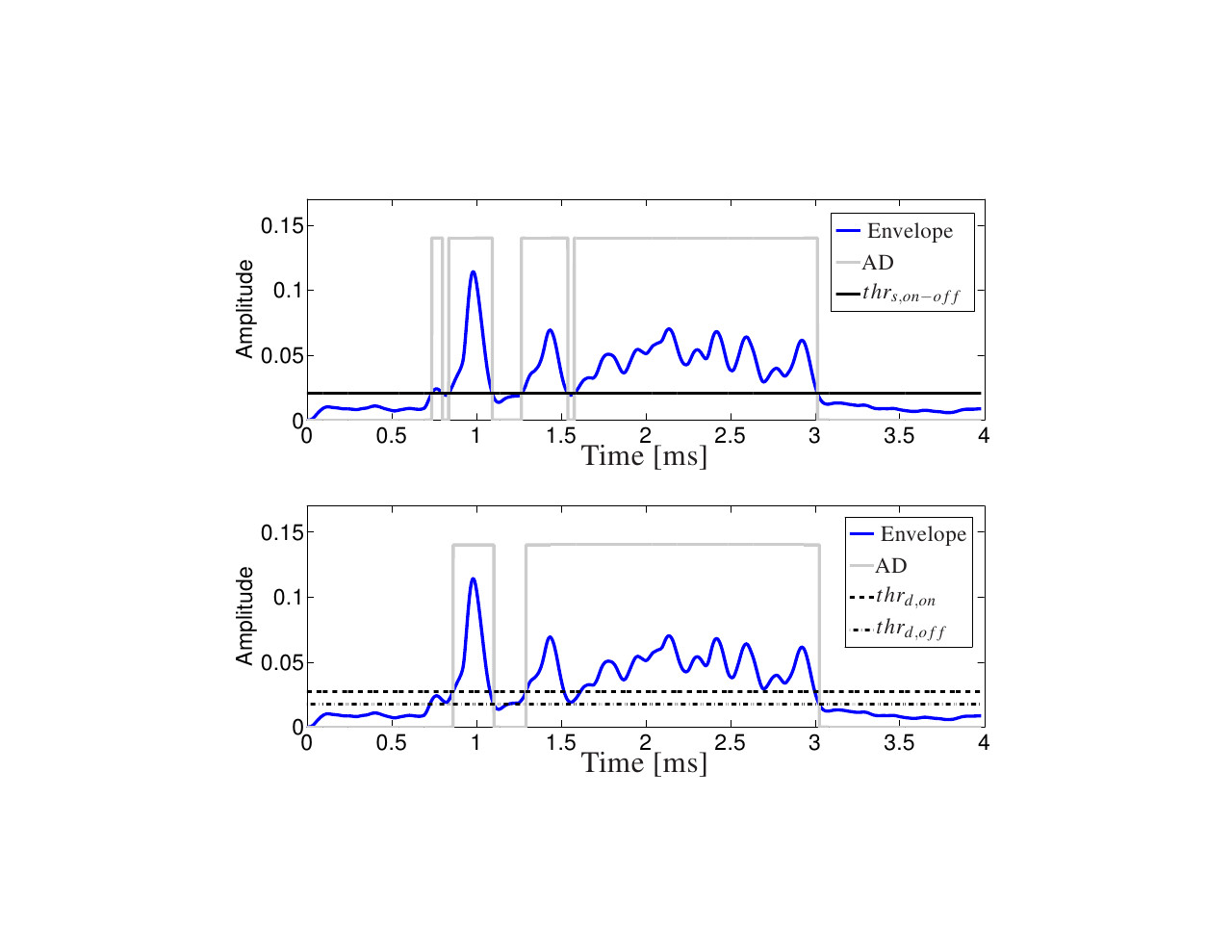
In this work we use electromyographic (EMG) signals to investigate speech/non-speech detection for EL speech. The muscle activity, which is represented by the EMG signal, correlates with the intention to produce speech sounds and therefore, the short-term energy can serve as a feature to make a speech/non-speech decision. We developed a data acquisition hardware to record EMG signals using surface electrodes. We then recorded a small database with parallel recordings of EMG and EL speech and used different approaches to classify the EMG signal into speech/non-speech sections. We compared the following envelope calculation methods: root mean square, Hilbert envelope, and low-pass filtered envelope, and different classification methods: single threshold, double threshold and a Gaussian mixture model based classification. In the figure you can see activity detection (AD) using the recorded EMG signals during speech production. The upper plot shows single threshold detection and the lower plot double threshold detection. Conclusion:...
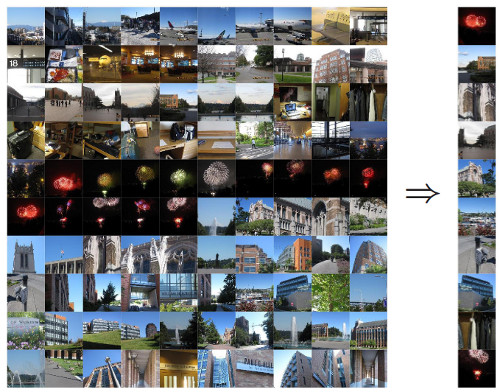
We address the problem of image collection summarization by learning mixtures of submodular functions. Submodularity is useful for this problem since it naturally represents characteristics such as fidelity and diversity, desirable for any summary. Several previously proposed image summarization scoring methodologies, in fact, instinctively arrived at submodularity. We provide classes of submodular component functions (including some which are instantiated via a deep neural network) over which mixtures may be learnt. We formulate the learning of such mixtures as a supervised problem via large-margin structured prediction. As a loss function, and for automatic summary scoring, we introduce a novel summary evaluation method called V-ROUGE, and test both submodular and non-submodular optimization (using the submodular-supermodular procedure) to learn a mixture of submodular functions. Interestingly, using non-submodular optimization to learn submodular functions provides the best results. We also provide a new data set consisting of 14 real-world image collections along with many human-generated...
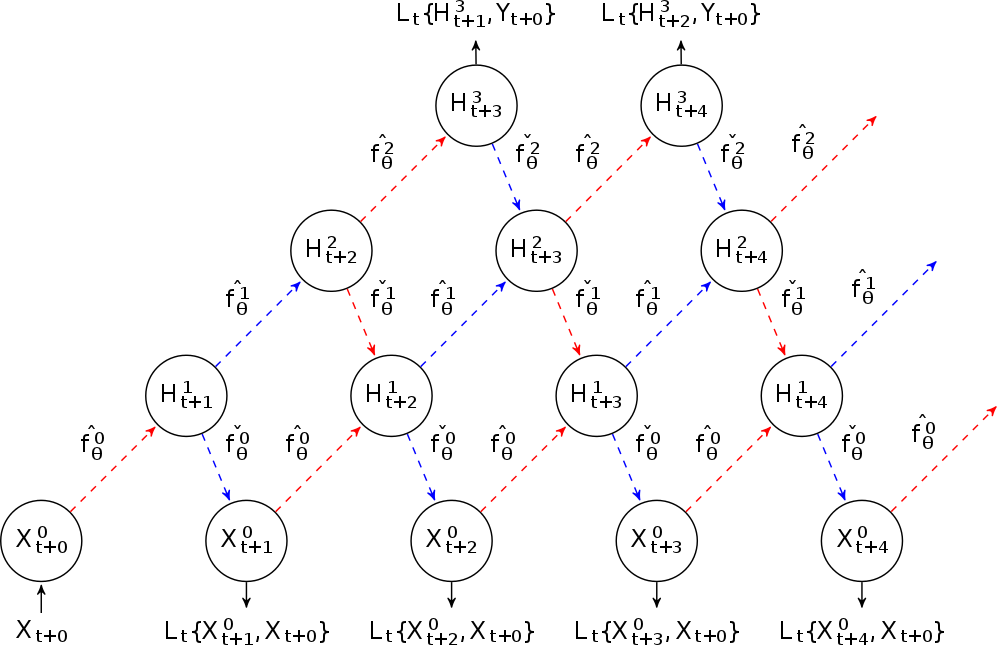
We extend generative stochastic networks to supervised learning of representations. In particular, we introduce a hybrid training objective considering a generative and discriminative cost function governed by a trade-off parameter λ. We use a new variant of network training involving noise injection, i.e. walkback training, to jointly optimize multiple network layers. Neither additional regularization constraints, such as 1, 2 norms or dropout variants, nor pooling- or convolutional layers were added. Nevertheless, we are able to obtain state-of-the-art performance on the MNIST dataset, without using permutation invariant digits and outperform baseline models on sub-variants of the MNIST and rectangles dataset significantly. The figure shows a GSN Markov chain for input Xt+0 and target Yt+0 with backprop-able stochastic units.
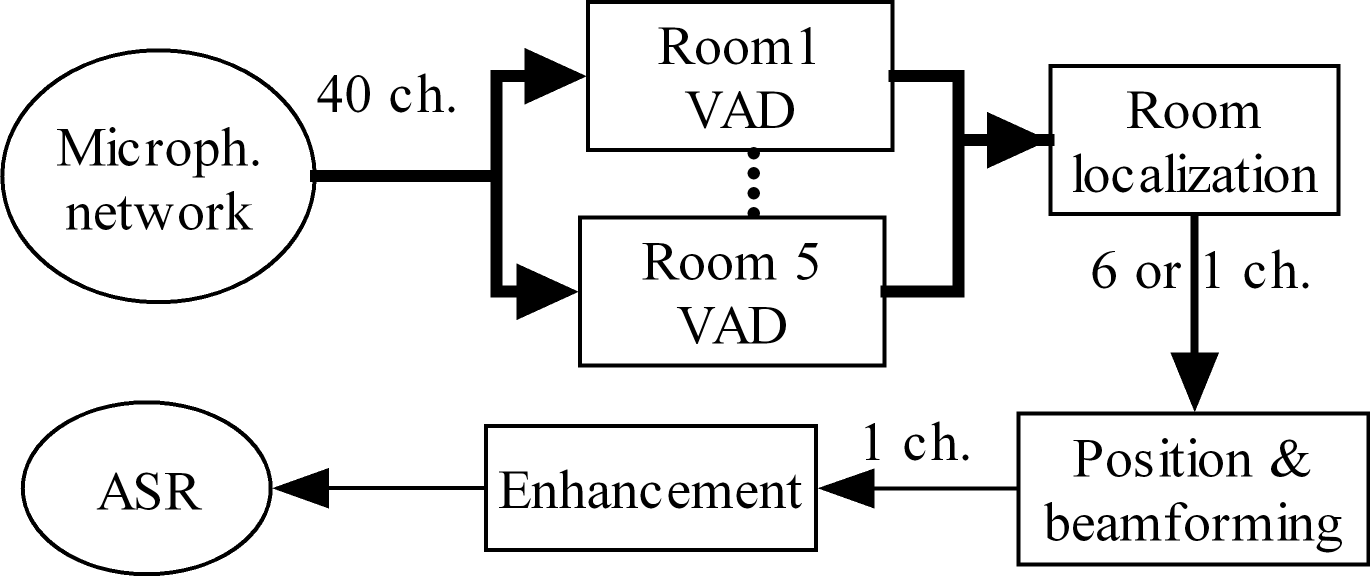
The problem of room localization is to determine where, in a multi-room environment, a person is producing a speech utterance. At Interspeech 2014 we have presented the system of the figure. It exploits the information gained from a network of microphones installed in house, where the lack of calibration of the microphone energies creates an additional challenge. The Word-Accuraccy (WAcc) of the baseline (based on just identifying the room where the VADs detects the maximum energy) is 79 %. The WAcc of the proposed system (based on a LDA classifier with high-SNR-energy+coherence as input feature) improves to 90%.

Our lab is responsible for the audio recording of dinner table talk at Concordia station in the Antartica for the European Space Agency sponsored project CAPA (Psychological Status Monitoring by Content Analysis and Acoustic- Phonetic Analysis of Crew Talks and Video Diaries). The Concordia station is run by the French Polar Institute (Institut Paul Emile Victor, IPEV) and the Italian Antarctic Research Programme (PNRA). Concordia is one of the most remote places on earth. In the antarctic winter, which lasts from mid February to mid November, the station cannot be accessed from outside. This means the winter-over team of 10-15 people is locked in the station and has to deal with isolation, sun-light deprivation and other challenges. Our project analyses the dinner talks and tries to infer the psychological state of the crew members from the speech. The SPSC Lab will be separating the speakers and enhancing the sound quality....
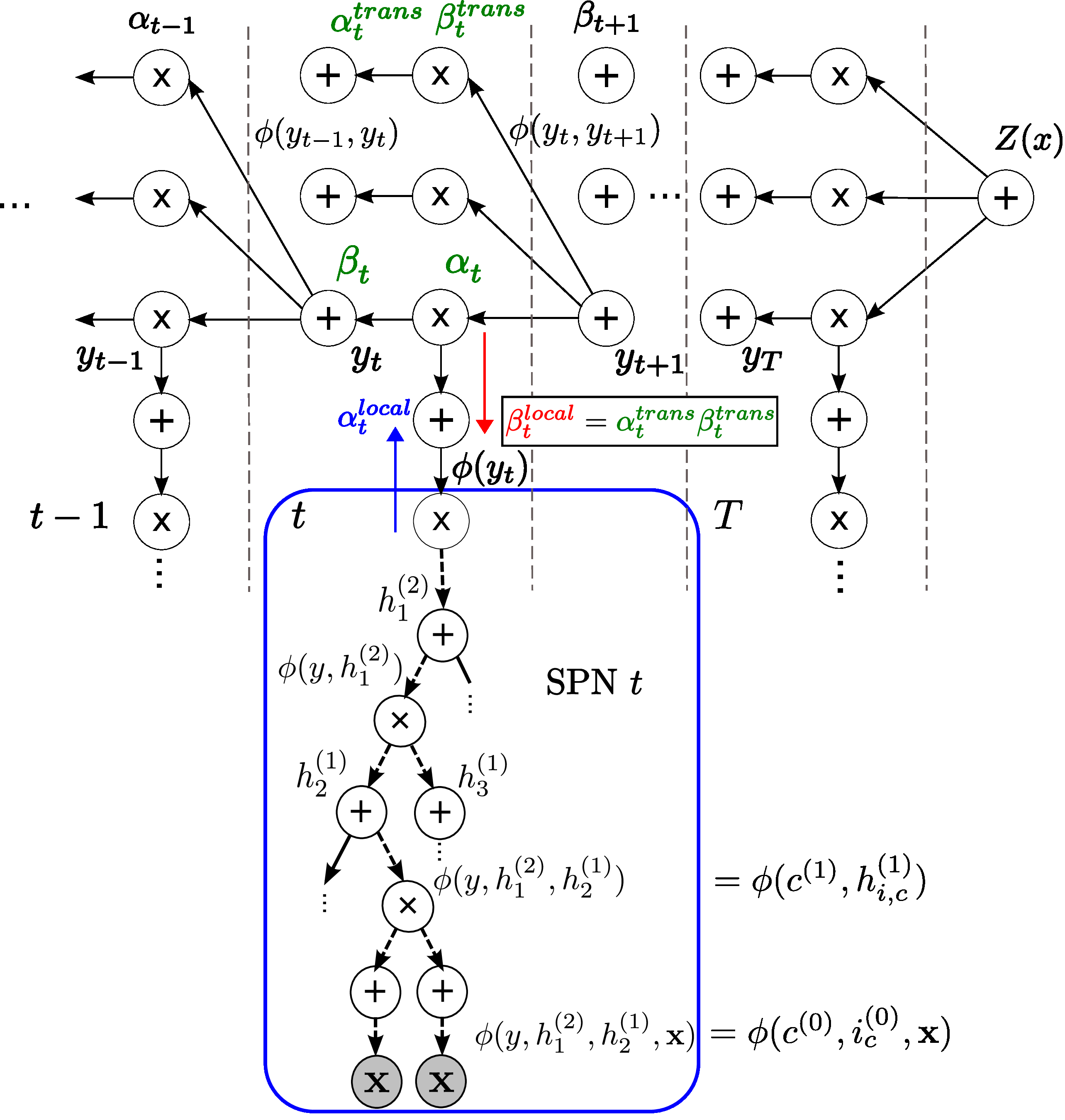
Linear-chain conditional random fields (LC-CRFs) have been successfully applied in many structured prediction tasks. Many previous extensions, e.g. replacing local factors by neural networks, are computationally demanding. In this paper, we extend conventional LC-CRFs by replacing the local factors with sum-product networks, i.e. a promising new deep architecture allowing for exact and efficient inference. The proposed local factors can be interpreted as an extension of Gaussian mixture models (GMMs). Thus, we provide a powerful alternative to LC-CRFs extended by GMMs. In extensive experiments, we achieved performance competitive to state-of-the-art methods in phone classification and optical character recognition tasks. The work has been presented at this year’s ICML Workshop (Learning Tractable Probabilistic Models) – take a look at the full paper [Ratajczak2014].
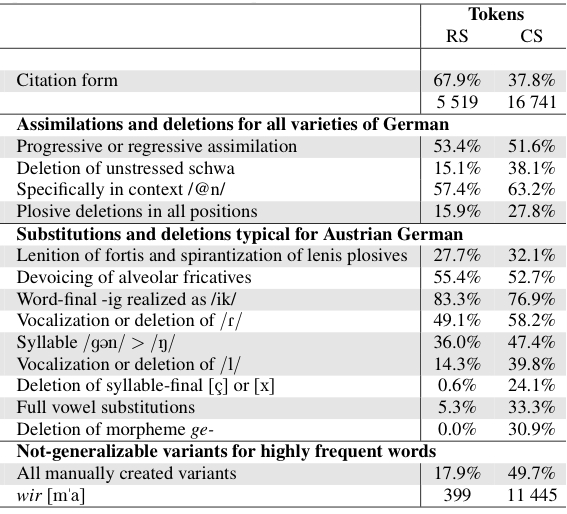
Whereas for the varieties of German spoken in Germany, conversational speech has been given noticeable attention in the fields of linguistics and automatic speech recognition (ASR), for conversational Austrian there is a lack in speech resources and tools as well as phonetic studies. Based on the recently collected GRASS corpus, we provide rule-based methods for the creation of a pronunciation dictionary and an ASR-supported automatic method for the creation of broad phonetic transcriptions of conversational Austrian German. Our comparative analysis based on these transcriptions showed that whereas only 33.1% of the tokens in read speech show variation from the canonical transcription, this number raises to 63.2% in conversational speech. In the future, we will perform more detailed analysis concerning the conditions for pronunciation variation and incorporate our findings into models of automatic speech recognition. The table shows a summary of our analysis on the frequencies of occurrence of a large...
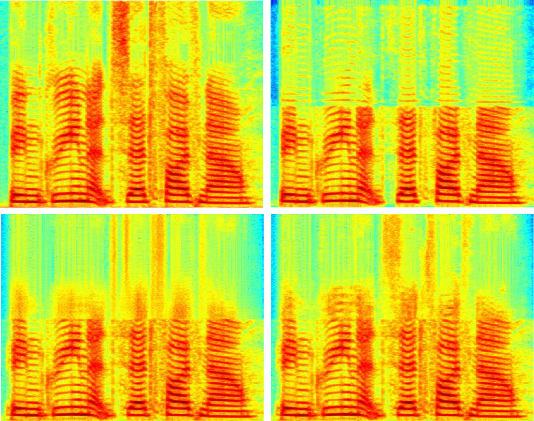
Sum-Product networks (SPNs) are a recently proposed deep network architecture for representing probability distributions. They allow a high degree of dependency among the random variables, while still allowing efficient inference. In particular, SPNs showed convincing results on the ill-posed problem of image completion, i.e. predicting missing parts of an image given the observed part. We applied SPNs to the related task of artificial bandwidth extension, i.e. recovering the lost high frequencies in telephone speech, using the observed telephone low-band. To this end, we incorporated SPNs as observation models in hidden Markov models and used most-probable explanation (MPE) inference for reconstructing the lost frequency bins. The extended signals have a natural high-frequency structure in the spectrogram, and improve the state-of-the art in terms of log-spectral distortion and in informal listening tests. The upper left figure shows the original spectrogram of the example utterance: ‘Bin green at zed 5 now’. The upper...
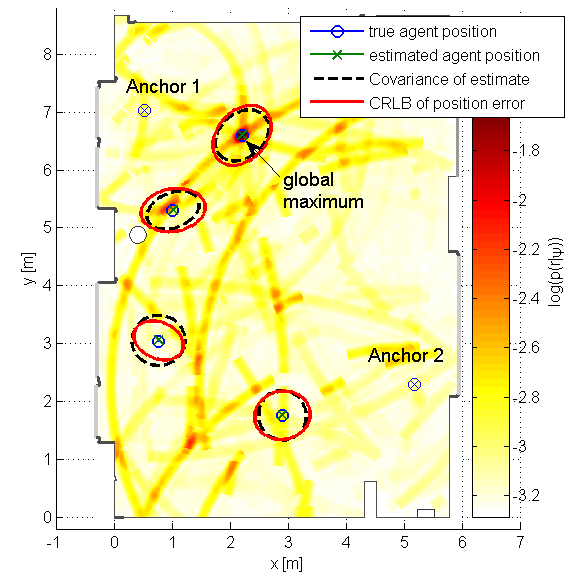
Multipath-assisted indoor positioning (using ultra-wideband signals) exploits the geometric information contained in deterministic multipath components. With the help of a-priori available floorplan information, robust localization can be achieved, even in absence of a line-of-sight connection between anchor and agent. In a recent work, the Cramer-Rao lower bound has been derived for the position estimation variance using a channel model which explicitly takes into account diffuse multipath as a stochastic noise process in addition to the deterministic multipath components. In this work, we adapt this model for position estimation via a measurement likelihood function and evaluate the performance for real channel measurements. To find the global maximum of the highly multi-modal LHF, we introduced a particle filter method with swarm behavior optimization (PF-PSO). Performance results confirm the applicability of this approach and show the importance of considering diffuse multipath. Evaluations, using real measurement data, have shown that the orientation and size...
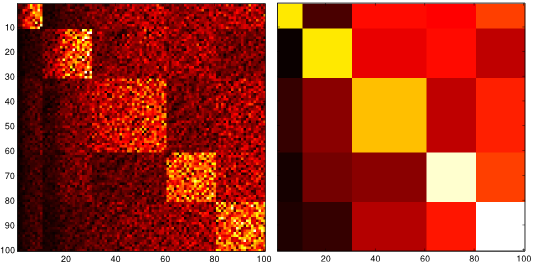
Many scientific disciplines, such as systems biology or natural language processing, suffer from Markov chains with exploding state spaces. Markov aggregation, i.e., finding a Markov chain on the partition of the original state space, is one way to reduce the computational complexity of the model. We provide an information-theoretic cost function for the problem of Markov aggregation and show that the information bottleneck method, a popular technique in machine learning, can be used to find a solution iteratively. The cost function we use is an upper bound on the Kullback-Leibler divergence rate between the aggregated Markov chain and the stationary process obtained by projecting the original Markov chain through the partition function. The latter is not Markov in general; if it is, the original chain is called lumpable w.r.t. the partition function. By defining the cost function appropriately, it can be shown that the solution is closely related to lumpability...

Both research in the field of linguistics and speech technology require the existence of large speech corpora, recorded at sufficiently high quality and transcribed at least at the orthographic level, which can be used for the generation of further annotation layers (e.g., phonetic, morphological, syntactic and/or prosodic level). Since for Austrian German the available speech material was very limited, we have recently created the GRASS corpus, the first corpus of read and conversational Austrian German. GRASS contains phonetically balanced sentences, commands elicited by pictures, key words, telephone numbers and one hour of free conversations produced by 38 speakers originating from one of the mayor cities of eastern Austria (Graz, Linz, Salzburg, Vienna). Super-wideband recordings enable the simulation of different acoustic environments by filtering the speech material with different measured room impulse responses. Orthographic transcriptions were created manually and include the annotation of breathing, hesitations and laughter. More information can be...
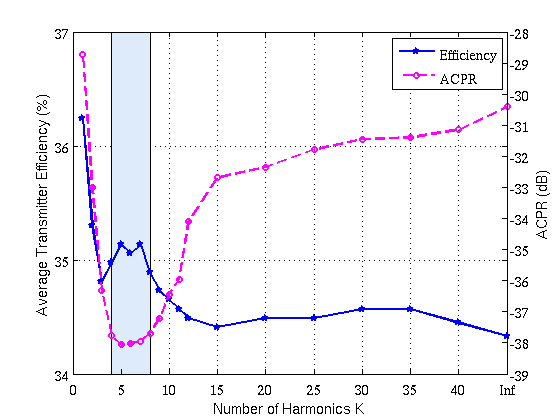
Coding efficiency is an important measure of burst-mode RF transmitters. In our recent publication [1] we have proposed an aliasing-free PWM (AFPWM) method which can avoid all destructive aliasing distortion due to the sampling process when the PWM process is performed in digital domain. A side effect of AFPWM method is that it induces amplitude variations onto the amplitude of the generated PWM signals. On the one hand, the non-ideal switching amplitude can cause nonlinear distortion due to the clipping effect, where a possible way to minimize the ripple is to choose an appropriate number of harmonics in the generated PWM signals. On the other hand, with the AFPWM method, the PA is operated over a slightly wider range of output power regions instead of operating at saturation and in cut-off, resulting in a reduced RF PA efficiency. In this work [2], we show that the AFPWM method does not...
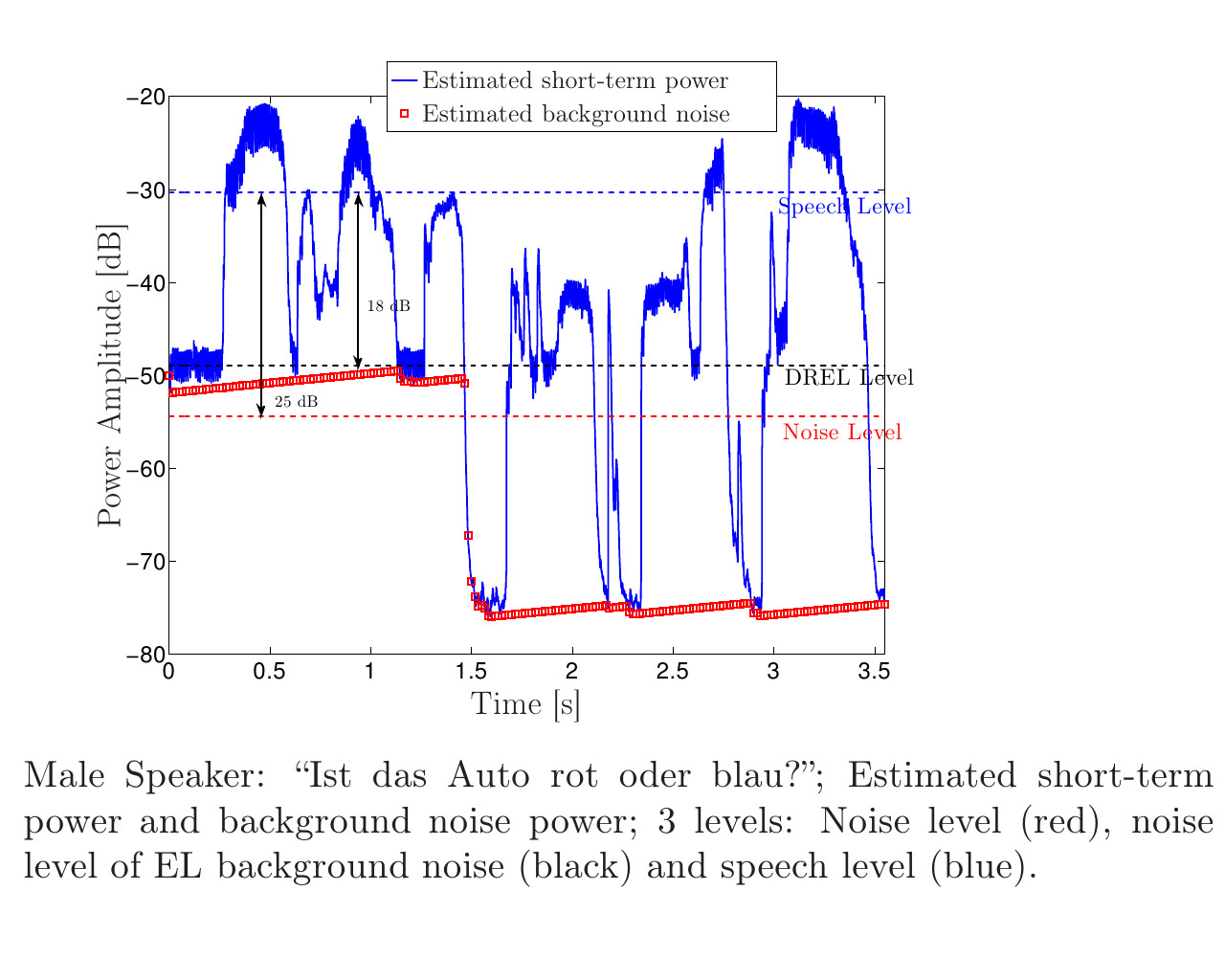
Experi ment s: In this paper, we describe the German parallel Electro-Larynx speech – Healthy speech (ELHE) Corpus which has been recorded in our recording studio. 3 female and 4 male healthy subjects recorded up to 500 sentences spoken one time with healthy speech (HE) and one time using the Electro-Larynx (EL) device. Analyses of signal-to-noise ratios (SNR) have shown the following: For HE speech only two levels (noise and speech) can be distinguished but there are three different levels inherent in EL speech (see figure): noise, direct-radiated noise from the EL device (DREL) and speech (corrupted with DREL). First-order IIR smoothing was used to estimate the short-term power of the signal and of the noise whereas the DREL level was found using an iteratively changing threshold. _Conclusion: Statistical analyses have shown that the length of EL sentences is longer than for HE sentences. Moreover, the fundamental frequency f0 of...
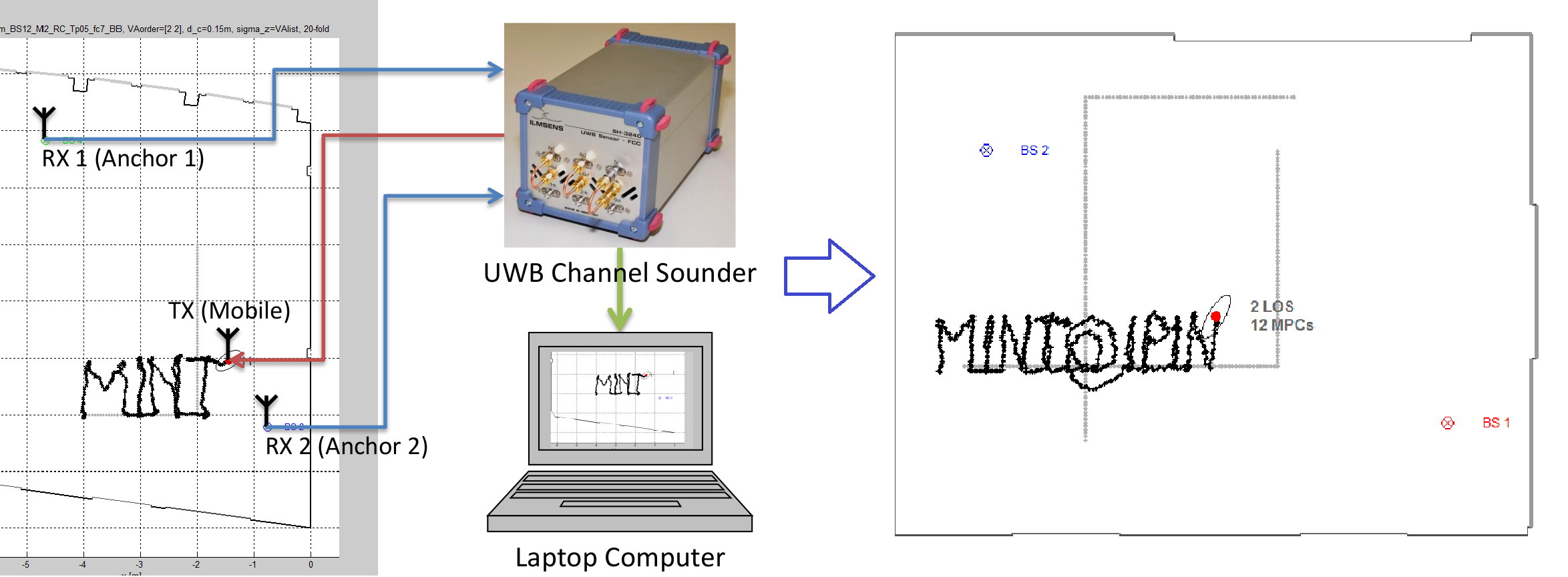
At this years’ International Conference on Indoor positioning and Indoor Navigation (IPIN2013), a real-time demonstration of multipath-assisted indoor navigation and tracking (MINT) has been presented. Using an M-sequence based ultra-wideband (UWB) channel sounder, a mobile user is tracked exploiting the geometric structure of deterministic multipath components (MPCs). The plot shows the hardware setup and a tracking result in a roughly 4x5m room, demonstrating the centimeter-level accuracy. This demonstration shows the benefits and challenges of this approach: On the one hand, deterministic MPCs carry a significant amount of position-related information that can increase both accuracy and robustness of tracking algorithms. This is especially relevant in non-line-of-sight (NLOS) situations, which are the most important performance impairments for radio-based indoor localization systems still today. On the other hand, the problem is challenging as reliable detection of MPCs and data association are required. This demonstration shows real-time algorithms that allow for systematic exploitation of...
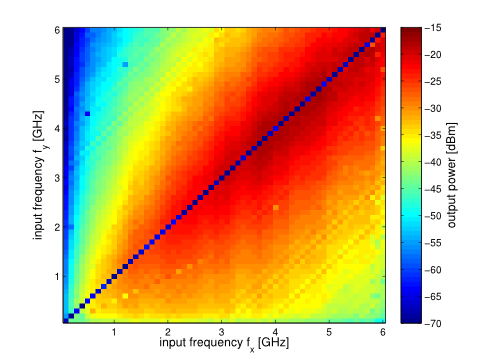
Analog multipliers are employed in many applications. In RF front-ends, for example, they are widely used for frequency conversion tasks. For noncoherent receivers such as energy detectors or transmitted-reference front-ends, they need to be able to multiply arbitrary (broadband) input signals. Unfortunately, there exist no ideal hardware realization of such devices, hence they inevitably create undesired signal content at their output. To be able to deal with these effects or correct for them, we need to be able to model and identify realistic RF multipliers. We proposed and validated an accurate multiple-input single-output Wiener-Hammerstein model for ultra-wideband analog multipliers. The model consist of input and output filters and a bivariate polynomial kernel that can model accurately ultra-wideband analog multipliers. The model is flexible and, due to its structure, gives insight in the behavior of such devices. Additionally it provides the possibility to study the realistic behavior of systems involving those...

Sum-Product Networks are a novel type of graphical models, which can represent complex variable interaction, still allowing efficient inference. They show especially convincing results in reconstruction tasks, i.e. predicting missing parts of data given partial evidence. The image shows from top to bottom: original image, covered image, reconstruction using Poon & Domingos’ SPN algorithm (2011), Dennis & Ventura’s algorithm (2012), and our recently proposed Greedy Part-wise SPN learning algorithm. Due to the generative nature of the trained SPNs, they can be applied for versatile inference: the same model can reconstruct the top part, left part, or any other selection of missing variables. For more information, see our recent ECML PKDD paper Greedy Part-Wise Learning of Sum-Product Networks.
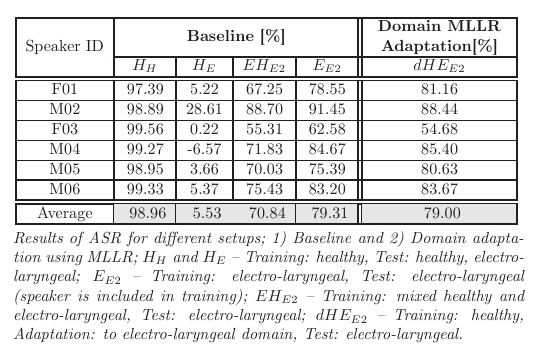
In this work we apply disordered speech, namely speech produced by an Electro-Larynx (EL), on an Automatic Speech Recognition (ASR) system which was designed for normal, healthy speech. When disordered speech is applied to ASR systems, the performance will significantly decrease. ASR systems are increasingly becoming part of daily life. Therefore, the word accuracy rate of disordered speech should be reasonably high to make ASR technologies accessible for patients suffering from speech disorders. Experiments: In the table, word accuracy (WAcc) rates are shown for different setups. The WAcc, when training material only consists of healthy speech and we test on healthy speech, is 98.96% (Baseline - HH). When the test is carried out on electro-laryngeal speech, the performance is very low (5.53%; Baseline - HE) due to the mismatched domain. When speech material of electro-laryngeal speech is added to the healthy training, (EHE2) the word accuracy rate improves to 70.84%...
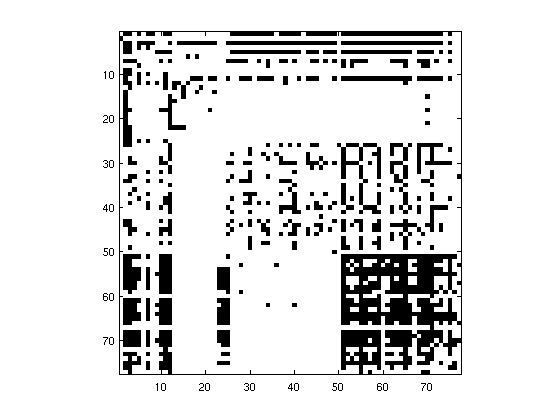
In a recent research collaboration with the Department of Mathematical Structure Theory, we characterized state space aggregations of Markov chains which preserve the information contained in the model. Moreover, we presented an information-theoretic characterization of lumpability, i.e., of the phenomenon that a non-injective function of a Markov chain can be a Markov chain of higher order. These characterizations, together with a set of sufficient conditions on the transition graph of the Markov chain, where employed for lossless model order reduction. In particular, we trained a letter bi-gram model based on F. Scott Fitzgerald’s text “The great Gatsby” (see the figure for the adjacency matrix of the model; for example, the transitions between lower-case letters on the bottom right can be seen). Applying our algorithm to this model, we identified an aggregation of states which is not only information-preserving, but which renders the output process a second-order Markov chain. With the...
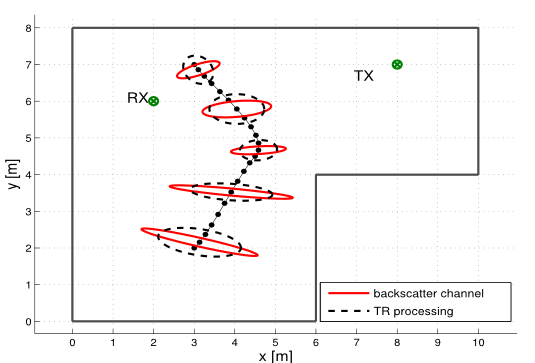
In this work, we derive the Cramer-Rao lower bound (CRLB) on the position error for an RFID tag positioning system exploiting multipath. The channels constituting the backscatter radio system are modeled with a hybrid deterministic/stochastic channel model. In this way, both the geometry of the deterministic multipath components (MPCs) and the diffuse multipath are taken into account properly. Computational results show the influence of the room geometry on the bound and the importance of the diffuse multipath in dense indoor environments. Time reversal (TR) processing using the deterministic MPCs is analyzed as one possibility to overcome the degenerate nature of the backscatter channel. A derivation and evaluation of the corresponding CRLB shows the potential gain of TR processing as well as its strong dependence on the geometry. The figure shows the position error ellipses for the forty-fold standard deviation for several trajectory positions, in red for the backscatter channel alone...
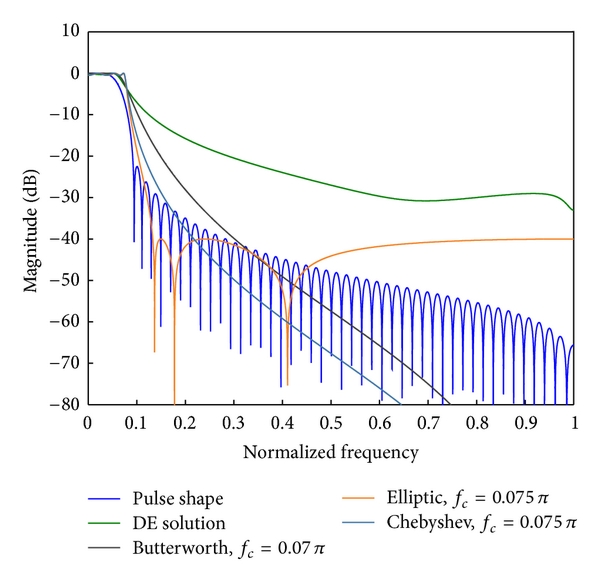
Digital IIR filter implementations are important building blocks of most communication systems. Conventionally, the filters are specified via amplitude and phase in the frequency domain as given by the matched filter theory. Digital filter implementations, nonlinear analog components and channel characteristics introduce a multitude of additional effects, though. These are not taken into account by the matched filter theory. Which, in turn, leads to results providing a rough estimate, at best. Our work reforms the design process, defines the system’s bit error rate as the main objective and searches the huge – yet finite – filter design space for suitable coefficients. The figure shows the magnitude responses of conventional filter designs (Butterworth, elliptic, and Chebyshev) and contrasts it with the magnitude response of the solution identified by differential evolution (in green). Observe that the optimal solution’s gain is significantly higher than the filter specification derived from the matched filter assumption...
The measurement of pitch marks (PMs) is an important part of voice assessment. In diplophonic voice (i.e., a pathologic voice with two pitches) PM determination is crucial, and its validity needs special attention. Hence, a new approach for PM determination from Laryngeal High-Speed Videos (LHSVs), rather than from audio signals is proposed. In this novel approach, double PMs instead of traditional single PMs are extracted from a diplophonic voice sample, in order to account for double fundamental frequencies. The dominant oscillation frequencies of the vocal folds are extracted by spectral analysis of LHSVs with respect to time. Unit pulse trains with these frequencies are created as PM trains and compensated for the phase shift. The PMs are compared to Praat’s single audio PMs. It is shown that double PMs are needed in order to analyze diplophonic voice, because traditional single PMs do not explain its double-source characteristic. The figure shows...
The utilization of a burst-mode PA together with pulse-width modulation (PWM) is a promising concept for achieving high efficiency in radio frequency (RF) transmitters. Nevertheless, such a transmitter requires bandpass filtering to suppress side-band spectral components to retrieve the wanted signal, which reduces the transmit power and the transmitter efficiency. To boost efficiency for signals with high PAPRs and signals at variable transmit power levels, burst-mode multilevel transmitters have been widely discussed as a potential solution. This work describes an efficiency optimization procedure of burst-mode multilevel transmitters for signals with high PAPRs and signals at variable transmit power levels. The impact of the threshold value on the transmitter efficiency is studied, where the optimum threshold value and the maximum transmitter efficiency can be obtained according to input magnitude statistics. Simulations are used to validate the efficiency improvement of the optimized burst-mode multilevel transmitters compared to two-level and non-optimized multilevel transmitters. ...
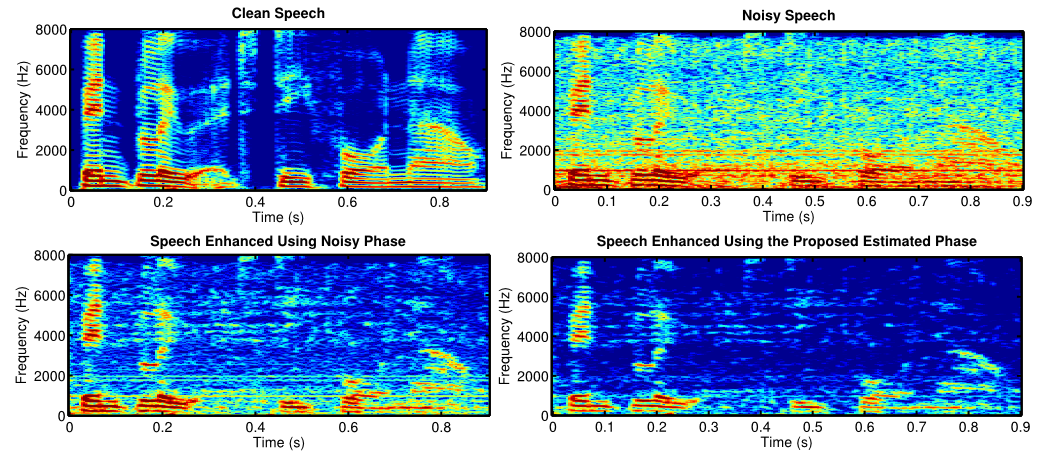
In many speech processing applications, the spectral amplitude is the dominant information while the use of phase spectrum is not so widely spead. In [6] we present an overview on why speech phase spectrum has been neglected in the conventional techniques used in different applications including speech enhancement and source separation. Recovering a target speech signal from a single-channel recording falls into two groups of methods: 1) single-channel speech separation, and 2) single-channel speech enhancement algorithms. While there has been some success in either of the groups, all of them frequently ignore the issue of phase estimation in their parameter estimation and signal reconstruction. Instead, they directly pass the noisy signal phase for reconstructing the output signal which leads to certain perceptual artifacts in the form of musical noise and cross-talk in speech enhancement and speech separation scenarios, respectively. To address the phase impacts on single-channel speech enhancement/separation algorithms, we...
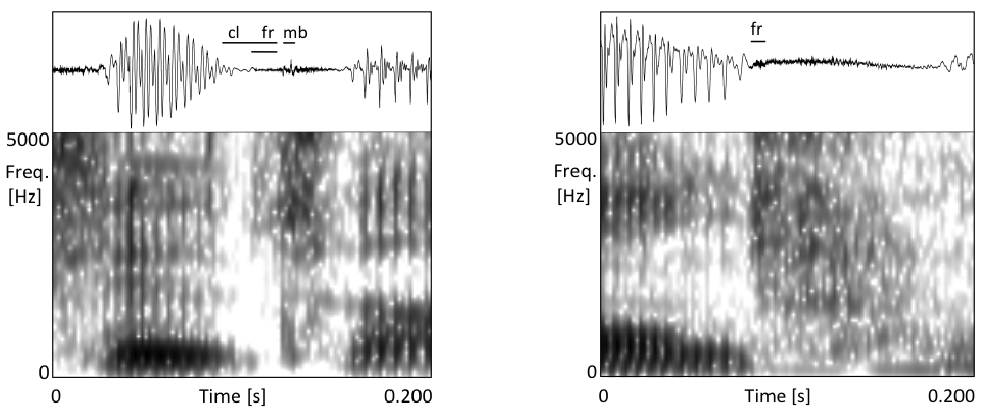
In conversational speech words are often realized in a reduced way compared to their citation forms. One frequent process in Germanic languages is the deletion of word-final /t/. The German word und_for instance, is often pronounced as _un. In a series of studies, we investigated the role of reduced plosives for human perception compared to its role for automatic speech processing. In a corpus of Dutch spontaneous conversations, we found that 25% of all final /t/ tokens are completely acoustically absent and that 11.5% of the tokens are produced canonically. This means, that most of the tokens (63.5%) are realized as something in between, not completely absent, but also not fully present. We defined a set of sub-phonemic features for analyzing these realizations of /t/, some of them shown in the figures above (cl = closure, fr = alveolar friction, mb = multiple burst). Even though these examples of /t/...
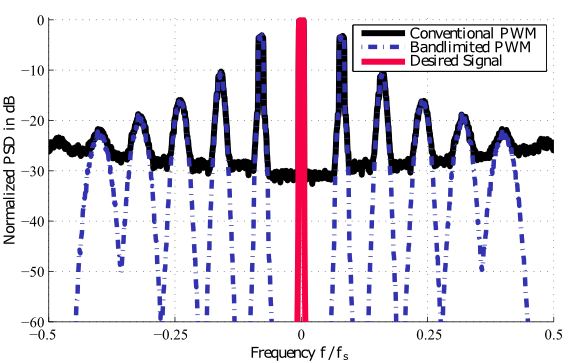
Digital pulse-width modulation (PWM) is used to encode a nonconstant-envelope signal into a train of rectangular pulses with varying widths, such that the information lying in the amplitude of the input signal is represented by the widths of the pulses. Pulsed signals can be used to drive the power amplifier in burst-mode RF transmitters. After amplification, the desired signal, which is the amplified passband equivalent of the input to the pulse-width modulator, has to be recovered by a bandpass filter. However, when generating PWM digitally, a considerable amount of distortion can be observed in and around the band of the desired signal, which prevents perfect signal recovery after amplification. Therefore, conventional PWM is unsuitable for the use in burst-mode RF transmitters. In our work we analyze PWM mathematically. We use a Fourier series to obtain an analytical closed-form equation completely describing the PWM process. With that equation, we can show...

The SPSC Studio is the key facility in educating students in audio recording and related fields. Quite a number of labs and seminars are held there, electro-acoustics, room-acoustics and digital-audio-technology labs as well as recording-studio-technology lab and recording practices to name just a few. In the last weeks, following a process of rethinking workflows and restructuring the concept of its signal flow, it was equipped with a new Lawo mc2 66 mixing-desk. Being one of the most widely used console in broadcast and large scale recording and events, this new console enables the students to be educated on the tools, they will meet in their carrier after graduation. The Lawo console, as the centerpiece of the studio, also marks a new era in signal-routing and processing within the studio: with 8192 connection points on the routing matrix it allows most flexible signal routings, managing a total of 32 AES3 in/32...
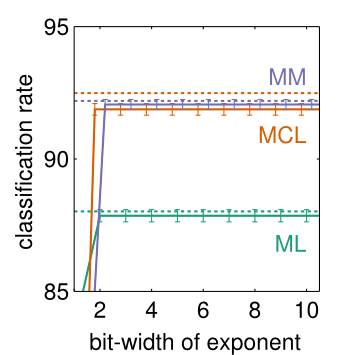
Bayesian network classifers (BNCs) are probabilistic classifers showing good performance in many applications. They consist of a directed acyclic graph and a set of conditional probabilities associated with the nodes of the graph. These conditional probabilities are also referred to as parameters of the BNCs. According to common believe, these classifers are insensitive to deviations of the conditional probabilities under certain conditions. The first condition is that these probabilities are not too extreme, i.e. not too close to 0 or 1. The second is that the posterior over the classes is significantly different. We investigated the effect of precision reduction of the parameters on the classifcation performance of BNCs. The probabilities are either determined generatively or discriminatively. Discriminative probabilities are typically more extreme. However, our results indicate that BNCs with discriminatively optimized parameters are almost as robust to precision reduction as BNCs with generatively optimized parameters. Furthermore, even large precision reduction does...
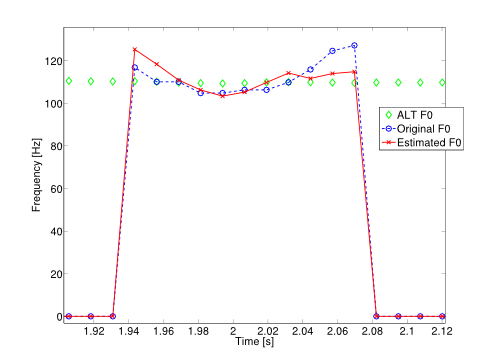
The Artificial Larynx Transducer (ALT) is a possibility to re-obtain audible speech for people who had to undergo an operation where the vocal folds are removed. For decades it is known that the resulting speech suffers from several problems such as a very poor speech quality and an unnatural sound of the speech. One reason for the lack of naturalness is the constant vibration of the ALT and a method to substantially improve ALT speech is to introduce a varying fundamental frequency (F0) - contour. In this work we present a new method to automatically learn an artificial F0-contour. The F0-contour is estimated using a Gaussian mixture model (GMM) which describes the joint density of fundamental frequency and feature vector. To train the GMM a speech database is recorded which contains the same sentences spoken one time with the ALT and one time with healthy speech. The features (MFCCs) for...
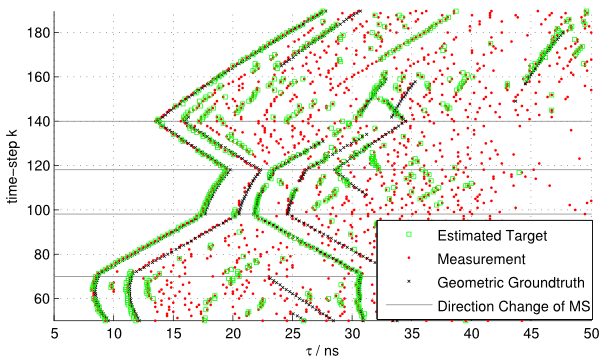
For indoor navigation and tracking using ultra wideband (UWB) radio signals, explicit use of the present multipath propagation can be made. Then, the multipath components (MPCs) need to be extracted from the measured channel impulse response (CIR). In this work we present a method to simultaneously estimate and track the number of MPCs present together with their individual state from measured CIR data using the Probability Hypothesis Density (PHD) multi-target filter. It is shown that the PHD filter is capable of jointly estimating the number of MPCs together with their delays in a challenging indoor scattering scenario. Most of the diffuse scatter components and measurement noise is mitigated by the PHD filter, while most of the estimated MPCs can be matched to a geometrically determined groundtruth of first and second order specular reflections. In the figure, the targets (the MPCs) estimated from the PHD-filter based on the input measurements are...
In this work we use Affine Arithmetic (AA) to estimate the rounding error of different floating-point dot-product implementations. Two floating-point dot-product architectures - a sequential dot-product and a parallel (binary-tree) dot-product - are considered over a wide range of parameters. It is shown that an AA-based probabilistic bounding operator is able to provide a tighter rounding error bound compared to existing techniques. Furthermore, the analytical models for the rounding errors of different floating-point dot-product architectures are derived. As the estimated rounding error bounds are then used for bit width allocation for hardware implementations, the presented error models are key to floating-point code generators and efficient design space exploration. The figure presents the contour maps of the maximum rounding error (dashed lines) obtained by extensive simulations and the AA-based probabilistic rounding error bound (solid lines) of the sequential dot-product. We observe that regardless of the vector length or precision, the AA-based probabilistic bounds are very...
In this work, the hardware implementation of a noncoherent multichannel autocorrelation UWB receiver (AcR) is addressed. We focus on the multiplication device, which is a core part of the AcR and introduces strong interference due to nonlinear effects. To analyze the signal-to-interference ratio performance of the receiver system, a combined Wiener-Hammerstein system model of the multiplication device is introduced. It is shown that the receiver performance strongly depends on the input power of the nonideal multiplier devices. The figure illustrates the signal-to-interference-and-noise-ratio (SINR) of the decision variable of the AcR receiver. Due to nonlinear effects of the multiplier device, the SINR degrades strongly for increasing multiplier input power. The system model proposed in the paper shows that the nonlinear terms introduced by the nonideal multiplier are additive, therefore additional postprocessing might be able to enhance the SINR and BER of the receiver system. For more information, please refer to our...
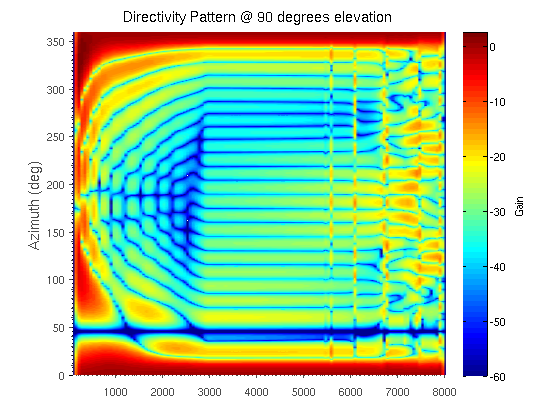
Beamforming is crucial for distant-speech recognition to mitigate causes of system degradation, e.g., interfering noise sources or competing speakers. We introduced adaptations of state-of-the-art broadband data-independent and data-dependent beamformers to uniform circular arrays (UCA), such that competing speakers are attenuated sufficiently for distant speech recognition. The newly introduced multiple null synthesis robust least squares frequency invariant beamformer (MNS-RLSFI) is a data-independent beamformer which enables null-placement in the directions of competing speakers. It is based on convex optimization methods that determine the weighting coefficients. The figure illustrates the directivity pattern of the MNS-RLSFI based on a 24-element UCA, a steering direction of 0 degrees, and a localized competing speaker at 45 degrees. Our experiments show that data-independent beamformers feature a better performance than data-dependent beamformers in case of double-talk scenarios in reverberant environments. According to our results, the delay-and-sum beamformer is the most robust beamformer which exhibits the highest improvements in...
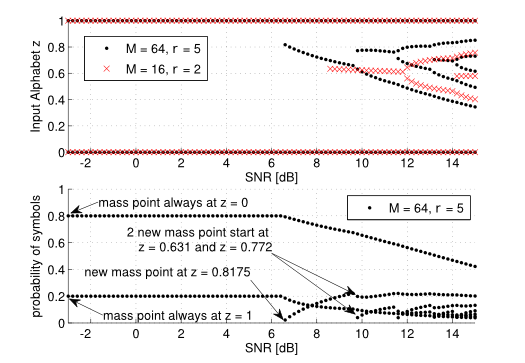
This work presents the channel capacity and capacity-achieving input distribution of an energy detection receiver structure. Using the Blahut-Arimoto algorithm combined with a particle method, the positions and probabilities of the optimal mass points were found. It was shown that the capacity increases with decreasing noise dimensionality M and increasing peak-to-average power ratio (PAPR, parameter r in figure) and that the achieving input distribution is discrete with a finite number of mass points. The figure shows the positions and probabilities of the mass points of the capacity-achieving input distribution over the SNR for different PAPR and noise dimensionality M. The average and peak power are constraints to the transmitted modulation alphabet and the noise dimensionality M is the product of the integration time and the receiver bandwidth of the energy detector. The simulation results have shown that the optimal input distribution, if an AP and PA constraint are applied, is...
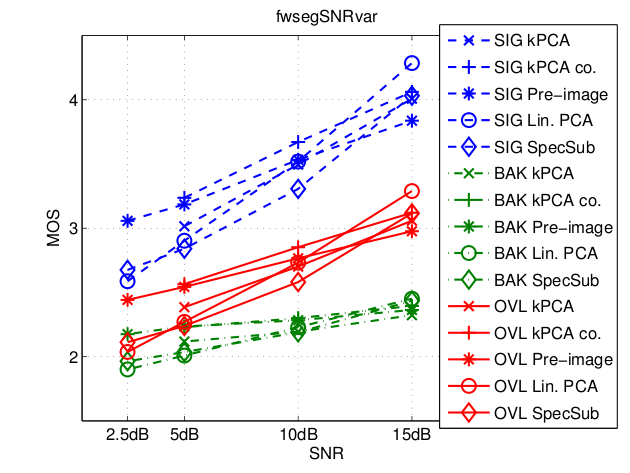
In this work, we show how to de-noise speech in the complex spectral domain using pre-image iterations. The method is derived from kernel principal component analysis (kPCA). Instead of applying PCA in a high-dimensional feature space and then going back to the original input space by using a solution to the pre-image problem, only the pre-image step is applied for de-noising. We show that the de-noised audio sample is a convex combination of the noisy input data and that the resulting algorithm is closely related to the soft k-means algorithm. Compared to kPCA, this method reduces the computational costs while the audio quality is similar and speech quality measures do not degrade. The figure presents a comparison of the results from pre-image iterations (Pre-image) to the results of kernel PCA (kPCA), kernel PCA with combined pre-imaging (kPCA co.), linear PCA (Lin. PCA), and spectral subtraction (SpecSub) using a variant of...
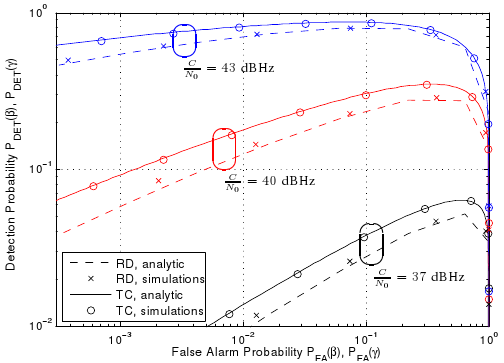
In this work, a comparison between two widespread global navigation satellite system acquisition strategies is presented. The first strategy bases (TC) its decision on comparing the energy within a cell of the partitioned search space to a threshold, while the second one uses the ratio between the two largest cell energies (RD). It is shown that the TC outperforms RD in terms of receiver operating characteristics in many practically relevant cases. Moreover, despite the purported simplicity of the ratio detection method, it is further shown that its complexity is comparable to or even higher than the one of threshold comparison with adaptive threshold setting. The figure shows the receiver operating characteristics (i.e., detection probability as a function of the false alarm probability) for different values of the carrier-to-noise-PSD ratio. The search space consists of 17 possible Doppler frequencies with each 2046 possible code phases. One can easily see that TC...
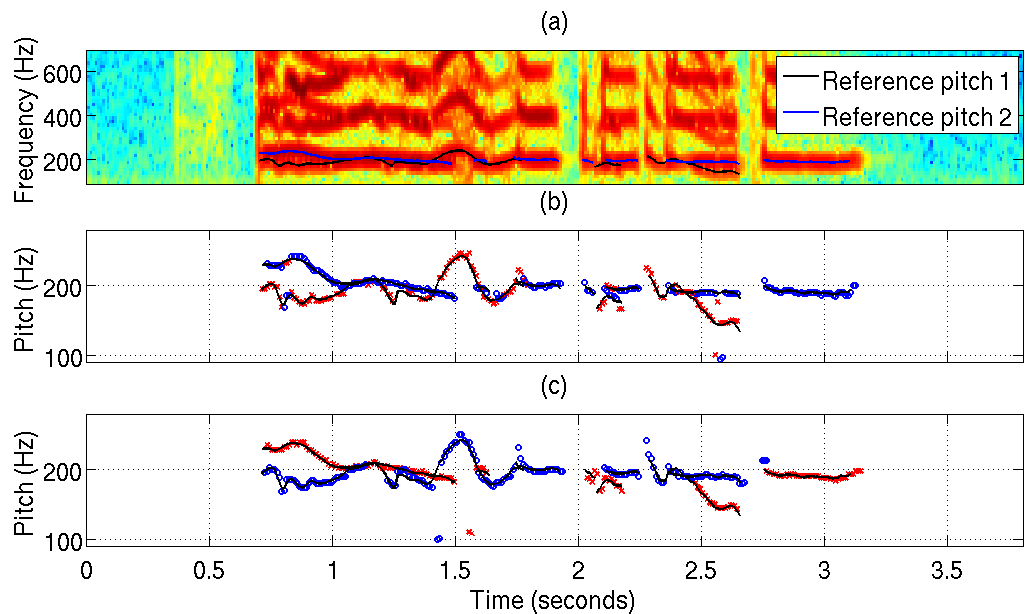
The fundamental frequency is an important characteristic of speech signals. Most energy of voiced speech utterances is carried by the harmonics, which are located at integer multiples of the fundamental frequency. The task of multipitch tracking is to extract the fundamental frequency from a mixture of simultaneous speakers. In this work, we investigate a model based approach where speaker specific characteristics are learned beforehand. The availability of speaker dependent (SD) models allows to additionally assign a pitch estimate to its corresponding speaker. The above figure shows an example for the speech mixture of two female speakers. Panel (a): Spectrogram of speech mixture, together with reference pitch trajectories extracted from single speech recording (black and blue line). Note that the pitch trajectories of both speakers are located in the same frequency range crossing each other. In this situation, the assignment of pitch estimates to corresponding speakers based on time-continuity constraints is...
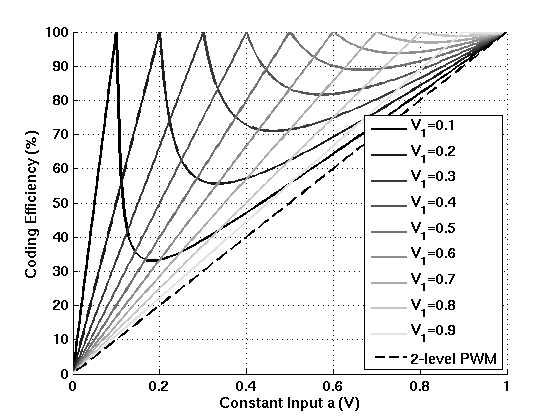
In modern wireless communication systems, complex modulation techniques are employed for increased data rates and spectral efficiency. However, conventional radio frequency (RF) transmitters with linear power amplifier operation only provide moderate overall transmitter efficiency for complex modulated signals. Switched-mode power amplifiers (SMPA) with appropriate baseband modulation techniques such as pulse-width modulation (PWM) are employed to increase the overall transmitter efficiency. One of the drawbacks of this technique is out-of-band power. This out-of-band power needs to be filtered in order to fulfill the transmission spectrum requirements, thus reducing the overall efficiency. A measure for the efficiency degradation of such pulsed transmitters is the coding efficiency. This work investigated optimization concept on the coding efficiency for multilevel pulsed transmitters. The figure above illustrates the comparison of coding efficiency curves between the optimized multilevel and the two-level pulsed transmitters for constant input signals. As shown, all solid curves (optimized) are better than the...
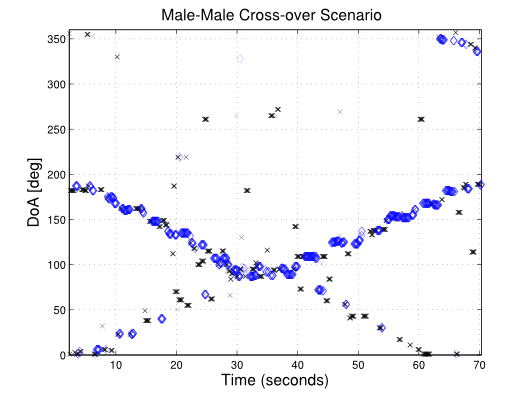
With increasingly powerful and affordable computational resources for digital signal processing and growing use of sensor arrays, acoustic source localization has become an interesting area of research. In contrast to traditional localization applications such as radar and sonar, speech source localization introduces additional challenges due to the wideband and non-stationary nature of speech signals, due to the unknown trajectories of the speakers and due to the effects of multipath propagation in enclosures. In our work, we make use of fundamental frequency or pitch information of speech signals in addition to the location . Our “position-pitch”-based algorithm pre-processes the speech signals by a multiband gammatone filterbank that is inspired from the auditory model of the human inner ear. Moreover, our method incorporates the study of the human neural system use of correlations between adjacent sub-band frequencies and grouping of spectro-temporal regions formed by fundamental frequency cues. The algorithm is able to...
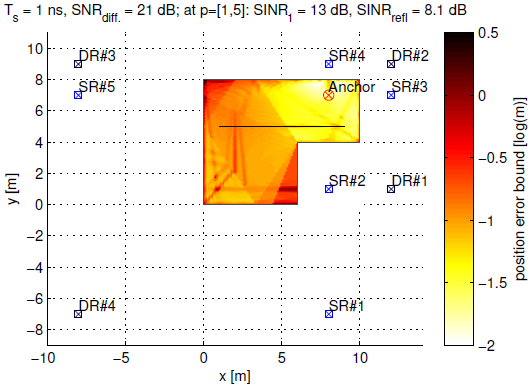
Indoor positioning based on ultra-wideband radio signals remains a challenging problem, in particular due to error induced by non-line-of-sight propagation conditions. The MINT (multipath-aided indoor navigation and tracking) approach exploits the geometry of deterministic multipath components (MPCs) in such situations. Reflected multipath components are accounted for by virtual signal sources, indicated as “SR” and “DR” in the figure. The figure shows the Cramèr-Rao lower bound of the position error for this scenario. The bound has been derived from a channel model, where diffuse multipath is represented as a colored Gaussian process that influences the effective SNR of deterministic MPCs. The adverse effect of path overlap is seen. Computational results and analysis show a three-fold importance of a large signal bandwidth: The bandwidth reciprocal (i.e. the pulse duration) multiplies the error standard deviation - a fundamental result well-known from AWGN channels. But it also multiplies the effective power of the interfering...
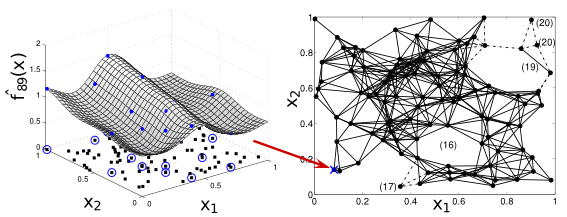
In this work, a fully decentralized algorithm which is inspired by sparse Bayesian learning (SBL) is presented. It can be used for non-parametric sparse estimation of unknown spatial functions -spatial fields- with wireless sensor networks (WSNs). Such a field is represented as a linear combination of weighted fixed basis functions. The figure shows the estimated field function of one particular sensor. The field function is modeled as a weighted superposition of Gaussian kernels centered at each sensor’s position. The network collaboratively determines which of the kernels are needed, where the centers of the relevant kernels are marked by circles. The solid connection lines depicted on the right represent regions with equivalent sparsity patterns. It can be seen that most of the sensors agree on the same subset of kernels. For more information, please read our paper. By defining a new probabilistic model for distributed SBL that is built of the...
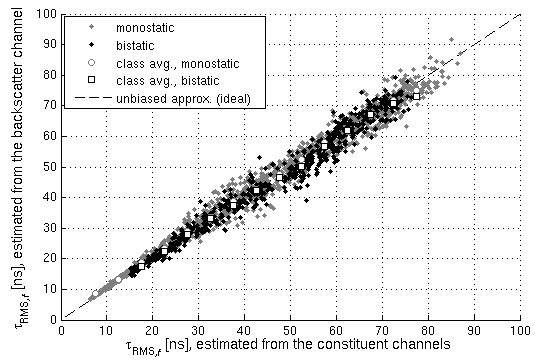
Backscatter systems have become more and more popular since radio-frequency identification (RFID) emerged a few years ago. Recent advances in short-range indoor backscatter localization, however, have shown that there is little to no information available on wideband backscatter channels despite the abundance of analyses available for single-channel links. Instead of presenting backscatter channel analyses, we present a method to calculate wideband backscatter channel characteristics from existing single-channel measurements. The presented method holds for bistatic as well as monostatic antenna setups and will be published in one of the upcoming issues of IEEE Transactions on Antennas and Propagation. The above image shows a comparison between the RMS delay spread calculated from single-channel measurements (x-axis) and the RMS delay spread estimated directly from the corresponding backscatter channel (y-axis). Note that the dots cluster around the dashed line, which means that indeed the RMS delay spread calculated from the single-channel link matches the...
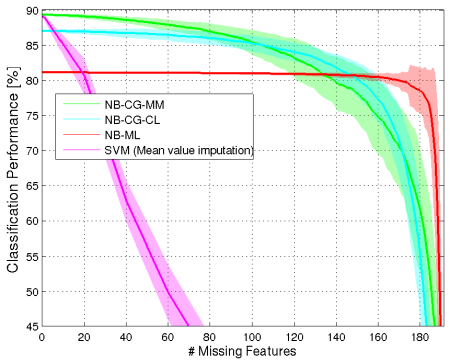
Classification is an important task in machine learning. It deals with assigning a given object to one of a number of different categories. We present a maximum margin parameter learning algorithm for Bayesian network classifiers using a conjugate gradient method for optimization to solve this task. In contrast to previous approaches, we maintain the normalization constraints of the parameters of the Bayesian network during optimization, i.e. the probabilistic interpretation of the model is not lost. This enables to handle missing features in discriminatively optimized Bayesian networks. The potentials of the proposed method as well as a comparison to other existing work on maximum margin Bayesian networks is focus of this work. The above figure illustrates the capability of the presented maximum margin Bayesian network classifiers in dealing with missing features in the Washington D.C. Mall dataset (details on this dataset can be found in the publication). It shows the classification...
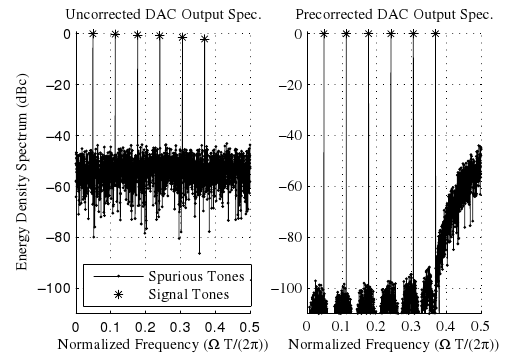
Linear time-varying systems are encountered in many technical areas, for example as a means of modeling communication channels or signal processing blocks. Typically, this time-varying behavior is undesired as it has a negative impact on the performance of consecutive blocks in the signal processing chain. This negative impact can be reduced by either preprocessing or postprocessing the signal with a time-varying correction filter. Methods for the design of these filters are the focus of this work. The viability of a proposed filter design method is demonstrated by preprocessing the digital input signal of a digital-to-analog converter (DAC) which exhibits non-uniform sample-and-hold signals. This non-uniform behavior is caused by sampling jitter and results in a floor of spurious tones reducing the spectral purity of the output signal of the DAC. Employing the proposed precorrection scheme, a considerable attenuation of the in-band spurious tones in the output spectrum can be observed, resulting...
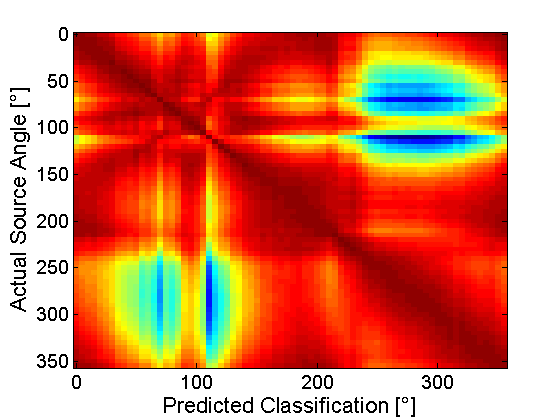
Many known sound localization algorithms are based on processing signals received by multiple, spatially separated sensors, e.g. microphone arrays. The advantages of single-channel sound source estimation are the lower costs for a single microphone and the possibility of developing very small gadgets. In this work we developed an accurate speaker localization strategy in the horizontal plane using the signal of only one microphone. Based on a set of measured head-related transfer functions (HRTFs) from a dummy head and a statistical model of speech, an estimation of the sound direction has been carried out. High-dimensional spectral features (STFT coefficients) are taken and the direction of the sound source is evaluated with Gaussian mixture models (GMMs) using a maximum likelihood (ML) framework. An evaluation of the developed method in a synthetic test environment yields excellent results and leads to a promising approach which can be further investigated in future research. For more...
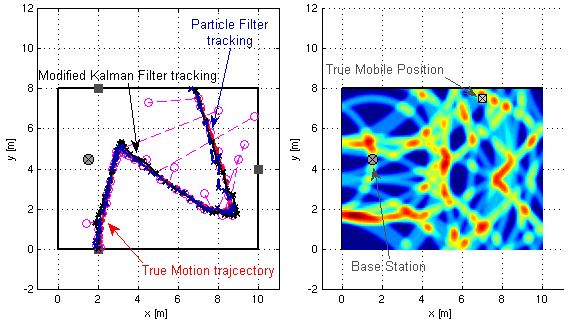
Indoor localization systems have to face very challenging conditions, e.g. dense multipath scenarios resulting from propagation phenomena like reflections and scattering. Recently, our group has proposed a series of robust and accurate tracking algorithms for an ultra-wideband radio-based localization concept that is able to effectively make use of reflected signal components. We reach accuracies on centimeter level at a high level of robustness. For further information, please see our paper at the IPIN 2010!

Left: examples from the ORL face images (http://www.cl.cam.ac.uk/research/dtg/attarchive/facedatabase.html). Right, top: bases extracted using L0-sparse NMF with 10, 25, 33% percent non-zeros pixels. Right, bottom: bases extracted using L1-sparse NMF with corresponding sparseness values (Hoyer, 2004). Nonnegative matrix factorization (NMF) is a popular data mining technique, which typically results into a sparse and part-based representation. To further enhance sparseness, several authors proposed NMF techniques which constrain or penalize the L1-norm of the NMF components, which is known to introduce sparsity. Sparseness measured in terms of L0-pseudo-norm (i.e. number of non-zero pixels) is typically considered as hard problem. In this work, simple but effective approximate techniques for NMF with L0-sparseness constraints are proposed. L0-sparse NMF achieves almost the same reconstruction quality (SNR) as L0-sparse NMF, while being significantly sparser in terms of L0-norm. Further information can be found in the publication!
