Hybrid Generative-Discriminative Training of Gaussian Mixture Models
- Published
- Wed, Aug 01, 2018
- Tags
- rotm
- Contact
Recent work has shown substantial performance improvements of discriminative probabilistic models over their generative counterparts. However, since discriminative models do not capture the input distribution of the data, their use in missing data scenarios is limited. To utilize the advantages of both paradigms, we present an approach to train Gaussian mixture models (GMMs) in a hybrid generative-discriminative way. This is accomplished by optimizing an objective that trades off between a generative likelihood term and either a discriminative conditional likelihood term or a large margin term using stochastic optimization. Our model substantially improves the performance of classical maximum likelihood optimized GMMs while at the same time allowing for both a consistent treatment of missing features by marginalization, and the use of additional unlabeled data in a semi-supervised setting. For the covariance matrices, we employ a diagonal plus low-rank matrix structure to model important correlations while keeping the number of parameters small. We show that a non-diagonal matrix structure is crucial to achieve good performance and that the proposed structure can be utilized to considerably reduce classification time in case of missing features. The capabilities of our model are demonstrated in extensive experiments on real-world data.
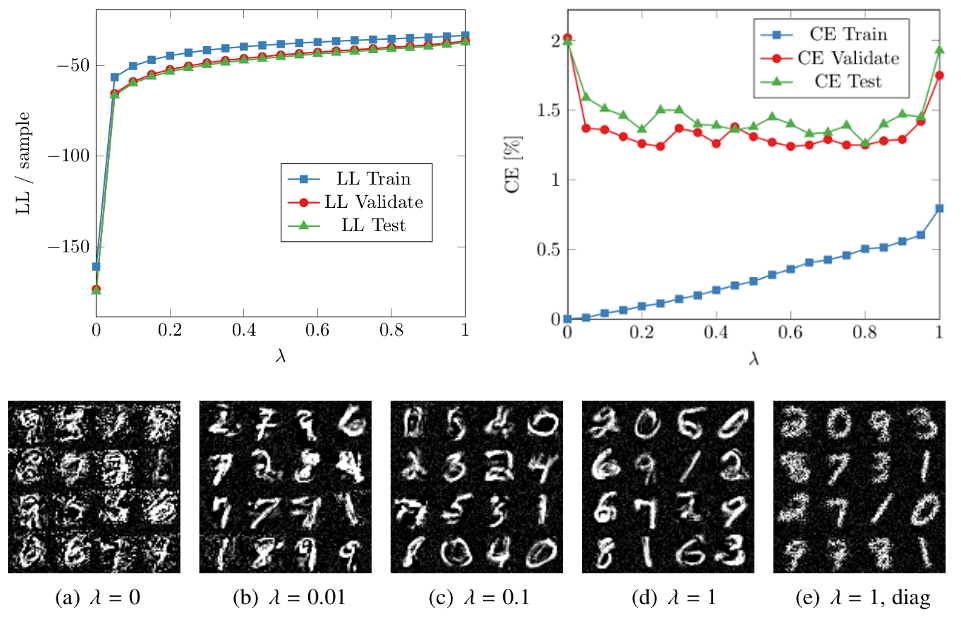
The top figures show how the generative-discriminative trade-off parameter influences the log-likelihood per sample (top left) and the classification error (top right) on MNIST. The log-likelihood shows how well the data is fit and it increases as the trade-off parameter favors the generative aspect of the model. For small values (discriminative), the model overfits the data as there is a small training error but a high validation error. For large values (generative), the model underfits the data as both training error and validation error are high. An intermediate value, where both the generative and discriminative aspects are considered, appears to be just right. The bottom figures show images sampled from hybrid GMMs for several trade-off parameters. The generative characteristics of the model are completely abandoned for discriminative training (a) and the sampled images are hard to identify. As the generative aspect is increased from (b) to (d), the sampled images look more natural. The images in (e) are sampled from a purely generative model with diagonal covariance matrices. The images appear noisy since correlations, causing neighboring pixels to have similar intensities, are not modeled. This shows that modeling correlations is important.
Code for the experiments is available online.
Browse the Results of the Month archive.
