Error Analysis and Precision Estimation for Floating-Point Dot-Products Using Affine Arithmetic
- Published
- Wed, Aug 01, 2012
- Tags
- rotm
- Contact
In this work we use Affine Arithmetic (AA) to estimate the rounding error of different floating-point dot-product implementations. Two floating-point dot-product architectures - a sequential dot-product and a parallel (binary-tree) dot-product - are considered over a wide range of parameters. It is shown that an AA-based probabilistic bounding operator is able to provide a tighter rounding error bound compared to existing techniques. Furthermore, the analytical models for the rounding errors of different floating-point dot-product architectures are derived. As the estimated rounding error bounds are then used for bit width allocation for hardware implementations, the presented error models are key to floating-point code generators and efficient design space exploration.
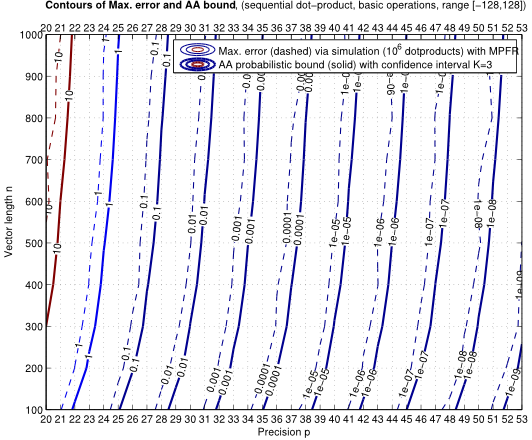
The figure presents the contour maps of the maximum rounding error (dashed lines) obtained by extensive simulations and the AA-based probabilistic rounding error bound (solid lines) of the sequential dot-product. We observe that regardless of the vector length or precision, the AA-based probabilistic bounds are very close to the realistic errors via simulations. For floating-point bit width allocation, this corresponds to an overestimation of up to 1 mantissa bit.
For more information, please refer to our paper!
Browse the Results of the Month archive.
