Capacity and Capacity-Achieving Input Distribution of the Energy Detector
- Published
- Tue, May 01, 2012
- Tags
- rotm
- Contact
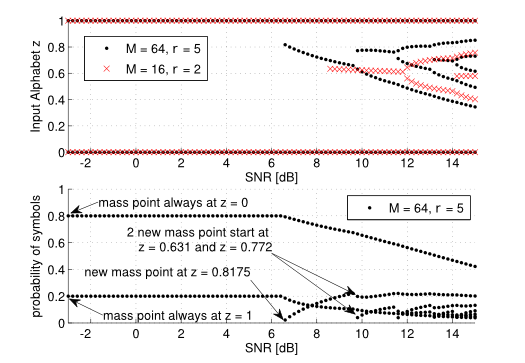
This work presents the channel capacity and capacity-achieving input distribution of an energy detection receiver structure. Using the Blahut-Arimoto algorithm combined with a particle method, the positions and probabilities of the optimal mass points were found. It was shown that the capacity increases with decreasing noise dimensionality M and increasing peak-to-average power ratio (PAPR, parameter r in figure) and that the achieving input distribution is discrete with a finite number of mass points.
The figure shows the positions and probabilities of the mass points of the capacity-achieving input distribution over the SNR for different PAPR and noise dimensionality M. The average and peak power are constraints to the transmitted modulation alphabet and the noise dimensionality M is the product of the integration time and the receiver bandwidth of the energy detector.
The simulation results have shown that the optimal input distribution, if an AP and PA constraint are applied, is always discrete with a finite number of mass points and that always mass points at zero and maximum amplitude appear. Furthermore, the results point out that for low SNR OOK is always an optimal modulation scheme and for higher SNR values higher-order PAM are optimal.
More details can be found in our paper.
Browse the Results of the Month archive.
