Belief Propagation Accurate Marginals or Accurate Partition Function
- Published
- Thu, Aug 01, 2019
- Tags
- rotm
- Contact
The marginals and the partition function can be estimated in a straight-forward manner for tree-structured models but require efficient approximation methods if the graphical model contains loops. One such method is Belief Propagation (BP) that exploits the structure of probabilistic graphical models in order to approximate the marginal distribution and the partition function.
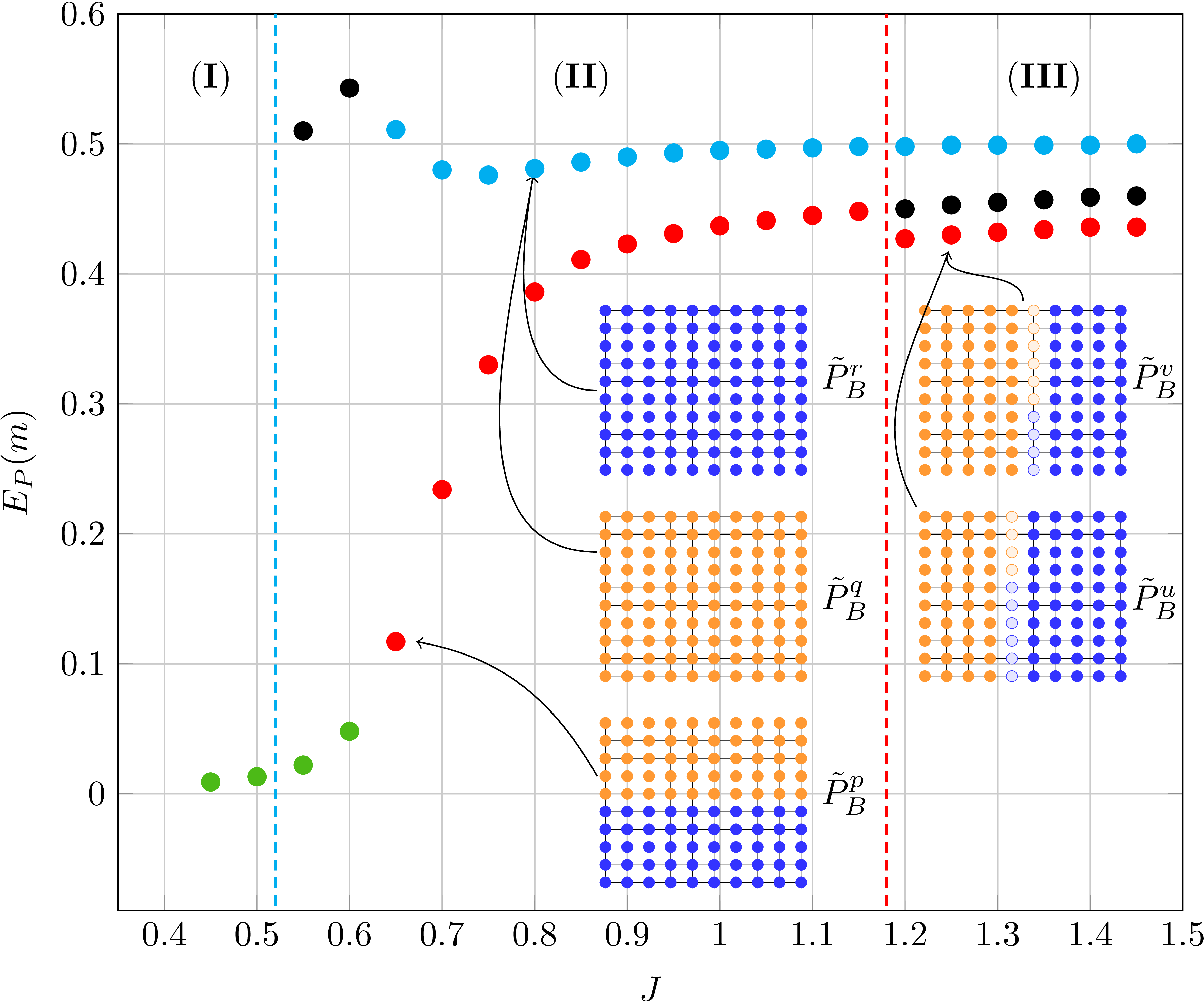
In this work, we analyze the difference between accurate marginals and an accurate partition function. Therefore, we go beyond well-established models (e.g., attractive models with identical or random potentials) and introduce a rich class of attractive models with inherent structure: patch potential models. These models exhibit many interesting phenomena and provide deep insights into the relationship between the approximation quality of the marginals and the partition function.
We discuss the properties of the solution space and demonstrate that: (i) three different regions with fundamentally different properties exist; (ii) although it is often infeasible to obtain and combine all fixed points, there exists one region which allows us to do so; (iii) we observe that no principle relationship exists between the approximation quality of the marginals and the partition function and present fixed points that provide the most accurate Bethe partition function but not the most accurate marginals.
Figure: Accuracy of the marginals for an exemplary model. We emphasize the fixed points providing the most accurate marginals in red, the fixed point providing the most accurate partition function in blue, and the fixed point optimal with respect to both quantities in green.
More information can be found in our paper and supplements.
Browse the Results of the Month archive.
