Bayesian Learning of Sum-Product Networks
- Published
- Sun, Dec 01, 2019
- Tags
- rotm
- Contact
Sum-product networks (SPNs) are flexible density estimators and have received significant attention, due to their attractive inference properties. While parameter learning in SPNs is well developed, structure learning leaves something to be desired: Even though there is a plethora of SPN structure learners, most of them are somewhat ad-hoc, and based on intuition rather than a clear learning principle.
In this paper, we introduce a well-principled Bayesian framework for SPN structure learning. First, we decompose the problem into i) laying out a basic computational graph, and ii) learning the so-called scope function over the graph. The first is rather unproblematic and akin to neural network architecture validation. The second characterises the effective structure of the SPN and needs to respect the usual structural constraints in SPN, i.e.~completeness and decomposability. While representing and learning the scope function is rather involved in general, in this paper, we propose a natural parametrisation for an important and widely used special case of SPNs. These structural parameters are incorporated into a Bayesian model, such that simultaneous structure and parameter learning is cast into monolithic Bayesian posterior inference.
In various experiments, our Bayesian SPNs often improve test likelihoods over greedy SPN learners. Further, since the Bayesian framework protects against overfitting, we are able to evaluate hyper-parameters directly on the Bayesian model score, waiving the need for a separate validation set, which is especially beneficial in low data regimes. Bayesian SPNs can be applied to heterogeneous domains and can easily be extended to nonparametric formulations. Moreover, our Bayesian approach is the first which consistently and robustly learns SPN structures under missing data.
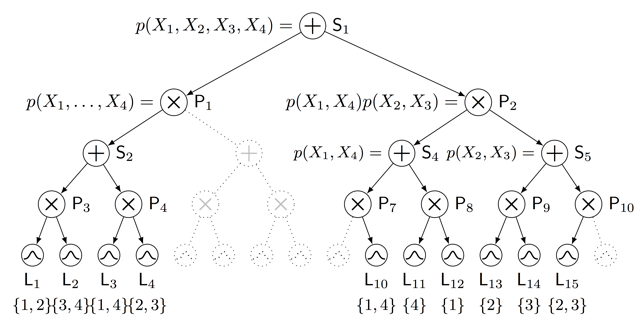
Figure: An example of a computational graph and a sum-product-network (SPN) structure, defined by a scope function, discovered using posterior inference. The resulting SPN contains only a subset of the nodes in the graph as some sub-trees die out during inference (dotted).
More information can be found in our paper.
Browse the Results of the Month archive.
