Markov Aggregation and Information Bottlenecks
- Published
- Tue, Apr 01, 2014
- Tags
- rotm
- Contact
Many scientific disciplines, such as systems biology or natural language processing, suffer from Markov chains with exploding state spaces. Markov aggregation, i.e., finding a Markov chain on the partition of the original state space, is one way to reduce the computational complexity of the model. We provide an information-theoretic cost function for the problem of Markov aggregation and show that the information bottleneck method, a popular technique in machine learning, can be used to find a solution iteratively.
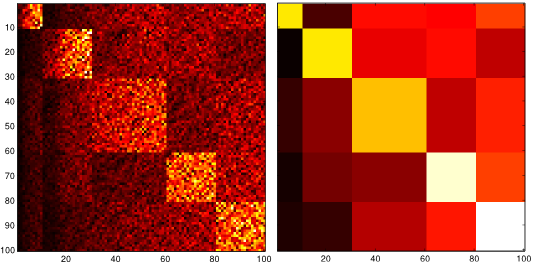
The cost function we use is an upper bound on the Kullback-Leibler divergence rate between the aggregated Markov chain and the stationary process obtained by projecting the original Markov chain through the partition function. The latter is not Markov in general; if it is, the original chain is called lumpable w.r.t. the partition function. By defining the cost function appropriately, it can be shown that the solution is closely related to lumpability and that, by relaxing the problem, the cost function is minimized by the information bottleneck method. The figure shows the transition matrix of a 100-state Markov chain together with its aggregation, which was obtained using the agglomerative information bottleneck method. As it can be seen, the strongly interacting sets of states were identified successfully.
If you want to know more about this joint work with Tatjana Petrov and Heinz Koeppl from ETH Zurich, please take a look at our paper (currently under review for the IEEE Transactions of Automatic Control)!
Browse the Results of the Month archive.
