On Loopy Belief Propagation -- Local Stability Analysis for Non-Vanishing Fields
- Published
- Sun, Oct 01, 2017
- Tags
- rotm
- Contact
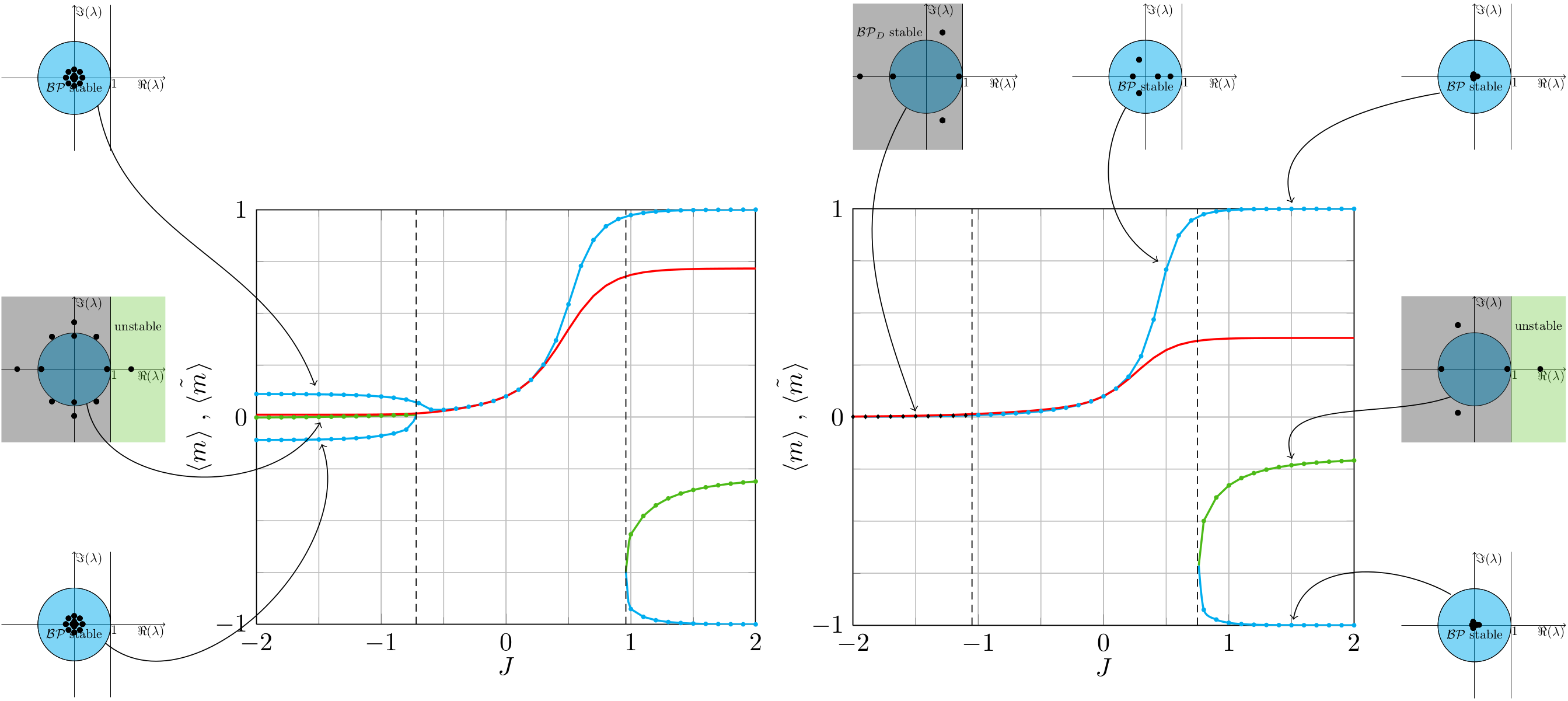
In this work, we obtain all fixed points of belief propagation and perform a local stability analysis. We consider pairwise interactions of binary random variables and investigate the influence of non-vanishing fields and finite-size graphs on the performance of belief propagation; local stability is heavily influenced by these properties. We show why non-vanishing fields help to achieve convergence and increase the accuracy of belief propagation. We further explain the close connections between the underlying graph structure, the existence of multiple solutions, and the capability of belief propagation (with damping) to converge. Finally, we provide insights into why finite-size graphs behave better than infinite-size graphs.
The figures show all stationary points of belief propagation for grid graphs and fully connected graphs. The exact solution is depicted in red and approximate solutions are shown in blue (stable), black (stable with damping), and green (unstable).
More information can be found in our paper.
Browse the Results of the Month archive.
