Fixed Points of Belief Propagation
- Published
- Sun, Jan 01, 2017
- Tags
- rotm
- Contact
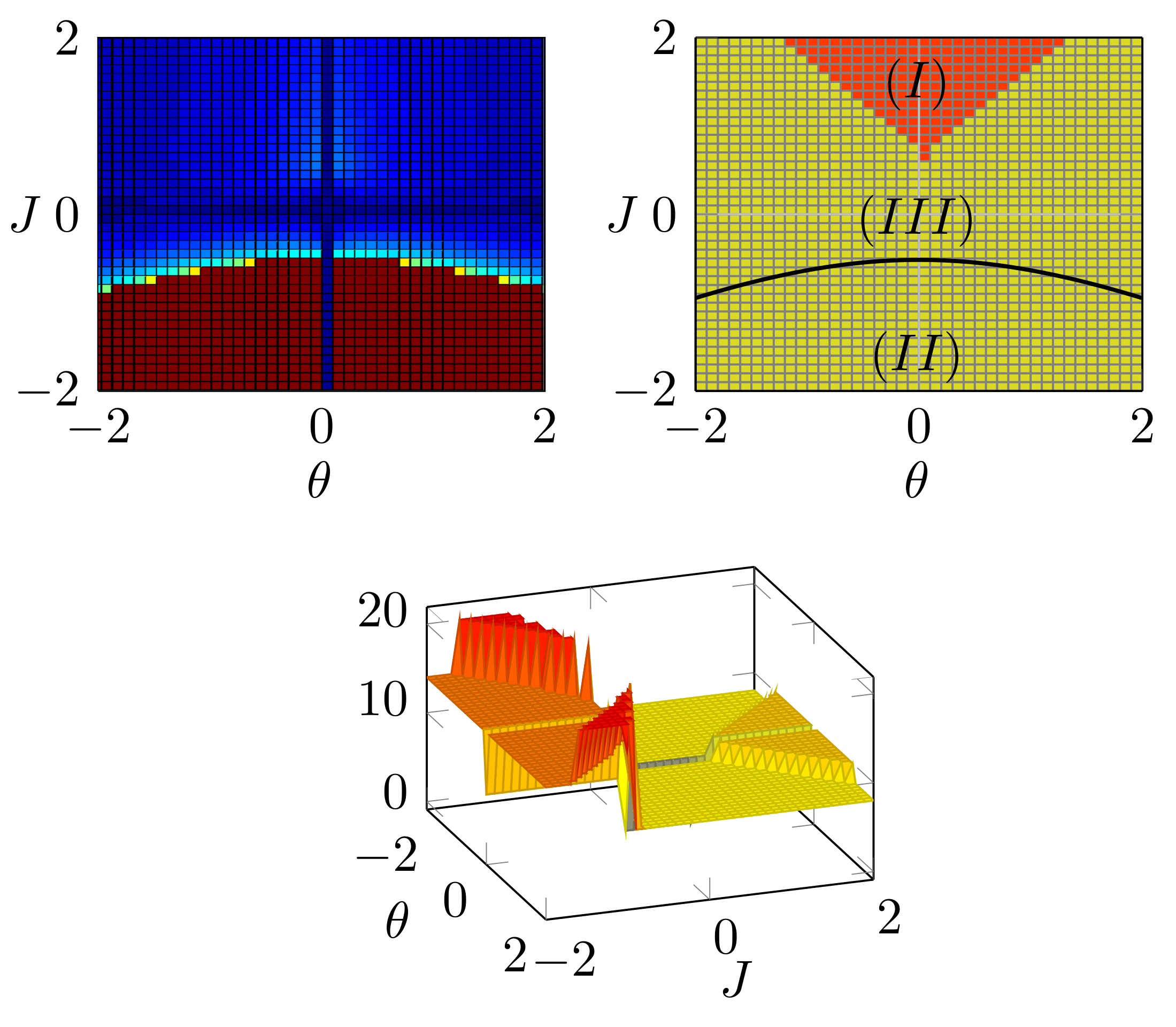
Belief propagation is an iterative method to perform approximate inference on arbitrary graphical models. Whether it converges and if the solution is a unique fixed point depends on both, the structure and the parametrization of the model. To understand this dependence it is interesting to find all fixed points.
We formulate a set of polynomial equations, the solutions of which correspond to BP fixed points. Experiments on binary Ising models show how our method is capable of obtaining all fixed points.
The figure on the upper-left-hand-side shows the number of iterations until belief propagation converged – for red it did not converge at all. The upper-right-hand-figure shows the number of fixed points (yellow: unique fixed point, red: three fixed points). Phase transitions separate the parameter space into three distinct regions. In the lower figure the number of real solutions is depicted: at the onset of phase transitions a sudden increase in the number of real solutions can be seen.
For more information, see our recent NIPS (workshop) paper.
Browse the Results of the Month archive.
