How PINNs cheat: Predicting chaotic motion of a double pendulum
- Published
- Thu, Jun 01, 2023
- Tags
- rotm
- Contact
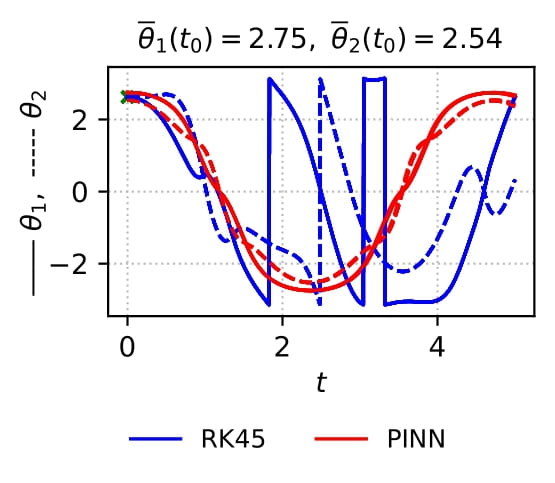
Physics-informed neural networks are a deep learning approach to solving differential equations given only information about the initial and boundary conditions. PINNs are easy to implement and have many desirable properties, such as being mesh-free. Unfortunately, it has been shown that training PINNs is not so straightforward - convergence problems often arise when simulating dynamical systems with high-frequency components, chaotic or turbulent behavior. In this work, we have focused on understanding the underlying reasons for the difficulties in training PINNs by performing experiments on the double pendulum. Our results show that PINNs are not sensitive to perturbations in the initial condition. Instead, the PINN optimization consistently converges to physically correct solutions that only marginally violate the initial condition, but diverge significantly from the desired solution due to the chaotic nature of the system. We hypothesize that the PINNs “cheat” by shifting the initial conditions to values that correspond to physically correct solutions that are easier to learn. Initial experiments suggest that domain decomposition, combined with an appropriate loss weighting scheme, mitigates this effect and allows convergence to the desired solution.
This work has been presented at the NeurIPS workshop “The Symbiosis of Deep Learning and Differential Equations II”. If you are interested have a look here.
Browse the Results of the Month archive.
