Differentiable TAN Structure Learning for Bayesian Network Classifiers
- Published
- Fri, Jan 01, 2021
- Tags
- rotm
- Contact
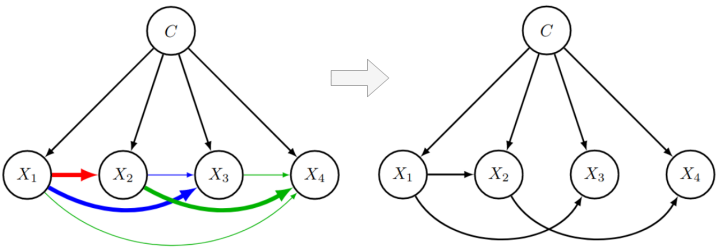
Learning the structure of Bayesian networks is a difficult combinatorial optimization problem. In this paper, we consider learning of tree-augmented naive Bayes (TAN) structures for Bayesian network classifiers with discrete input features. Instead of performing a combinatorial optimization over the space of possible graph structures, the proposed method learns a distribution over graph structures. After training, we select the most probable structure of this distribution. This allows for a joint training of the Bayesian network parameters along with its TAN structure using gradient-based optimization. The proposed method is agnostic to the specific loss and only requires that it is differentiable. We perform extensive experiments using a hybrid generative-discriminative loss based on the discriminative probabilistic margin. Our method consistently outperforms random TAN structures and Chow-Liu TAN structures.
The paper was presented at the International Conference on Probabilistic Graphical Models (PGM 2020) and can be found at https://arxiv.org/abs/2008.09566. Code for the experiments is available at https://github.com/wroth8/bnc.
Figure: Left: Our method learns a distribution over the graph structure. Connections that are more probable are drawn bold. Right: After training, we select the most probable structure, i.e., we select the most probable parent of each node.
Browse the Results of the Month archive.
