Training Discrete-Valued Neural Networks with Sign Activations Using Weight Distributions
- Published
- Tue, Oct 01, 2019
- Tags
- rotm
- Contact
Since resource-constrained devices hardly benefit from the trend towards ever-increasing neural network (NN) structures, there is growing interest in designing more hardware-friendly NNs. In this paper, we consider the training of NNs with discrete-valued weights and sign activation functions that can be implemented more efficiently in terms of inference speed, memory requirements, and power consumption. We build on the framework of probabilistic forward propagations using the local reparameterization trick, where instead of training a single set of NN weights we rather train a distribution over these weights. Using this approach, we can perform gradient-based learning by optimizing the continuous distribution parameters over discrete weights while at the same time perform backpropagation through the sign activation. In our experiments, we investigate the influence of the number of weights on the classification performance on several benchmark datasets, and we show that our method achieves state-of-the-art performance.
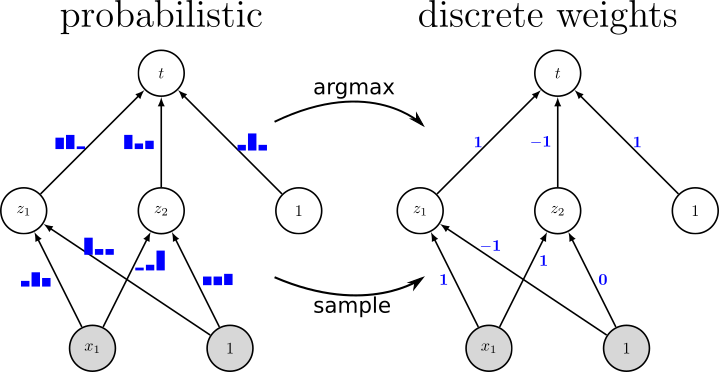
Figure: Instead of learning conventional real-valued weights, we learn a distribution over discrete weights. This is illustrated on the left side of the figure where we learn for each connection of the NN a distribution over ternary weights, i.e., we train the probabilities of three possible weights {-1, 0, +1}. After training has finished, a resource-efficient discrete-valued neural network as shown on the right side of the figure is obtained either by taking the maximum or by sampling from these distributions, respectively.
More information can be found in our paper. Code is available online at http://github.com/wroth8/nn-discrete.
Browse the Results of the Month archive.
