PhD Theses
Prosody has many functions in speech; e.g., cueing information structure (“Max bought a HOUSE.” vs. “MAX bought a house.”), sentence type (“Max bought a house?”), or communicative functions such as turn management (do I want to continue telling you about Max’s new house or am I done talking). This thesis investigates the prosody of yet another kind of communicative function, the expression of attitude (also called stance-taking, evaluation).
As the size and complexity of future accelerators increases, the automated analysis and validation of machine protection functionalities will become more and more critical. The development of a fully automated analysis tool to classify machine-protection-relevant data in the LHC will serve as proof-of-concept for future high energy colliders. It will allow to identify important design requirements which are relevant for the early design phase of such a collider.
Few topics in science and philosophy have been as controversial as the nature of causality. Interestingly, the discussion becomes relatively benign, from a philosophical perspective, as soon as one agrees on a well-defined mathematical model of causality, such as Pearl’s structural causal model (SCM). Assuming that the data comes from some model within a considered class of SCMs, causal questions reduce, in principle, to epistemic questions, i.e., questions about what and how much is known about the model.
Cement kilns, crucial components in the production of cement, are lined with specialized heat-resistant bricks designed to withstand extreme temperatures and harsh conditions. Over time, these bricks gradually wear down due to the constant exposure to high heat and abrasive materials, necessitating periodic inspection and replacement to maintain the kiln’s efficiency and safety.
This dissertation project explores the cochlea’s intricate and nonlinear mechanisms, a crucial component of the human auditory system. The goal is to develop advanced models that represent these biological processes with greater precision and enhance our understanding of their complexities. The human auditory system exhibits notable nonlinear characteristics in various dimensions, including temporal resolution, frequency resolution, and dynamic amplification. Despite its significance, the underlying nature of this nonlinearity remains poorly understood, which has resulted in models that only capture these features qualitatively. By delving deeper into this area, the research aims to bridge the knowledge gap and contribute to creating more accurate and comprehensive representations of the cochlear function.
A multitude of physical phenomena are governed by partial differential equations, and the need to solve these equations quickly and reliably arises in both research and industry. Although state-of-the-art numerical discretisation methods are widely used, significant challenges such as sensitivity to noisy data, high computational cost, and the complexity of mesh generation remain. Machine learning has achieved remarkable success in various domains, but training deep neural networks often requires substantial amounts of data, which are often scarce or expensive to generate for real-world physical systems. Physics-informed machine learning offers a promising alternative by embedding physical laws into the learning process, thereby potentially reducing data requirements. In this thesis, we aim to enhance physics-informed machine learning methods by improving their trainability, enhancing robustness, and incorporating uncertainty quantification.
Upon asking what kind of problems hearing aid users have when listening to music, most of the answers will be that some instruments are too loud, some too soft, or that it is all one big mush. The field of musical scene analysis (MSA) investigates the human perceptual ability to organize complex musical structures, such as the sound mixtures of an orchestra, into meaningful lines or streams from its individual instruments or sections. Many studies have already been performed on various MSA-tasks for humans as it bears the key to better understand music perception and help improve the enjoyment of music in hearing impaired people.
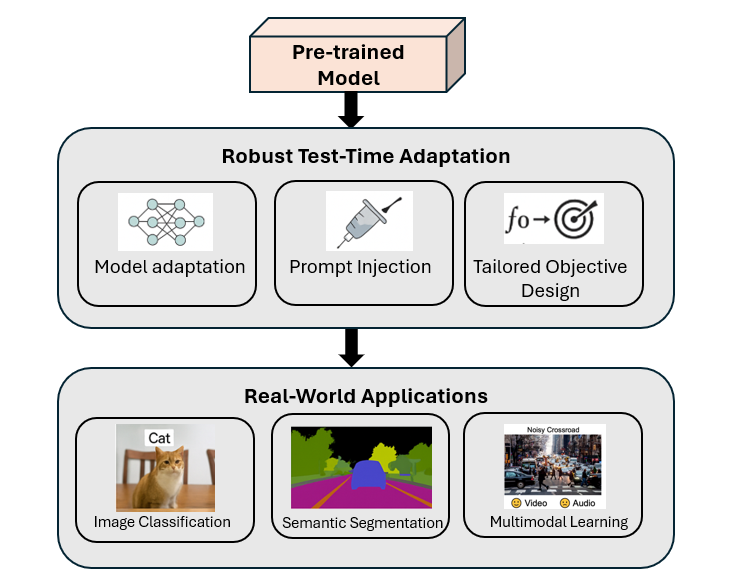
In real-world applications of deep learning, distributional shifts between training and test data can significantly degrade model performance—particularly in tasks such as image classification, semantic segmentation, and multimodal perception. This doctoral thesis explores robust Test-Time Adaptation (TTA) strategies designed to dynamically adapt models during inference, without access to source data or labels.
Successful medical conversations need practice. In medical education, students practice medical conversations with trained actors, who learn their role with the help of scripts with realistic patient histories. Given restricted resources, the number of training opportunities available during medical education is limited. This PhD thesis explores how social robots can support the training of students in conducting medical conversations. Specifically, it explores how automatic speech processing technologies can identify and model aspects of effective medical interactions.

As machine learning models are increasingly deployed in safety-critical and industrial applications, the need for reliable uncertainty estimation alongside predictions becomes essential. Uncertainty estimates not only foster trust in model outputs but also support downstream tasks such as active learning and out-of-distribution detection.
Voice plays a fundamental role in human communication, not only serving a functional purpose but also shaping personal identity and social interaction. Voice disorders, such as dysphonia or conditions resulting from laryngeal cancer, can severely impact the ability to communicate, often leading to social isolation and psychological burdens. In cases requiring a laryngectomy, patients rely on electro-larynx (EL) devices, which generate unnatural, robotic speech that hinders effective interaction. This research explores the potential of voice conversion (VC) models to enhance speech quality for individuals with pathological voices, bridging the gap between assistive technology and natural communication.
Finished Theses
- 2025: Analysis of Message Passing Algorithms and Free Energy Approximations in Probabilistic Graphical Models — Harald Leisenberger
- 2025: (When) Does it Harm to Be Incomplete? Comparing Human and Automatic Speech Recognition of Syntactically Disfluent Utterances — Saskia Wepner
- 2025: Interference Mitigation for Automotive Radar — Mate Andras Toth
- 2025: What's so complex about conversational speech? Prosodic prominence and speech recognition challenges — Julian Linke
- 2024: Using UWB Radar to Detect Life Presence Inside a Vehicle — Jakob Möderl
- 2023: Interpretable Fault Prediction for CERN Energy Frontier Colliders — Christoph Obermair
- 2023: Adaptive Digital Predistortion of Nonlinear Systems — Johann Oliver Steinecker
- 2022: Narrowband positioning exploiting massive cooperation and mapping — Lukas Wielandner
- 2022: Robust Positioning in Ultra-Wideband Off-Body Channels — Thomas Wilding
- 2022: Improving Efficiency and Generalization in Deep Learning Models for Industrial Applications — Alexander Fuchs
- 2022: Deep Learning for Resource-Constrained Radar Systems — Johanna Rock
- 2022: Robust Lung Sound and Acoustic Scene Classification — Truc Nguyen
- 2021: Probabilistic Methods for Resource Efficiency in Machine Learning — Wolfgang Roth
- 2021: Towards the Evolution of Neural Acoustic Beamformers — Lukas Pfeifenberger
- 2021: Signal Processing for Localization and Environment Mapping — Michael Rath
- 2020: Evaluating the decay of sound — Jamilla Balint
- 2020: Cognitive MIMO Radar for RFID Localization — Stefan Grebien
- 2020: Sum-Product Networks for Complex Modelling Scenarios — Martin Trapp
- 2019: Understanding the Behavior of Belief Propagation — Christian Knoll
- 2019: Speech Enhancement Using Deep Neural Beamformers — Matthias Zöhrer
- 2019: A Holistic Approach to Multi-channel Lung Sound Classification — Elmar Messner
- 2019: High-Accuracy Positioning Exploiting Multipath for Reducing the Infrastructure — Josef Kulmer
- 2019: Contributions to Single-Channel Speech Enhancement with a Focus on the Spectral Phase — Johannes Stahl
- 2018: Behavioral Modeling and Digital Predistortion of Radio Frequency Power Amplifiers — Harald Enzinger
- 2017: Measurement Methods for Estimating the Error Vector Magnitude in OFDM Transceivers — Karl Freiberger
- 2017: Localization, Characterization, and Tracking of Harmonic Sources: With Applications to Speech Signal Processing — Hannes Pessentheiner
- 2015: Cognitive Indoor Positioning and Tracking using Multipath Channel Information — Erik Leitinger
- 2015: The Bionic Electro-Larynx Speech System - Challenges, Investigations, and Solutions — Anna Katharina Fuchs
- 2015: Foundations of Sum-Product Networks for Probabilistic Modeling — Robert Peharz
- 2014: Diplophonic Voice: Definitions, models, and detection — Philipp Aichinger
- 2014: Multipath-Assisted Indoor Positioning — Paul Meissner
- 2014: Maximum Margin Bayesian Networks — Sebastian Tschiatschek
- 2014: Signal Processing for Energy-Efficient Burst-Mode RF Transmitters — Shuli Chi
- 2014: Information Loss in Deterministic Systems Connecting Information Theory, Systems Theory, and Signal Processing — Bernhard Geiger
- 2014: Information Loss in Deterministic Systems - Connecting Information Theory, Systems Theory, and Signal Processing — Bernhard Geiger
- 2014: Generalized Noncoherent Ultra-Wideband Receivers — Andreas Pedross-Engel
- 2013: Kernel PCA and Pre-Image Iterations for Speech Enhancemen — Christina Leitner
- 2013: Variational Sparse Bayesian Learning Centralized and Distributed Processing — Thomas Buchgraber
- 2012: Efficient Floating-Point Implementation of Speech Processing Algorithms on Reconfigurable Hardware — Thang Huynh Viet
- 2012: Probabilistic Model-Based Multiple Pitch Tracking of Speech — Michael Wohlmayr
- 2011: Low Complexity Correction Structures for Time-Varying Systems — Michael Soudan
- 2011: Auditory Inspired Methods for Multiple Speaker Localization and Tracking Using a Circular Microphone Array — Tania Habib
- 2011: Tag Localization in Passive UHF RFID — Daniel Arnitz
- 2010: Low-Complexity Localization using Standard-Compliant UWB Signals — Thomas Gigl
- 2010: Adaptive Calibration of Frequency Response MIsmatches in Time-Interleaved Analog-to-Digital Converters — Shahzad Saleem
- 2010: Source-Filter Model Based Single Channel Speech Separation — Michael Stark
- 2010: Phonetic Similarity Matching of Non-Literal Transcripts in Automatic Speech Recognition — Stefan Petrik
- 2009: Signal Processing in Phase-Domain All-Digital Phase-Locked Loops — Stefan Mendel
- 2009: Speech Enhancement for Disordered and Substitution Voices — Martin Hagmüller
- 2009: Adaptive Digital Predistortion of Nonlinear Systems — Li Gan
- 2009: Speech Watermarking and Air Traffic Control — Konrad Hofbauer
- 2008: Low Complexity Ultra-wideband (UWB) Communication Systems in Presence of Multiple-Access Interference — Jimmy Wono Tampubolon Baringbing
- 2008: Modeling and Mitigation of Narrowband Interference for Non-Coherent UWB Systems — Yohannes Alemseged Demessie
- 2008: Signal Processing for Ultra Wideband Transceivers — Christoph Krall
- 2008: UWB Channel Fading Statistics and Transmitted Reference Communication — Jac Romme
- 2007: Variable Delay Speech Communication over Packet-Switched Networks — Muhammad Sarwar Ehsan
- 2007: Semantic Similarity in Automatic Speech Recognition for Meetings — Michael Pucher
- 2007: Wavelet Analysis For Robust Speech Processing and Applications — Van Tuan Pham
- 2006: Multipath Tracking and Prediction for Multiple Input Multiple Output Wireless Channels — Dmytro Shutin
- 2006: Complex Baseband Modeling and Digital Predistortion for Wideband RF Power Amplifiers — Peter Singerl
- 2006: Quality Aspects of Packet-Based Interactive Speech Communication — Florian Hammer
- 2005: Sparse Pulsed Auditory Representations For Speech and Audio Coding — Christian Feldbauer
- 2005: Modeling, Identification, and Compensation of Channel Mismatch Errors in Time-Interleaved Analog-to-Digital Converters — Christian Vogel
- 2005: Digital Enhancement and Multirate Processing Methods for Nonlinear Mixed Signal Systems — David Schwingshackl
- 2004: Nonlinear System Identification for Mixed Signal Processing — Heinz Koeppl
- 2003: Improving automatic speech recognition for pluricentric languages exemplified on varieties of German — ~Micha Baum
- Signal Processing for Burst‐Mode RF Transmitter Architectures — Katharina Hausmair
- Reliable and Robust Localization and Positioning — Alexander Venus
Inactive Theses
- Deep Learning and Structured Prediction — Martin Ratajczak
- Modelling and simulation of porous absorbers in room edges — Eric Kurz
