Published

Fri, Aug 01, 2025

Tags

rotm

Contact

• Bernhard Geiger

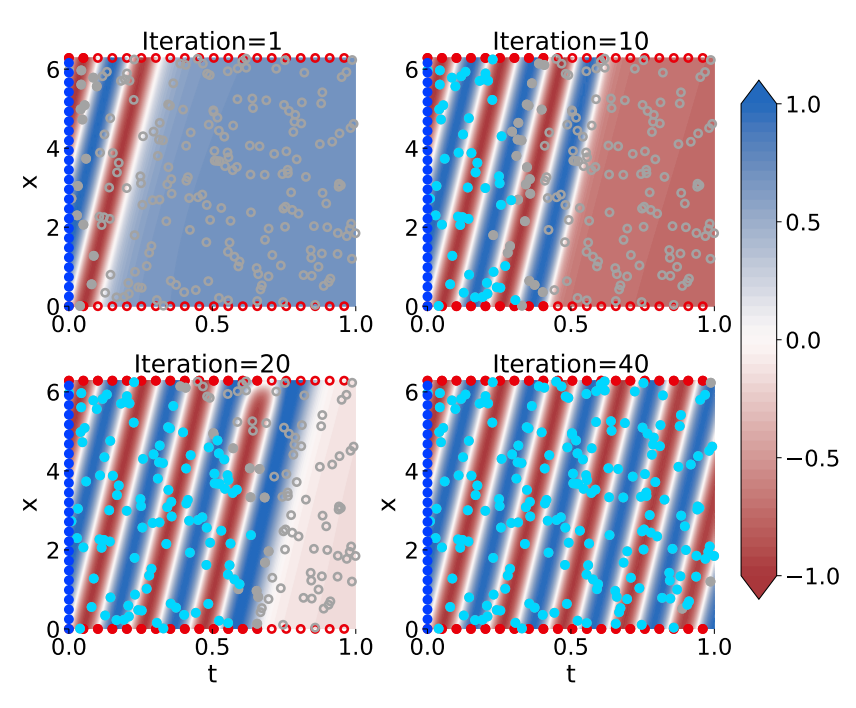
Physics-informed neural networks (PINNs) are known to have poor training convergence if they are used to solve boundary value problems, i.e., if they should learn the solution to a partial differential equation given only initial and boundary conditions. Previous work has shown that training is more stable if the computational domain – the extent of the space and time coordinates for which the PDE should be solved – is small. As a consequence, a series of domain decomposition and collocation point sampling methods were proposed to improve training convergence.

Specifically, Haitsiukevich and Ilin (2023) proposed an ensemble approach that extends the active training domain of each PINN based on i) ensemble consensus and ii) vicinity to (pseudo-)labeled points, thus ensuring that the information from the initial condition successfully propagates to the interior of the computational domain. In this work with Kevin Innerebner and Franz Rohrhofer, we replaced the ensemble by a Bayesian PINN, trained via Hamiltonian Monte Carlo. Ensemble consensus is, consequently, replaced by the variance of the function posterior. The image above shows the solution provided by our B-PL-PINN for a convection system, for different iterations of our algorithm. Data instances for the initial condition and pseudo labels are shown in dark and light blue, collocation points in the interior and the boundary are shown in gray and red. It can be seen that the active computational domain (as shown by filled points) grows with iterations, and that the solution to the convection system is learned successfully. Experiments show that this mathematically principled approach outperforms the ensemble on a set of benchmark systems at only a modest increase of computational complexity.

The paper was published at the International Joint Conference on Neural Networks – if you are interested have a look at the arXiv preprint here.

Browse the Results of the Month archive.